非交互式零知识证明（上）

Posted 2023-04-03 三金哥爱吃醋

【非交互式零知识证明】（上）

文章目录

• 【非交互式零知识证明】（上）
• • 1.交互式证明系统
  • • 交互式证明系统的定义
    • 通俗解释
  • 2.零知识证明
  • • 零知识证明的定义
    • 通俗解释
  • 3.交互式零知识证明典型应用
  • • （一）图同构问题
    • （二）哈密顿回路问题

在了解非交互式零知识证明之前，首先需要了解非交互式证明系统的概念。那么交互式证明系统和非交互式证明系统有什么区别呢？下面将给出介绍。

1.交互式证明系统

交互式证明系统的定义

对于语言L∈0,1^*，以及一对交互图灵机<P,V>，其中p拥有无限的计算能力，称为证明者，V为概率多项式时间的验证者。如果满足以下条件，称<P,V>为语言L的交互证明系统：

1.完备性（Completeness)：对于任何公共输入x∈L
$$Pr[(P,V)(x)=1|x\in L]\le 1-negl(|x|)$$
2.可靠性（Soundness）：对于任何公共输入x∈L和任何无限计算能力的证明者P^*
$$Pr[(P\ast ,V)(x)=1|x\notin L]\ge 1-negl(|x|)$$
其中，negl(|x|)为一个可忽略函数。

通俗解释

这里，我理解的完备性就是，对于正确的声明，验证者"总是（因为是1减去一个可忽略函数）"接受。也就是说，一个诚实的验证者是能够被一个诚实的证明者用一个真声明来说服。而可靠性指的是，对于错误的声明，验证者"总是"拒绝。也就是说，任何欺骗的证明者都不能够让诚实的验证者相信一个错误的声明。

在计算机复杂性理论中，交互证明系统（Interactive proof system）是一种抽象机器，其将计算建模为两个参与方（证明者和验证者）之间的消息交换。通过交换信息，参与方证明某个声明（x∈L）成立。其中：

证明者（Prover）：拥有无穷的计算能力，且不可信；

验证者（Verifier）：拥有受限的计算能力（概率多项式时间），且诚实。

而交互式就是证明者与验证者之间采用交互的形式来完成证明过程。

交互式证明系统的过程如下：

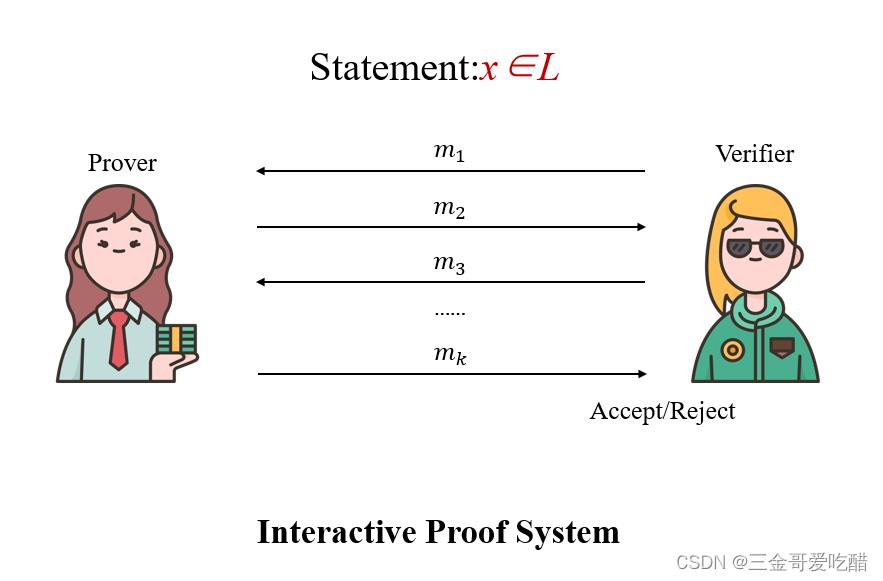
相比之下，传统的数学证明系统是这样的：

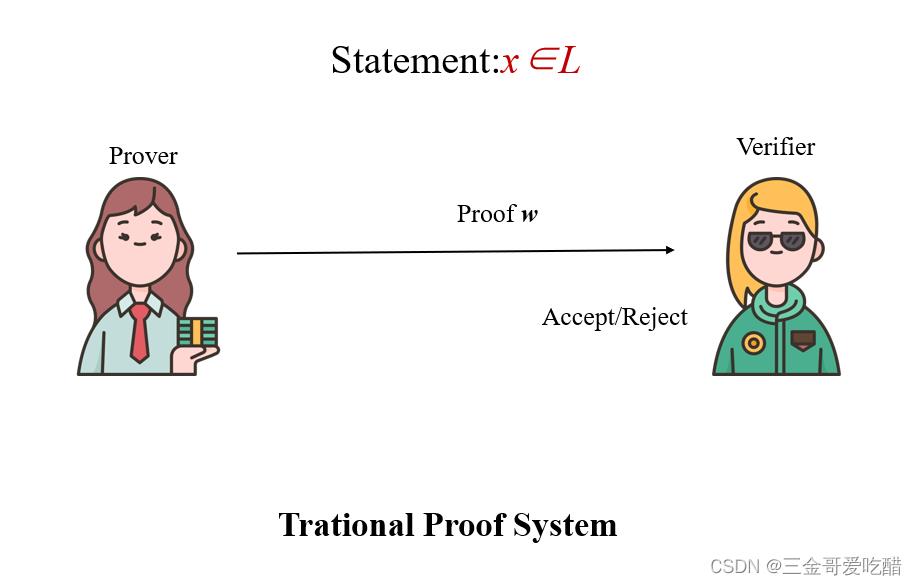
相比而言，传统数学证明存在两个特点：

1.证明是短而简洁的。因为，验证者没有很多精力去读很长的证明。

2.验证者可能获取一些知识。比如证明者所采用的定理、证明的方式等等，一旦验证者获取了证明，那么它也可以向其他人证明。

交互证明系统可以改变上述两个特点，使其能够满足密码学的需求。

2.零知识证明

知道了非交互式证明系统，离我们的非交互式零知识证明又进了一步，下面介绍零知识证明：

零知识证明的定义

对于语言L∈0,1^*，以及一对交互图灵机<P,V>，其中p拥有无限的计算能力，称为证明者，V为概率多项式时间的验证者。如果满足以下条件，称<P,V>为语言L的零知识交互证明系统：

1.完备性（Completeness)：对于任何公共输入x∈L
$$Pr[(P,V)(x)=1|x\in L]\le 1-negl(|x|)$$
2.可靠性（Soundness）：对于任何公共输入x∈L和任何无限计算能力的证明者P^*
$$Pr[(P\ast ,V)(x)=1|x\notin L]\ge 1-negl(|x|)$$
3.零知识性（Zero-knowledge)：对任意概率多项式时间验证者V^*，都存在一个概率多项式时间的模拟器S，使得任意的x∈L，
$$<P,V\ast >(x)\approx cS(x)$$
其中，negl(|x|)为一个可忽略函数，≈_c表示计算不可区分。

通俗解释

简单来说，零知识证明就是：证明者（prover）能够在不向验证者（verifier）提供任何有用的信息的情况下，使验证者（verifier）相信某个论断是正确的。所谓零知识，通俗的来讲，就是既证明了自己想证明的事情，同时透露给验证者的信息为“零”。零知识证明可以分为交互式和非交互式两种。

上述三个性质可以这样理解：

完备性：若断言为真，则验证者总是接受证明；

可靠性：若断言为假，则验证者总是拒绝证明；

零知识：即验证者无法从该证明过程中获取额外的信息。

3.交互式零知识证明典型应用

知道了零知识证明和交互式证明系统之后，我们来看看交互式零知识证明的两个典型应用，然后将与非交互式作出比较。
首先来看一下NP问题中的零知识证明：

（一）图同构问题

图同构（Graph Isomorphism）定义：

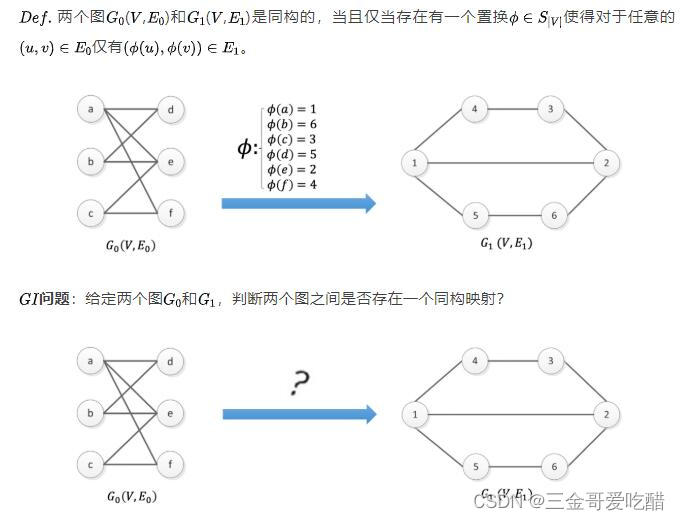
公共输入：两个同构的图G₀（V,E₀）和G₁（V,E₁）。

假设存在一个映射φ使得G₁=φG₀，那么证明者要向验证者证明这一点而不会透露φ的信息，具体的零知识交互证明过程如下：

1.首先，证明者随机产生一个置换π，并计算图H=πG₁，然后证明者将H发送给验证者；

2.然后，验证者随机生成一个比特值α∈_R0,1，并将α发送给证明者；

3.随后，证明者根据α做出不同的相应：

· 如果α=1，证明者发送β=π给验证者；

· 如果α=0，证明者发送β=πφ给验证者；

4.最后，验证者这边计算：

· 如果α=0，那么βG_α=πφG₀=πG₁=H，验证通过；

· 如果α=1，那么βG_α=πG₁=H，验证通过。

我们可以看到，泄露的信息只有π或者πφ，由于π是随机产生的，模拟器可以模拟证明者和验证者之间的交互，并且交互信息和真是交互是计算不可区分的。

（二）哈密顿回路问题

密顿回路的定义：

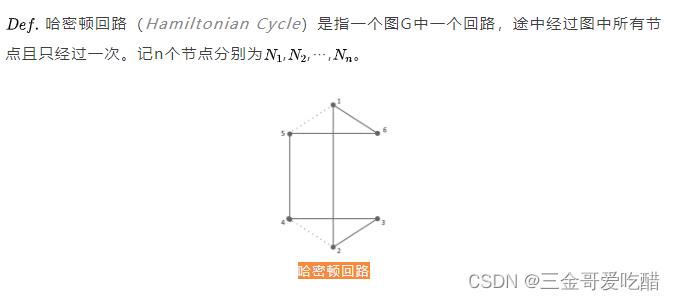
哈密顿难题：给定一个图G，找出该图的一个哈密顿回路。

公共输入：一个无向图G，定点数量为n。

具体的零知识交互证明过程如下图所示：

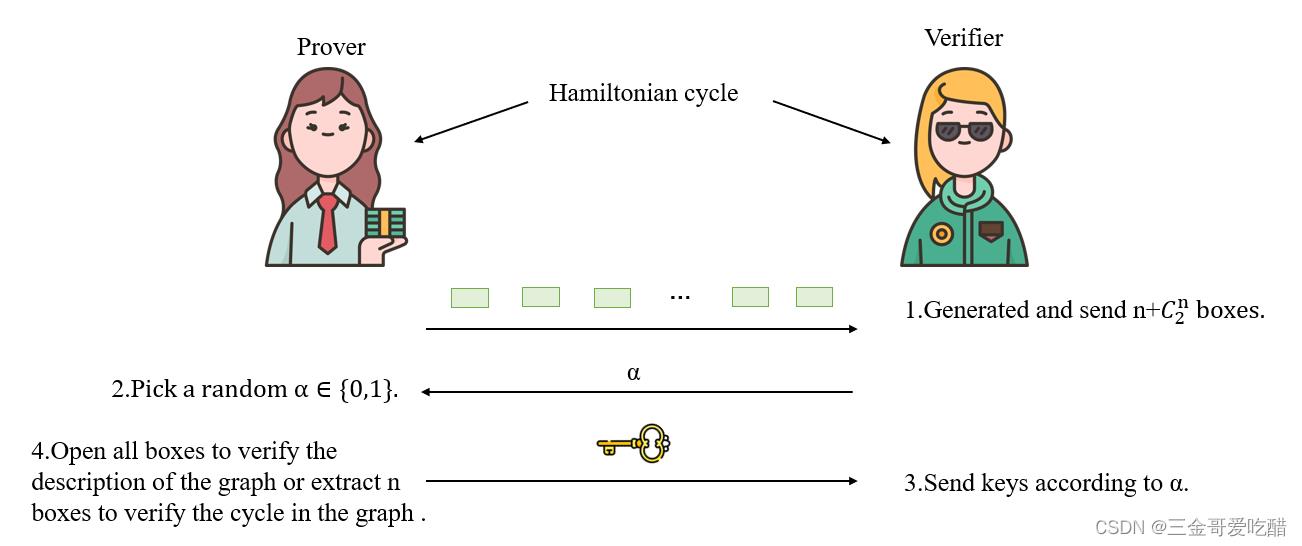
1.首先，证明者随机加密n个定点，即产生一个随机置换将N₁,N₂,…,N_n映射成为B₁,B₂,…B_n；然后设置B_ij的值，如果(Bi,Bj)是一条边，则B_ij=1，否则B_ij=0。证明者将B_i和*B_j放入n+Cⁿ₂*个黑盒中，并发送给验证者；

2.验证者随机生成一个比特值α∈_R0,1，并将α发送给证明者；

3.证明者根据α做出不同的响应：

· 如果α=0，证明者把打开所有黑盒的钥匙和置换都发送给验证者；

· 如果α=1，证明者把打开一个HC回路*(B_ij,B_jk,B_kl,…,B_ti)*的钥匙发送给验证者；

4.验证者根据α做出不同的验证：

· 如果α=0，验证者打开所有的黑盒，并验证其中一个是否是G的同构（上面已经介绍过同构的概念），如果不是，则拒绝；

· 如果α=1，验证者打开指定的黑盒，验证是否所有打开的*B_ij*都是1,。如果不全是，则拒绝。如果未拒绝，进行下一轮证明。

我们可以看到，当α=0时，验证者获取的仅仅是一个G的同构；当α=1时，验证者确实得到了对应图的哈密顿回路，但其中的映射并未透露，所以验证者仍然无法获取G的哈密顿回路，这就是零知识证明。

现在已经get了交互式零知识证明，距离非交互式零知识证明越来越近啦，我们下期再见，敬请期待！

ps：本人也是小菜鸡一枚，有什么不对的地方欢迎批评指正(｀・ω・´)

区块链与密码学第10-12讲：非交互式零知识证明

【本课堂内容全部选编自武汉大学国家网络安全学院教授、博士生导师的《区块链与密码学》授课讲义、教材及互联网，版权归属其原作者所有，如有侵权请立即与我们联系，我们将及时处理。】

10-12非交互式零知识证明

| Fiat-Shamir转换

回顾下Sigma协议，可以发现以下问题：

01Sigma协议的零知识性需要验证者是诚实的

那么，验证者不诚实的话，Sigma协议是否是零知识的？目前，无法说明这个问题。

02Sigma协议的安全基石除了困难问题外，还有什么？

答案是随机挑战。在可靠性分析过程中，可以看出随机挑战值是决定错误概率的关键。

03Sigma协议的效率如何？限制有哪些？

显然，计算量和通信量受限于协议的构造基石（如困难问题、挑战轮数等等）。而且，交互形式的协议限制了它的使用场景。

---

交互式零知识证明

只能够取信于一个验证者

只在某个时刻有效

非交互式零知识证明（NIZK）

可以取信于很多人（甚至所有人）

证明始终有效

---

Fiat-Shamir变换是一种可以将Sigma协议变成非交互证明的技术。它能够让证明者Prover可以通过给验证者Verifier发送一个证明信息即可完成证明(无需交互，无需返回挑战)。

而且，它能把任何一个Simga协议变成一个数字签名，签名的含义就是「知道这个Sigma协议的秘密的人已经签署了这个消息」。Prover能够创造一个证明，然后分发给很多个验证者，验证者可以不必联系Prover即可验证证明有效性。同时零知识也变得容易了，因为验证者或者其他敌手不能做任何事情。

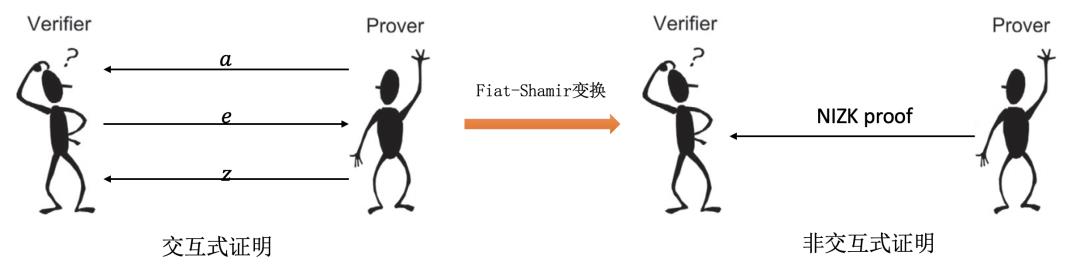
以Schnorr协议为例，如果挑战值e可预知，那么任何人都可以成功欺骗V。

在交互证明时，挑战值可以由验证者V随机产生；

但在非交互证明时，如何保障挑战随机性和不被证明者控制？

为重建信任，Fiat-Shamir转换采用了随机预言机，即让「上帝」来选取挑战值。

问题又来了，真实的随机语言机是不存在。于是，密码学家作出了如下假设：

假设：一个密码学安全的 Hash 函数可以近似地模拟传说中的「随机预言机」。

注意：这个假设无法被证明，所以我们只能信任这个假设，或者说当做一个公理来用。

Hash函数的广义抗碰撞性质决定了它的输出可以模拟随机数，同时在很多情况下（并非所有），对 Hash函数实施攻击难度很高，于是许多的密码学家都在大胆使用。

今天的课程就到这里啦，下节课我们将继续学习非交互式零知识证明，敬请期待！

同学们可以关注点宽学园，每周持续更新区块链系列课程，小宽带你进入区块链世界。我们下节课见啦。

【区块链与密码学】课堂回顾：

区块链与密码学系列文章合集