DFS | 从根到叶的二进制数之和附递归展开图

Posted 2023-04-01 烽起黎明

👉 力扣原题链接

一、思路分析

首先我们来分析一下本题的思路

• 题目说到要求解每一条路径上的结点数字之和，但是本题并不是就简单的累加，而是要结合二进制的知识
• 对于每一条从根到叶的路径都代表一个从最高有效位开始的二进制数，要注意的是这个最高有效位,也就是说越往下走权重越小

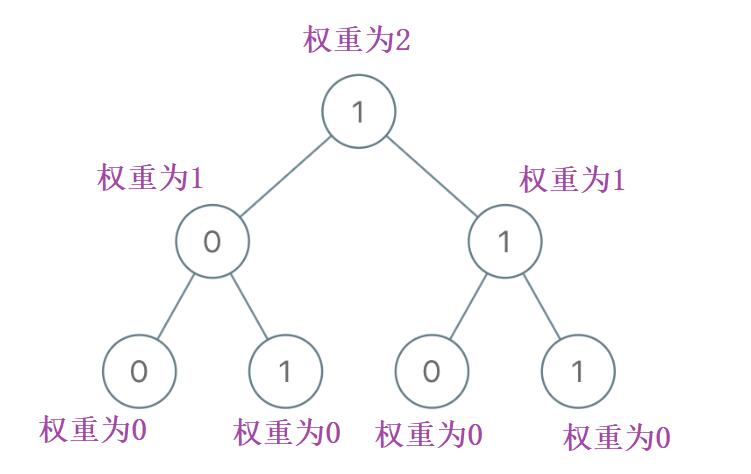
• 首先题目要求要我们求累加和，那么最简单的一个思路就是一个变量res去累加所有的数字之和，但是呢并不是每个结点的路径和都是一样的，所以我们还需要一个变量preSum求出从根结点到当前结点的和
• 因为根节点的权重来得最大，但是我们并不知道这棵树的深度为多少，也就无法确定根节点的权重是否为多少，所以我们要通过【DFS】去遍历这棵树，直到每次碰到叶子结点为止才可以确定从根结点到当前结点的长度，才能得出每一个结点的权重

二、代码详解

有了思路，接下去我们来看看代码该如何书写

根据递归三部曲：

1. 确定递归函数的参数和返回值

• 本题的累加和res我将其定义为成员变量，DFS单独定义为一个成员函数，所以不需要考虑返回值，只要将将根节点传入即可，但是我们还要计算每条路径的和，所以每一层的递归还需一个preSum

2. 确定终止条件

• 对于终止条件，这个很直观，因为一直往下递归，碰到叶子结点就终止回调，所以判断root == NULL即可

3. 确定单层递归的逻辑

• 最后就是单层递归的逻辑，每遍历到一个结点时，我们都需要将当前结点值和从根结点到当前结点的所累加的和preSum进行一个相加，但是又要考虑到二进制权重的问题：
• 因为每一个结点的值均为0或者是1，所以根据二进制上每一位的关系，高一位的权重都比低一位的权重大2倍，所以我们每次在进入当前递归层的时候，都会获取到上一层计算出来的preSum，只需要将其乘2，就可以使上一层的根成为当前层的高一位权重，当然，你也可以使用位运算<< 1
• 若是当前层的根并不是叶子结点的话，就继续递归其左孩子和右孩子，若为叶子结点的话，表示一条路径递归完毕，更新res加上累加后的preSum

以下是整体代码展示💻

 */
class Solution 
private:
    int res = 0;        //累加和作为成员函数
public:
    void DFS(TreeNode* root, int preSum)
    
        if(!root)   return;
        preSum = preSum * 2 + root->val;        //用于单条路径累加和

        if(!root->left && !root->right)
        
            res += preSum;      //若是碰到叶子结点了，就累加次路径的结点和
        

        //递归当前根结点的左右子树
        DFS(root->left, preSum);
        DFS(root->right, preSum);
    
    int sumRootToLeaf(TreeNode* root) 
        DFS(root, 0);
        return res;
    
;

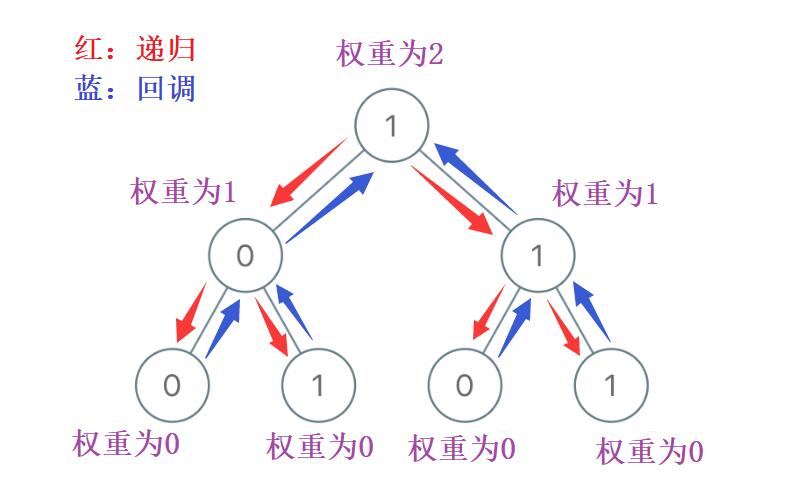
三、算法图解

对于上面的递归部分，我画了【递归展开图】，可以帮助理解，你也可以试着自己画画看😀

以上就是这题力扣1022.从根到叶的二进制数之和相关题解，感谢您的阅读🌹

1022. 从根到叶的二进制数之和

1022. 从根到叶的二进制数之和

• • 题目
  • 算法设计：深度优先搜索

 

---

题目

 

---

算法设计：深度优先搜索

遍历二叉树，沿途不断累加即可。

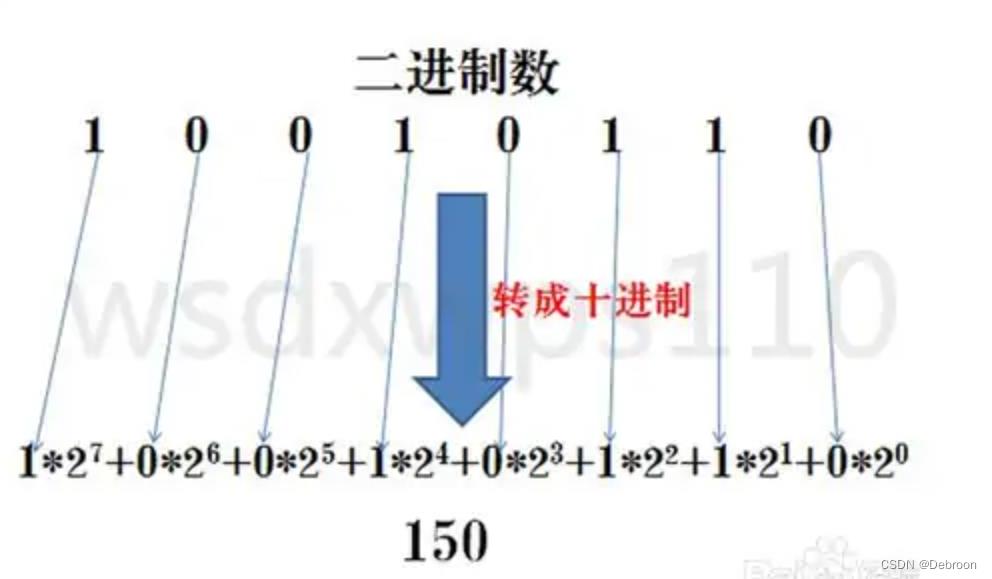
• 二进制转十进制：把二进制数按权展开、相加即得十进制数

class Solution 
public:
    long sum = 0;
    void dfs(TreeNode* &root, long val) 
        if(root == NULL)
            return;
        if(root->left == NULL && root->right == NULL)
            sum += (val*2 + root->val);      // 二进制转十进制：按权展开，再相加
            return;
        
        dfs(root->left, val*2+root->val);  // 二进制转十进制：按权展开，再相加
        dfs(root->right, val*2+root->val); // 二进制转十进制：按权展开，再相加
    
    
    int sumRootToLeaf(TreeNode* root) 
        dfs(root, 0);
        return sum;
    
;