共轭梯度法求解线性方程组python实现

Posted 2022-09-14 咕咕没有梦想

Ax = b

cg方法解方程组，前提是正定对称矩阵哦。

举个例子，求解如下方程组。

 

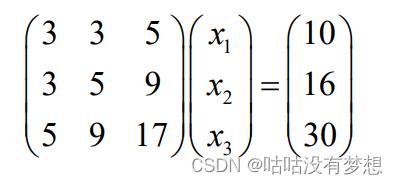
下面是 python代码实现，可推广到任意阶次使用哦，并且迭代n次就会有精确解。

import numpy as np
import pprint

r_list = []
p_list = []
x_list = []
A = np.array([[3, 3,5], [3, 5, 9],[5,9,17]])
b = np.array([[10], [16],[30]])
x_0 = np.array([[0], [0],[0]])
x_list.append(x_0)
r_0 = b - np.dot(A, x_0)
# print(r_0)
r_list.append(r_0)
a_0 = np.vdot(r_0, r_0) / (np.vdot(r_0, np.dot(A, r_0)))  # 乘以用dot，(a,b)用vdot
x_1 = x_0 + np.dot(a_0, r_0)
x_list.append(x_1)

r = r_0
a = a_0
p = r_0
x = x_1
p_list.append(p)

for i in range(2):  # 总次数为n次，这里填n-1
    r = r - np.dot(a, np.dot(A, p))  # r1
    r_list.append(r)
    beita = np.vdot(r_list[-1], r_list[-1]) / np.vdot(r_list[-2], r_list[-2])  # beita 0
    p = r + np.dot(beita, p)  # p1
    p_list.append(p)
    a = np.vdot(r, r) / np.vdot(p, np.dot(A, p))  # a1
    x = x + np.dot(a, p)
    x_list.append(x)
pprint.pprint(x_list)
print()
pprint.pprint(p_list)
print()
pprint.pprint(r_list)

写的多了慢慢的思路清晰多了，继续加油！