基于声卡实现的音频存储示波器,可作为电磁学实验的测量仪表
Posted 天元浪子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于声卡实现的音频存储示波器,可作为电磁学实验的测量仪表相关的知识,希望对你有一定的参考价值。
文章目录
1 前言
十年前女儿读高中,电磁学是那个学期物理课的重点内容。女儿回家吐槽说课堂上的物理实验是纸上谈兵,老师只播放幻灯片和实验动画,并没有仪表可以直观地看到电磁实验中感应电流的变化。为了帮助女儿理解电磁感应,爷儿俩花了一星期时间,做了一个用声卡测量电磁实验中感应电流的软件,还有一套楞次定律的实验装置。
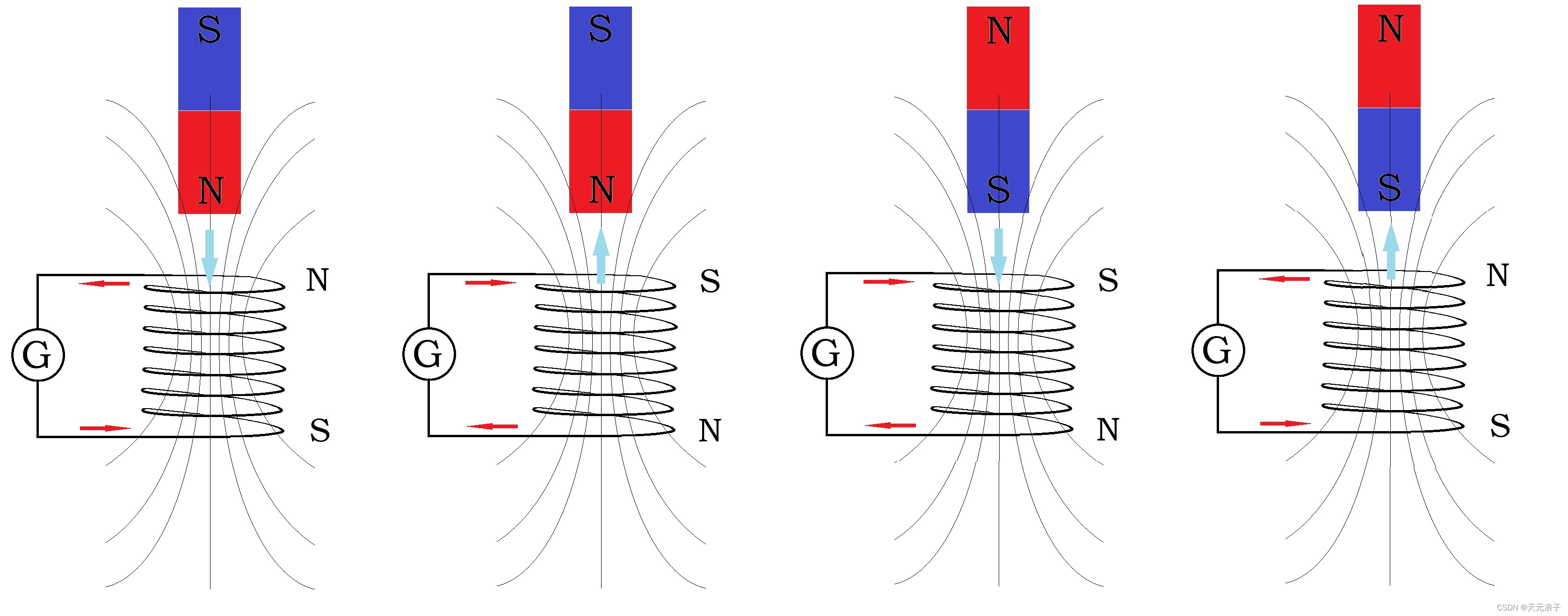
那时候,Python还是默默无闻的无名之辈,而我当时用的工具就是Python,GUI库用的是wxPython,数据采集和处理则是pyAudio模块和Numpy模块。时至今日,Python已成为最具影响力的开发工具,而pyAudio和Numpy依然非常活跃,wxPython也早已浴火重生,迎来了phoenix版。
最近有闲,整理了一下思路,依然使用pyAudio+Numpy+wxPython,重新设计了一个极具质感的音频存储示波器软件,希望能给正在学习电磁学的孩子和家长带来一些启发和帮助。倘若有机构或学校有兴趣在物理实验中使用这套工具软件,我愿意提供更多的协助。获取本项目完整的代码和资源文件请移步至GitHub。
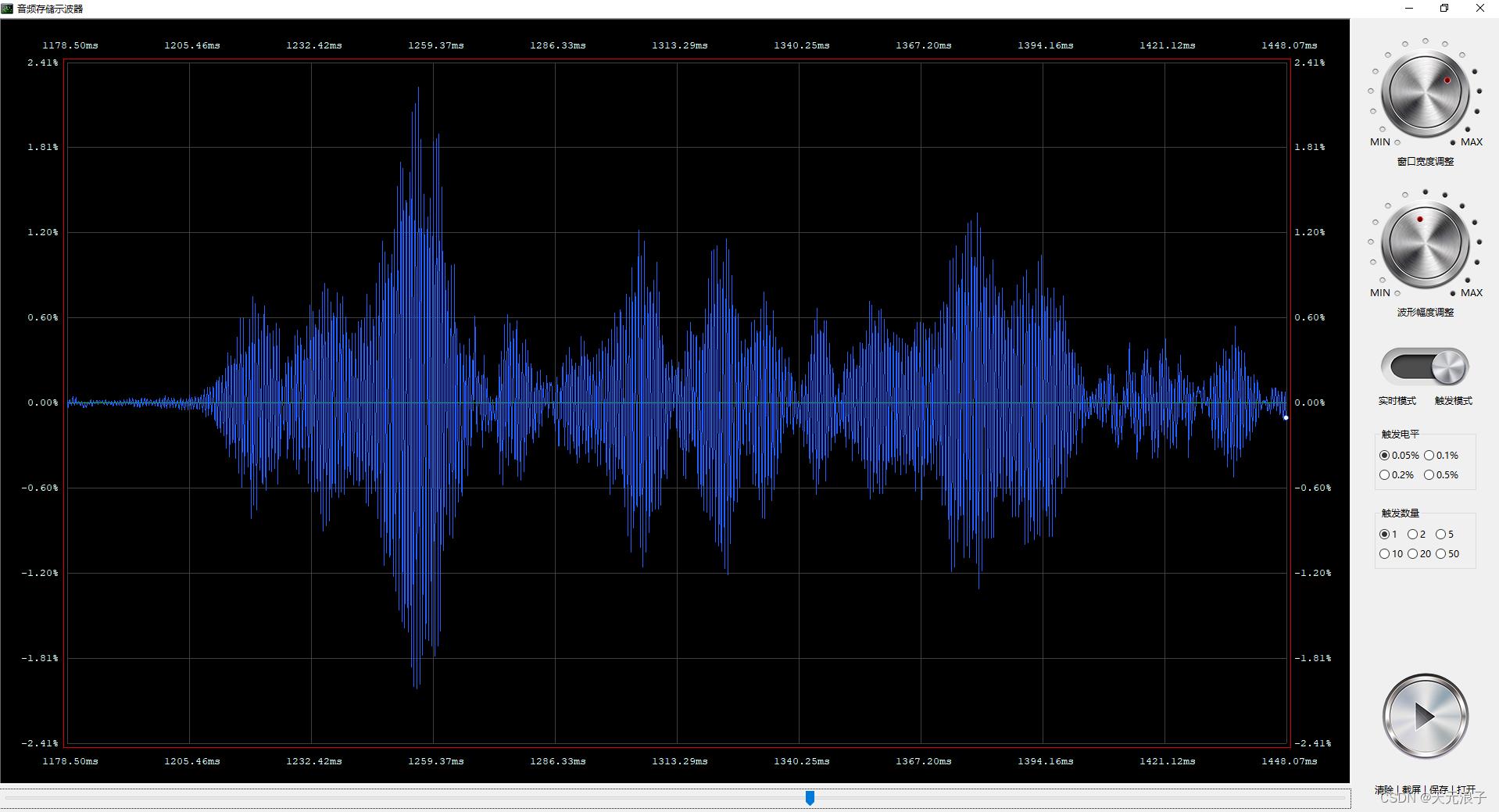
2 原理和架构
2.1 采样定理
音频信号属于模拟信号,经过声卡的信号采集和处理后成为计算机能够处理的数字化信息。模拟信号的数字化以采样定理为理论基础。采样定理,又称香农采样定理或奈奎斯特采样定理,描述起来非常简单:采样频率大于或等于有效信号最高频率的两倍,采样值就可以包含原始信号的所有信息,被采样的信号就可以不失真地还原成原始信号。采样定理暗含了两个基本概念,即采样频率和量化精度。
2.1.1 采样频率
对于声卡而言,采样频率是指每秒钟从连续的音频信号中采集并组成离散信号的采样个数,以赫兹(Hz)为单位。采样频率越高,声卡输出的采样数据就越多,对信号波形的表示也越精确。声卡常用的采样频率为22050Hz和44100Hz,能够复现的最大频率是10KHz和20KHz,分别对应调频广播级别的音质和CD级别的音质。
2.1.2 量化精度
声卡采集到的每一个数据点都以整型数据保存,整型数据的位数就是量化精度。常用的量化精度有8位、16位和24位等多种形式。以16位量化精度为例,每个采样数据占两个字节,表示的信号强度在-32768~32767之间。
2.2 软件架构
假设音频示波器的采样频率为44100Hz,量化精度选择16位,声卡每秒钟将产生88.2KB的数据,这些数据需要实时地显示在音频示波器的屏幕上。这里,声卡作为数据的生产者,音频示波器的屏幕作为数据的消费者,各自独立地从事自己的工作,又同时保持着严格的时序关系。这就是典型的生产者-消费者模式,这个模式的核心就是数据队列。

3 部件设计和装配
3.1 采样器
pyAudio是Python麾下一款历史悠久性能卓越的音频处理模块,尤其擅长声音采集。Audiosampler是基于pyAudio模块自定义的音频采集器类,默认采样频率为44100Hz,实例化时需要提供一个队列作为参数。采样器实例工作时,数据块被连续不断地写入队列。每个数据块大小默认为1024个采样点。采样器支持两种工作模式:实时模式和触发。所谓实时模式,就是输出所有的采样数据块;所谓触发模式,就是一个数据块内信号幅度超过触发阈值的采样点数量超过触发数量时才会输出,否则就丢弃。完整的采样器代码如下。
sample.py
# -*- coding: utf-8 -*-
import pyaudio
import numpy as np
class AudioSampler:
"""音频采样器"""
def __init__(self, dq, rate=44100):
"""构造函数"""
self.dq = dq # 数据队列
self.rate = rate # 采样频率
self.chunk = 1024 # 数据块大小
self.mode = 1 # 模式开关:0 - 触发模式,1 - 实时模式
self.level = 16 # 触发模式下的触发阈值
self.over = 1 # 触发模式下的触发数量
self.running = False # 采样器工作状态
def set_args(self, **kwds):
"""设置参数"""
if 'mode' in kwds:
self.mode = kwds['mode']
if 'level' in kwds:
self.level = kwds['level']
if 'over' in kwds:
self.over = kwds['over']
def start(self):
"""音频采集"""
pa = pyaudio.PyAudio()
stream = pa.open(
format = pyaudio.paInt16, # 量化精度(16位,动态范围:-32768~32767)
channels = 1, # 通道数
rate = self.rate, # 采样频率
frames_per_buffer = self.chunk, # pyAudio内部缓存的数据块大小
input = True
)
self.running = True
self.dq.queue.clear()
while self.running:
data = stream.read(self.chunk)
data = np.fromstring(data, dtype=np.int16)
if self.mode or np.sum([data > self.level, data < -self.level]) > self.over:
self.dq.put(data)
stream.close()
pa.terminate()
def stop(self):
"""停止采集"""
self.running = False
3.2 显示屏
Matplotlib是一个不错的绘图模块,但不适合绘制动态数据——尽管它有animation子模块,怎奈刷新速度跟不上每秒80KB的数据生产速度,只能另寻他途。这里,我用wx.DC配合Numpy的高效数据处理,以近乎“手工”的方式构造了一个示波器显示屏幕,可以轻松应对每秒80KB的数据的数据流量,毫无迟滞感。完整的示波器显示屏幕代码如下。
screen.py
# -*- coding: utf-8 -*-
import wx
import numpy as np
class Screen(wx.Panel):
"""示波器显示屏幕"""
def __init__(self, parent, rate=44100):
"""构造函数"""
wx.Panel.__init__(self, parent, -1, style=wx.SUNKEN_BORDER)
self.SetBackgroundColour(wx.Colour(0, 0, 0))
self.SetDoubleBuffered(True)
self.parent = parent # 父级控件
self.rate = rate # 采样频率
self.scale = 1024 # 信号幅度基准
self.tw = 32 # 以ms为单位的时间窗口宽度
self.pos = 0 # 时间窗口左侧在数据流上的位置
self.k = int(self.tw*self.rate/1000) # 时间窗口覆盖的数据点数
self.leftdown = False # 鼠标左键按下
self.mpos = wx._core.Point() # 鼠标位置
self.data = np.array([], dtype=np.int16) # 音频数据
self.scrsize = self.GetSize() # 示波器屏幕宽度和高度
self.args = self._update() # 绘图参数
self.font = wx.Font(10, wx.FONTFAMILY_DEFAULT, wx.FONTSTYLE_NORMAL, wx.FONTWEIGHT_NORMAL, False, 'Courier New')
self.Bind(wx.EVT_SIZE, self.on_size)
self.Bind(wx.EVT_PAINT, self.on_paint)
self.Bind(wx.EVT_MOUSEWHEEL, self.on_wheel)
self.Bind(wx.EVT_LEFT_DOWN, self.on_left_down)
self.Bind(wx.EVT_LEFT_UP, self.on_left_up)
self.Bind(wx.EVT_MOTION, self.on_mouse_motion)
def _update(self):
"""更新绘图参数"""
u_padding, v_padding, gap = 80, 50, 5 # 示波器屏幕左右留白、上下留白、边框间隙
args =
'b_left': u_padding, # 示波器边框左侧坐标
'b_top': v_padding, # 示波器边框顶部坐标
'b_right': self.scrsize[0] - u_padding, # 示波器边框右侧坐标
'b_bottom': self.scrsize[1] - v_padding, # 示波器边框底部坐标
'w': self.scrsize[0] - 2*(u_padding+gap), # 示波器有效区域宽度
'h': self.scrsize[1] - 2*(v_padding+gap), # 示波器有效区域高度
'mid': self.scrsize[1]/2, # 水平中心线高度坐标
'up': v_padding + gap, # 示波器有效区域顶部坐标
'down': self.scrsize[1] - v_padding - gap, # 示波器有效区域底部坐标
'left': u_padding + gap, # 示波器有效区域左侧坐标
'right': self.scrsize[0] - u_padding - gap # 示波器有效区域右侧坐标
x = np.linspace(args['left'], args['right'], self.k)
y = args['mid'] + (args['h']/2)*self.data[self.pos:self.pos+self.k]/self.scale
skip = max(self.k//args['w'], 1)
if x.shape[0] > y.shape[0]:
x = x[:y.shape[0]]
if skip > 1:
y = y[::skip]
x = x[::skip]
if y.shape[0] == 0:
y = np.array([args['mid']])
x = np.array([u_padding + gap])
else:
y = np.where(y < args['up'], args['up'], y)
y = np.where(y > args['down'], args['down'], y)
args.update('points':np.stack((x, y), axis=1), 'gu':args['w']/10, 'gv':args['h']/8)
return args
def _check_pos(self):
"""时间窗口位置校正"""
if self.pos < 0 or self.data.data.shape[0] <= self.k:
self.pos = 0
self.parent.slider.SetValue(0)
elif self.pos > self.data.data.shape[0] - self.k:
self.pos = self.data.data.shape[0] - self.k
self.parent.slider.SetValue(1000)
else:
self.parent.slider.SetValue(int(1000*self.pos/(self.data.data.shape[0] - self.k)))
def on_wheel(self, evt):
"""响应鼠标滚轮调整波形幅度"""
self.scale = self.scale*0.8 if evt.WheelRotation > 0 else self.scale*1.2
if self.scale < 32:
self.scale = 32
if self.scale > 32768:
self.scale = 32768
self.parent.vknob.SetValue(10 * (np.log2(self.scale)-5))
self.args = self._update()
self.Refresh()
def on_left_down(self, evt):
"""响应鼠标左键按下事件"""
self.leftdown = True
self.mpos = evt.GetPosition()
def on_left_up(self, evt):
"""响应鼠标左键弹起事件"""
self.leftdown = False
def on_mouse_motion(self, evt):
"""响应鼠标移动事件"""
if evt.Dragging() and self.leftdown:
pos = evt.GetPosition()
dx, dy = pos - self.mpos
self.mpos = pos
self.pos -= int(self.k * dx / self.scrsize[0])
self._check_pos()
self.args = self._update()
self.Refresh()
def on_size(self, evt):
"""响应窗口大小变化"""
self.scrsize = self.GetSize()
self.args = self._update()
self.Refresh()
def on_paint(self, evt):
"""响应重绘事件"""
dc = wx.PaintDC(self)
self.plot(dc)
def set_amplitude(self, value):
"""设置幅度缩放比例"""
self.scale = pow(2, 5 + value/10)
self.args = self._update()
self.Refresh()
def set_time_width(self, value):
"""设置时间窗口宽度"""
center = self.pos + self.k//2
self.tw = 0.1 * pow(1.1220184543019633, value)
self.k = int(self.tw*self.rate/1000)
self.pos = center - self.k//2
self._check_pos()
self.args = self._update()
self.Refresh()
def append_data(self, data):
"""追加数据"""
self.data = np.hstack((self.data, data))
self.pos = max(0, self.data.data.shape[0] - self.k)
self.args = self._update()
self.Refresh()
def set_pos(self, pos):
"""设置时间窗口位置"""
length = self.data.shape[0] - self.k
self.pos = int(length*pos/1000) if length > 0 else 0
self.args = self._update()
self.Refresh()
if self.pos == 0:
self.parent.slider.SetValue(0)
def clear(self):
"""清除数据"""
self.data = np.array([], dtype=np.int16)
self.pos = 0
self.args = self._update()
self.Refresh()
def plot(self, dc):
"""绘制屏幕"""
# 绘制中心水平线
dc.SetPen(wx.Pen(wx.Colour(0,224,0), 1))
dc.DrawLine(self.args['left'], self.args['mid'], self.args['right'], self.args['mid'])
# 绘制网格
dc.SetPen(wx.Pen(wx.Colour(64,64,64), 1))
dc.DrawLineList([(self.args['left']+i*self.args['gu'], self.args['up'], self.args['left']+i*self.args['gu'], self.args['down']) for i in range(0,11)])
dc.DrawLineList([(self.args['left'], self.args['up']+i*self.args['gv'], self.args['right'], self.args['up']+i*self.args['gv']) for i in [0,1,2,3,5,6,7,8]])
# 绘制数据
dc.SetPen(wx.Pen(wx.Colour(32,96,255), 1))
dc.DrawLines(self.args['points'])
dc.DrawCircle(self.args['points'][-1], 3)
# 绘制外边框
dc.SetPen(wx.Pen(wx.Colour(224,0,0),以上是关于基于声卡实现的音频存储示波器,可作为电磁学实验的测量仪表的主要内容,如果未能解决你的问题,请参考以下文章
基于MATLAB的高阶(两个二阶级联构成的四阶以及更高阶)数字图形音频均衡器系数计算(可直接用于DSP实现)