基于MATLAB的高阶(两个二阶级联构成的四阶以及更高阶)数字图形音频均衡器系数计算(可直接用于DSP实现)
Posted C0mm_notes
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于MATLAB的高阶(两个二阶级联构成的四阶以及更高阶)数字图形音频均衡器系数计算(可直接用于DSP实现)相关的知识,希望对你有一定的参考价值。
引言

前不久,在数字信号处理中需要对音频信号进行滤波,涉及图形均衡器、参数均衡器的设计,下面这个链接给出了一个图形音频均衡器的例子:
https://arm-software.github.io/CMSIS_5/DSP/html/group__GEQ5Band.html

这个示例演示如何使用 Biquad 级联函数构建 5 波段图形均衡器,每个波段均采用四阶的Biquad滤波器,每个滤波器由两个二阶的滤波器级联而成,图形均衡器用于音频应用中以改变音频的音质。
每一滤波段为四阶,由两个Biquad级联而成。每个滤波器的额定增益为0分贝(线性单位为1.0),并在特定频率范围内提升或削减信号。这5个频段之间的边缘频率分别为100、500、2000和6000Hz。每个频段都有一个在 ± 9 \\pm 9
高阶累积量基于高阶累积量的信噪比盲估计法的matlab仿真
1.软件版本
matlab2013b
2.系统描述
所谓高阶统计量,通常是指信号的高阶矩,高阶累积量等信号统计信息的统称。在这些高阶统计量中,高阶累积量具有十分重要的重用,不同阶数的累积量可以反映出信号的不同特征,因此高阶累积量往往应用在信号分类,信号调制方式识别等领域。高阶累积量中的二阶累积量和四阶累积量可以有效抑制高斯白噪声的干扰,且对相位偏移具有一定的容错能力,其数学表达式为:

MPSK发送信号为相互独立的同分布序列,则:

由于噪声的四阶累积量恒为零,噪声与信号独立,因此可以接收信号的高阶累积量可以表示为:


3.部分源码
function [c21,c42]=func_csum(yy)
N = length(yy);
sum_C21=0;
sum_C42=0;
for i = 1:100
C20=mean(yy.^2);
C21=mean(abs(yy).^2);
C41=mean((yy.^3).*conj(yy))-3*C20*C21;
C42=mean(abs(yy).^4)-abs(C20)^2-2*C21^2;
sum_C21=sum_C21+C21;
sum_C42=sum_C42+C42;
end
c21=sum_C21/100;
c42=sum_C42/100;
clc;
clear;
close all;
warning off;
%MPSK调制
%参数说明
% y 输出序列
% x 输入序列
% fc 载波频率
% fs 采样频率
% rc 码元速率
% M 调制模式M=2,4,8
x = rand(1,200)>=0.5;
fc = 16e6;
fs = 4*fc;
rc = 2e6;
M = 4;
detafy = 0*pi/6;
[y0,y_test] = func_MPSKgen(x,fc,fs,rc,M,detafy);
%%
%通过信号子空间估计信噪比
%通过高阶累积量估计信噪比
SNR = [0:0.5:20];
R1 = zeros(size(SNR));
R2 = zeros(size(SNR));
for sj = 1:length(SNR)
sj
y = awgn(y0,SNR(sj),'measured');
[c21,c42] = func_csum(y);%高阶累积量
SNRset1 = sqrt(abs(c42)/2)/(c21-0.965*sqrt(abs(c42)))+4;
SNRset2 = func_snr_est(y);
R1(sj) = SNRset1;
R2(sj) = SNRset2;
end
figure;
subplot(121)
plot(SNR,SNR,'r');
hold on
plot(SNR,R1,'o');
grid on
xlabel('SNR');
ylabel('高阶累积量');
legend('标准SNR','估计SNR');
title('高阶累积量估计信噪比');
subplot(122)
plot(SNR,SNR,'r');
hold on
plot(SNR,R2,'o');
grid on
xlabel('SNR');
ylabel('高阶累积量');
legend('标准SNR','估计SNR');
title('信号子空间估计信噪比');
sqrt(sum((SNR-R1).^2)/length(R1))
sqrt(sum((SNR-R2).^2)/length(R2))
4.仿真结论


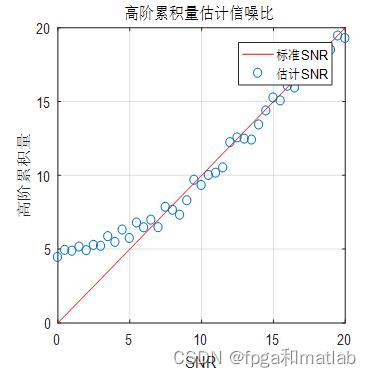
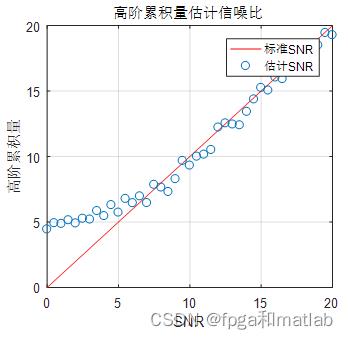
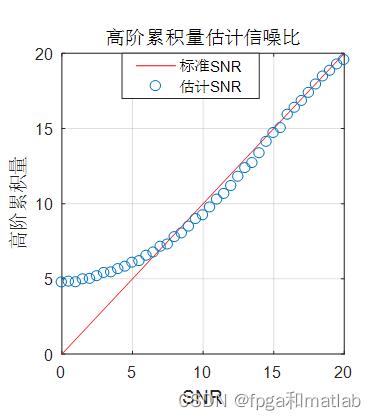
5.参考文献
[1]张安清,章新华.四阶累积量的递推估计及其应用.信号处理,2002,18(1):88~90.A01-151
 开发者涨薪指南
开发者涨薪指南
 48位大咖的思考法则、工作方式、逻辑体系
48位大咖的思考法则、工作方式、逻辑体系
以上是关于基于MATLAB的高阶(两个二阶级联构成的四阶以及更高阶)数字图形音频均衡器系数计算(可直接用于DSP实现)的主要内容,如果未能解决你的问题,请参考以下文章