算法2_非对称加密算法之ECDSA(椭圆曲线数字签名算法)

Posted 2023-04-01 Blockchain210

ECDSA(椭圆曲线数字签名算法)

AES(高级加密标准): =>对称加密

​ 对业务数据进行加密,防止他人可以看见

ECDSA(椭圆曲线数字签名算法):=>非对称加密算法(公钥和私钥)

​ 验证数据的真实性,防止业务数据被篡改

SHA(安全哈希算法)=>哈希算法

1. 作用:

因为ECDSA椭圆曲线数字签名算法获得公钥和私钥对是一一对应的,不存在"不同私钥但是公钥相同的情况"所有伪造ECDSA签名是根本不可能的

2. 解释ECDSA

ECDSA当中有两个词要注意:Curve(曲线)和Algorithm(算法)=>意味着ECDSA基本上是基于数学的

1. 基本原理:

假设给定一条曲线Curve、一串随机数Rand Num以及随机在曲线上取原点(Origin Point)

Private_Key=Rand_Num

Public_Key=Magic_Math(Curve,Rand_Num,Origin_Point)

=> 接下来就是要好好理解这个魔法数学Magic_Math =>(看完以下的就知道这个Magic_Math其实就是一个在已知椭圆曲线和参考点G的前提下对G进行以下运算)
$$Public\_Key=Rand\_Num\times Origin\_PointG(点的乘法)$$

3. 解释Magic_Math:

1. 前提

ECDSA只使用整数数学,没有浮点数

=>整数范围由签名当中所采用的位数决定的,更多的位数意味着更大的数字范围,更高的安全性能

​ why? 因为整数范围越大,则表示的位数越大那么破解ECDSA所需要猜测的数字范围也越大,那么破解所花费的时间越长,那么安全性就越高

=>mod 模运算:就是整数求除之后的余数

2. 椭圆曲线密码学

基于以下方程:
$$y^2=(x^3+a\ast x+b)modp$$

以上方程可以得知:
该方程所对应的曲线:对于任意的x坐标(只能取整数),你可以得到两个y的值,且曲线关于x轴对称。

p是一个素数,且确保所有得到的值在规定SHA的输出长度所能够表示的范围之内.

综上所述:经过取模运算之后结果只能在0-p-1之间,

总结:

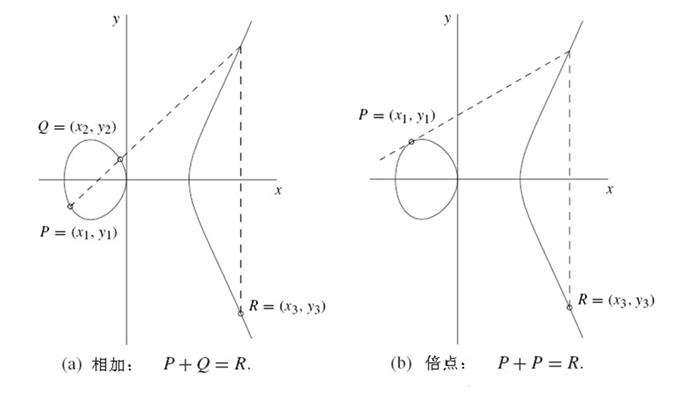
3. 椭圆曲线点加法的表示方法:

​ 注释:这是a=-4,b=0以后的椭圆曲线,P+Q点与R点对称
$$P=(x1,y1)P+Q=(X2,y2)=>X1=X2且Y1=-Y2$$
​ 所以对于椭圆曲线的点加法的定义是:在椭圆曲线上取两点P和Q进行加法运算结果为P+Q 等价于 P和Q的连接的延长线交于椭圆曲线R点,R点的对称点即P+Q

4. 椭圆曲线点乘法的表示方法:
$$k\ast P可以定义为P对自身进行k次相加获得点$$

5.椭圆曲线点乘法的单向陷门性
> 单向陷门函数的意思是:知道起点和终点不能求得乘数k,换句话说不知道怎么从起点开始做变换到达R点 正是这种单向陷门的性质是ECDSA的安全性的基础所在

4.ECDSA算法:

​ 首先你需要知道你的椭圆曲线参数的含义
$$椭圆曲线的数学表示:y^2=(x^3+a\times x+b)modp$$

$$其中abp是椭圆曲线中的参数,N是曲线面上符合该椭圆曲线数学表示的点个数,G是曲线上的任意一点作为起点$$

椭圆曲线的参数是由**NIST(National Institute of Standards and Technology)和SECG(Standards for Efficient Cryptography Group)** 这两个机构提供的已知高效和安全的标准化参数即提供了 a,b,p,G这四个参数

总结:综上所述
$$私钥dA是一串随机数公钥Qa是私钥dA\times G获得椭圆曲线终点即Qa=dA\times G$$

	Go标准库 crypto/ecdsa
	//私钥(或者说公私钥对)
	type PrivateKey struct 
		PublicKey  //所对应的公钥
		D *big.Int //私钥即随机数
	
	//公钥
	type PublicKey struct 
		//生成该公钥的椭圆曲线
		elliptic.Curve
		X, Y *big.Int //公钥的(X,Y)
	
	// GenerateKey generates a public and private key pair.
func GenerateKey(c elliptic.Curve, rand io.Reader) (*PrivateKey, error) 
	//k通过randFieldElement方法生成随机数作为私钥
	k, err := randFieldElement(c, rand)
	if err != nil 
		return nil, err
	
	
	priv := new(PrivateKey)
	//设置该公私钥对是基于的椭圆曲线
	priv.PublicKey.Curve = c
	//私钥
	priv.D = k
	//设置公钥
	priv.PublicKey.X, priv.PublicKey.Y = c.ScalarBaseMult(k.Bytes())
	return priv, nil

综上所述:
私钥是数,公钥是点坐标,PrivateKey既可以认为是私钥也可以认为是公私钥对

5.ECDSA算法进行数字签名过程:

​ 假设下面的哈希算法采用的是SHA1那么输出的长度为20字节,那么签名(R,S)中每个分量都是20字节

1. 问题:如何对一个文件或一个消息进行签名呢？

   过程:已知椭圆曲线参考点G、私钥dA以及产生一个随机数K

   $$1.P=k\times G(\times 是椭圆曲线上的点乘)$$

   $$2.P点的x坐标作为R(20字节)$$

   $$3.对消息Msg:z=SHA1(Msg)(z为20字节)$$

   $$4.S=k^{-1}(z+dA\times R)modp(k^{-1}是k的模的乘法逆元)$$

   $$最终的输出的是两元数组(R,S)$$

2. 问题:如何验证签名的合法性?

   过程:已知(R,S),公钥Qa,参考点G以及消息msg
   $$z=SHA(msg)$$

   $$P=S^{-1}\times z\times G+S^{-1}\times R\times Qa(第1,2个是椭圆曲线上的点乘算法)$$

   然后判断P的x坐标是否于R相等,如果相等则这个签名有效,否则是无效的

   有效的含义即这个Msg认为是真实且可信的

总结

1. 私钥是一个随机数，公钥是一个点.
2. 利用椭圆曲线上点乘是一个单向陷门函数特有的性质,作为ECDSA的安全性保证,使得生成公钥.
3. 参数a,b,p,G可以由NIST和SECG提供.
4. 了解数字签名和验证签名的过程,可以明白真正随机数的重要性.

参考文献

知乎之数海拾荒

孙荣燕,蔡昌曙,周洲,赵燕杰,杨金铭.国密SM2数字签名算法与ECDSA算法对比分析研究[J].网络安全技术与应用,2013(02):60-62.

椭圆曲线数字签名算法（ECDSA）

一． 椭圆曲线加密算法
简称ECC，是基于椭圆曲线数学理论实现的一种非对称加密算法。相比RSA，ECC优势是可以使用更短的密钥，来实现与RSA相当或更高的安全，RSA加密算法也是一种非对称加密算法，在公开密钥加密和电子商业中RSA被广泛使用。据研究，160位ECC加密安全性相当于1024位RSA加密，210位ECC加密安全性相当于2048位RSA加密（有待考证）
二． 什么是椭圆曲线
Wolfram MathWorld给出了个准确非凡的定义椭圆曲线。椭圆曲线可以暂时简单的理解为描述了特定点的集合的公式：

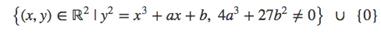
以下是a和b参数的变化对应的图形的示例：

b=1，a取值范围从2到-3

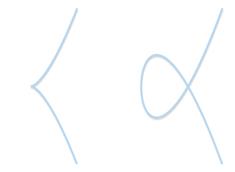
特殊曲线：左边参数是a=b=0，右边参数是a=-3，b=2.这两条都不是符合标准的曲线。
a和b的取值变化决定了曲线在坐标系上的不同形状。从图中可以看到，椭圆曲线是相对X轴对称。
另外定义一个无穷大的点（也可以成为理想点），以符号0，也就是零表示该点。
三． 阿贝尔群
椭圆曲线也可以有运算，像实数的加减乘除一样，这就需要使用到加群。19世纪挪威的尼尔斯·阿贝尔抽象出了加群（又叫阿贝尔群或交换群）。数学中的群是一个集合，我们为它定义了一个“加法”，并用符号+表示。假定群用 表示，则加法必须遵循以下四个特性：

封闭性：如果a和b都是 的成员，那么a+b也是 的成员；
结合律：(a + b) + c = a + (b + c);
单位元：a+0=0+a=a，0就是单位元；
逆元：对于任意值a必定存在b，使得a+b=0。

如果再增加一个条件，交换律：a + b = b + a，则称这个群为阿贝尔群，根据这个定义整数集是个阿贝尔群。

四． 椭圆的几何加法
因为椭圆曲线是阿贝尔群，所以公式P+Q+R=0 以及 P+Q=−R成立。在椭圆曲线上画出点P和点Q，连直线穿过P和Q，该直线会与椭圆曲线相较于第三个点，称之为R。根据R取得R的逆元-R，P+Q=-R。

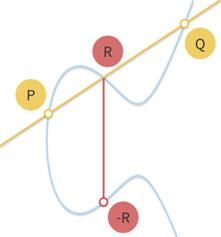
运用几何学的方法很容易得到我们要的结果，但是我们需要再对一些更精确的解释。特别是有一些问题需要考虑：
• 如果P=0或者Q=0(0是无穷远点)呢？无法画出该直线，因为无穷远点无法体现在直角坐标系里。但是既然已经定义了无穷远点0，那么对于任意给定的P或者Q，P+0=P以及0+Q=Q都是成立的。
• 如果P=-Q呢？这种情况下该直线是与X轴是垂直的，并且不会与椭圆曲线相交于第三个点。 根据公理，P就是Q的逆元，P+Q=P+(-P)=0。
• 如果P=Q呢？这种情况下，存在无数条线穿过这个点。这里要用到极限的思维。假设线上有另外一个点Q1，让Q1不断靠近P， 随着Q1不断靠近P，最终Q1无限靠近P，产生了一条直线与椭圆曲线相切。那么可以得到 P+P=-R, 在这里R就是该直线与椭圆曲线的另外一个交点。

• 如果P≠Q，但是不存在第三个交点R呢？这种情况和上一个情况很类似。实际上，这种情况下该直线跟椭圆曲线是相切的关系。

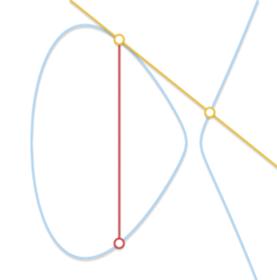
假设P就是相切的点。在上一个情况里，有该等式P+P=-Q。而在这里变成了P+Q=-P。另一方面，如果Q是相切的点，那么P+Q=-Q。
五. 代数上的加法
要计算点的加法的话，我们必须把前面的几何学的讨论转到代数上的讨论，考虑非0，非对称的点P(x1,y1)和Q(x2,y2)，R(x3,y3)为过P,Q与曲线相交点，则：
x3=k^2−x1−x2
y3=k(x1−x3)−y1
若P=Q,则k=(3x1^2+a)/2y1
若P≠Q,则k= (y2−y1)/ (x2−x1)

六． 标量乘法
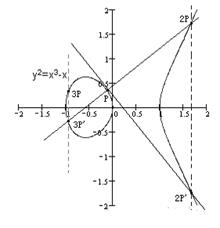
同点加法,若有k个相同的点P相加，记作kP 。 P+P=2P

P+P+P=2P+P=3P

七． 有限域椭圆曲线
椭圆曲线是连续的，并不适合用于加密；所以，我们必须把椭圆曲线变成离散的点，我们要把椭圆曲线定义在有限域上。
我们给出一个有限域Fp
1.Fp中有p（p为质数）个元素0,1,2,…, p-2,p-1
2.Fp的加法是a + b ≡ c ( m o d p )
3.Fp的乘法是a × b ≡ c ( m o d p )
4.Fp的除法是a ÷ b ≡ c ( m o d p ) ， 即 a × b ^− 1 ≡ c ( m o d p ) ， b^ − 1 也 是 一 个 0 到 p − 1 之 间 的 整 数 ， 但 满 足 b × b ^− 1 ≡ 1 ( m o d p )
5.Fp的单位元是1，零元是 0
6.Fp域内运算满足交换律、结合律、分配律
7.椭圆曲线Ep(a,b)，p为质数，x,y∈[0,p-1]

选择两个满足下列约束条件的小于p的非负整数a、b :

有限域椭圆曲线点的阶, 如果椭圆曲线上一点P，存在最小的正整数n使得数乘n P = O∞,则将n称为P的阶,若n不存在，则P是无限阶的.

八． 椭圆曲线加密
考虑K=kG，其中K、G为椭圆曲线Ep(a,b)上的点，n为G的阶（n G = O∞ ），k为小于n的整数。则给定k和G，根据加法法则，计算K很容易但反过来，给定K和G，求k就非常困难。因为实际使用中的ECC原则上把p取得相当大，n也相当大，要把n个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据 。

1.点G称为基点（base point）
2.k(k<n)为私有密钥（private key）
3.K为公开密钥（public key)

下面是利用椭圆曲线进行加密通信的过程（公钥加密私钥解密过程）：
1、用户A选定一条椭圆曲线Ep(a,b)，并取椭圆曲线上一点，作为基点G。
2、用户A选择一个私有密钥k，并生成公开密钥K=kG。
3、用户A将Ep(a,b)和点K，G传给用户B。
4、用户B接到信息后 ，将待传输的明文编码到Ep(a,b)上一点M（编码方法很多，这里不作讨论），并产生一个随机整数r（r<n）。
5、用户B计算点C 1 = M + r K和C 2 = r G。
6、用户B将C 1 、 C 2 传给用户A。
7、用户A接到信息后，计算C 1 − k C 2 ，结果就是点M。再对点M进行解码就可以得到明文。
因为C 1 − k C 2 = M + r K − k ( r G ) = M + r k G − k r G = M

九． 数字签名
数字签名是公钥密码学发展过程中最重要的概念之一，产生和使用数字签名过程的一般模型如图所示

十． 椭圆曲线数字签名算法（ECDSA）
ECDSA处理过程：
1.参与数字签名的所有通信方都使用相同的全局参数，用于定义椭圆曲线以及曲线上的基点
2.签名者首先生成一对公私钥。对于私钥，选择一个随机数或者伪随机数作为私钥，利用随机数和基点算出另一点，作为公钥
3.对消息计算Hash值，用私钥、全局参数和Hash值生成签名
4.验证者用签名者的公钥、全局参数等验证。
全局参数：

密钥生成：
每个签名者都要生成一对公私钥，假设是Bob

这里是定义在
上的椭圆曲线，椭圆曲线上的乘法运算就是多个点的累加运算，最后的结果还是椭圆曲线上的点，有了公钥之后，Bob对消息m生成320字节的数字签名：

第2步确保最后算出的公钥（椭圆曲线上的点）是落在曲线上。第5步，如果为O点也是不符合的，所以也要重新生成。
Alice在获得Bob的公钥和全局参数后，即可校验签名


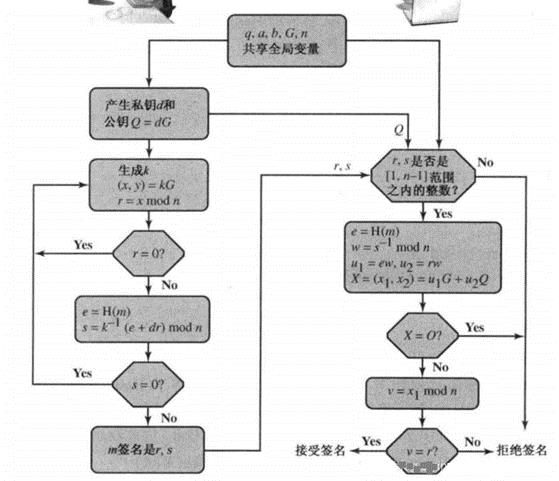
该过程有效性证明如下，如果Alice收到的消息确实是Bob签署的，那么
s = (e+dr)k^-1 mod n
于是 k= (e+dr)s^-1 mod n
= (e s^-1 + dr s^-1) mod n
= (we +wdr) mod n
=(u1 + u2d) mod n
现在考虑u1G + u2Q = u1G + u2dG = (u1 + u2d)G = KG
在验证过程的步骤6中，有v = x1 mod n , 这里解点 X =(x1,y1) = u1G + u2Q。因为
R = x mod n 且x 是解点kG的x 坐标，又因为 我们已知 u1G + u2Q = KG，所以可得到 v = r。