课程作业最优化理论与方法：第二次作业

Posted 2022-09-10 海轰Pro

目录

• 简介
• 3-16（C）
• 3-17
• 3-20
• 3-22 (C)
• 3-23 (B)
• 3-32
• 3-36 (e)
• 3-45
• 3-55
• 结语

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
本文仅记录自己感兴趣的内容

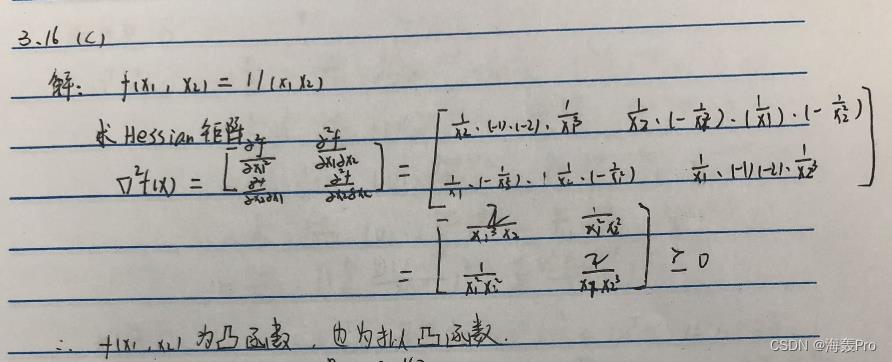
3-16（C）

函数$f(x_1,x_2)=1/(x_1{x}_2)$,定义域为$R_{++}^2$

3-17

设$p<1，p\ne 0$。证明定义域为$dom\int =R_{++}^n$的函数

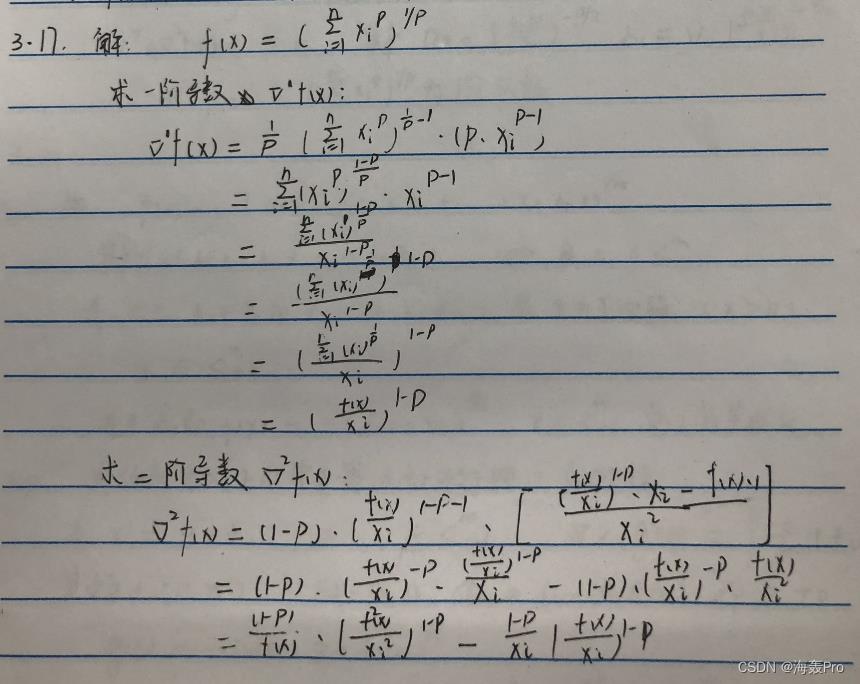
3-20

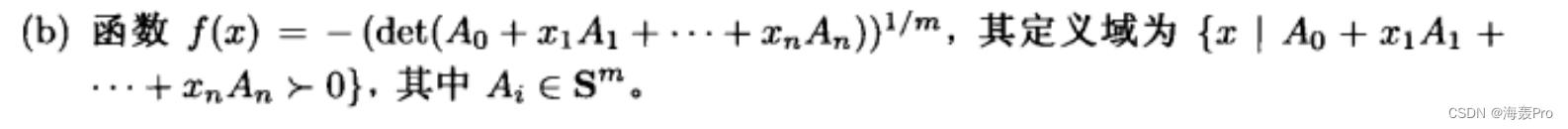
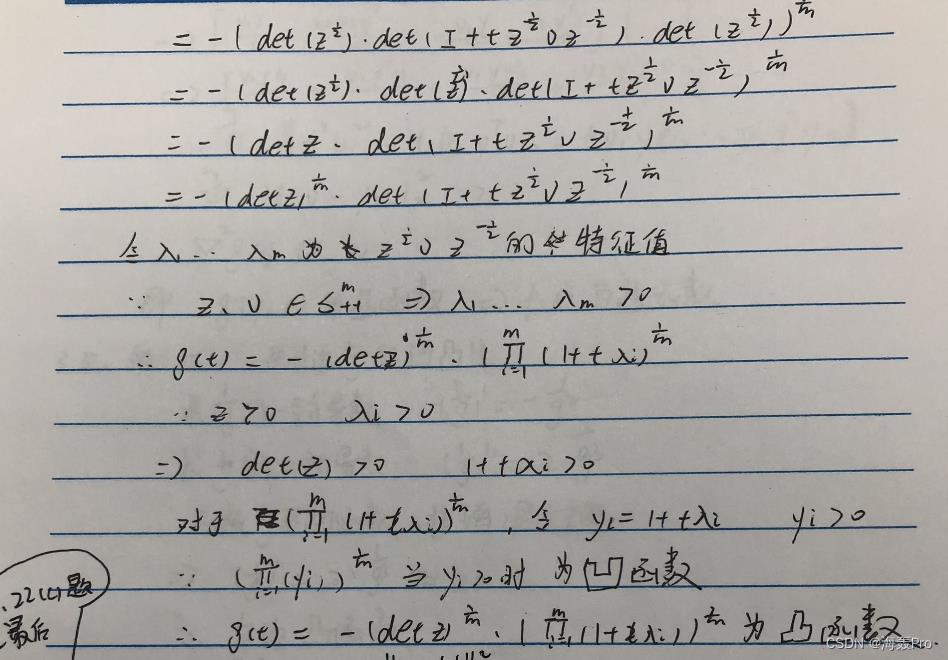
3-22 ©

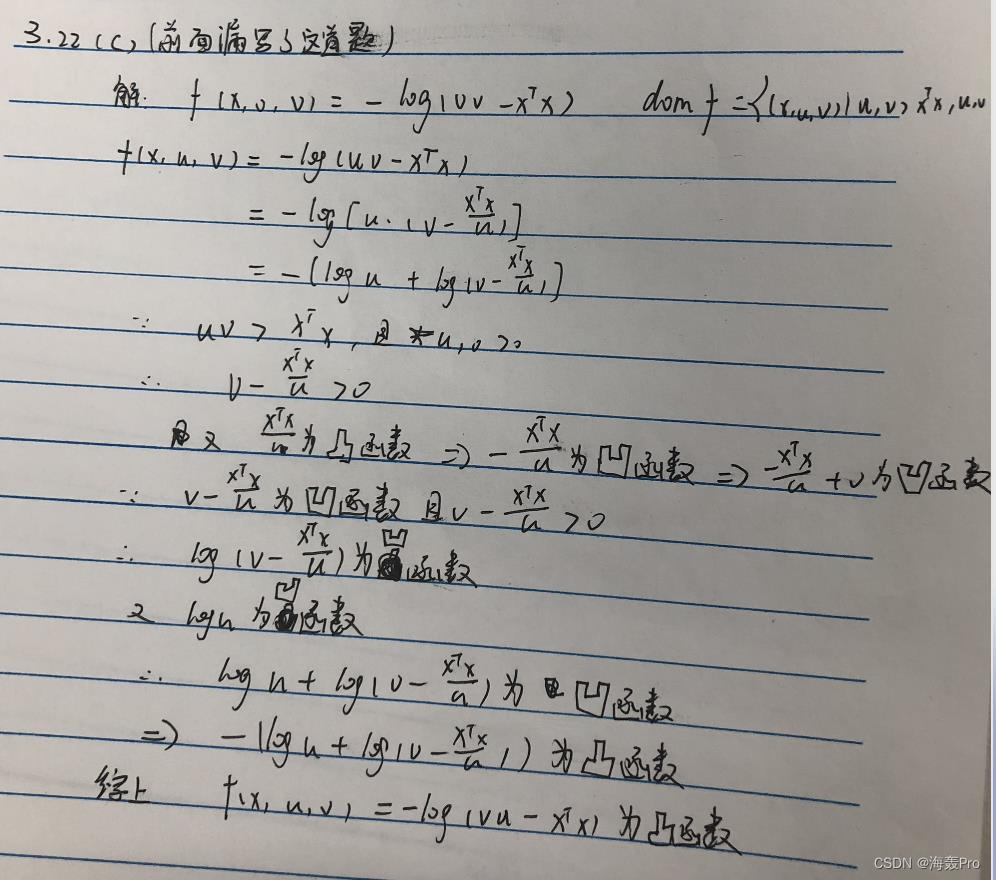
3-23 (B)

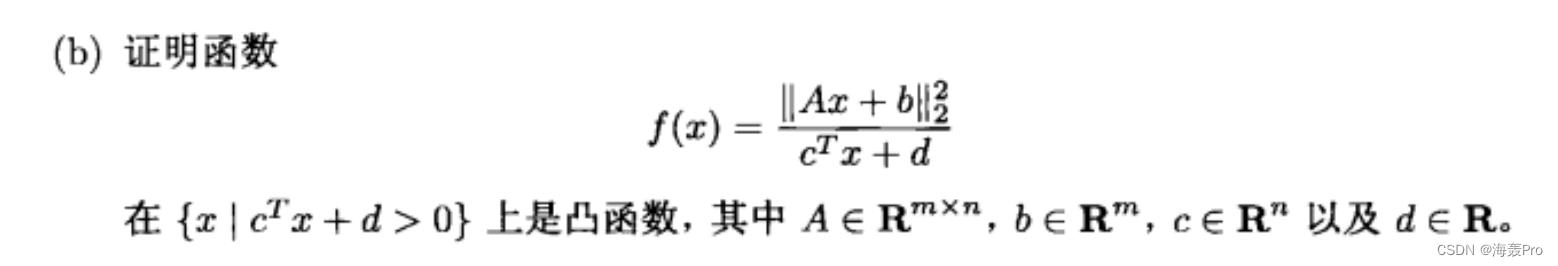
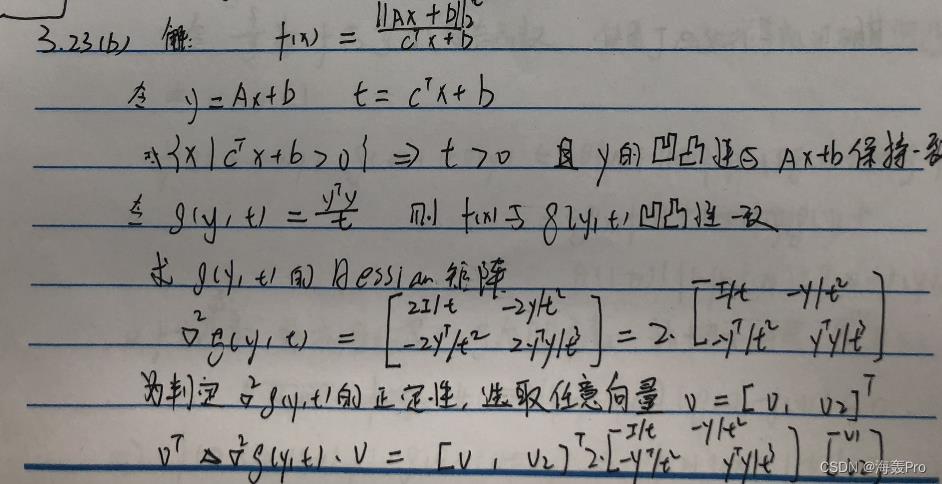
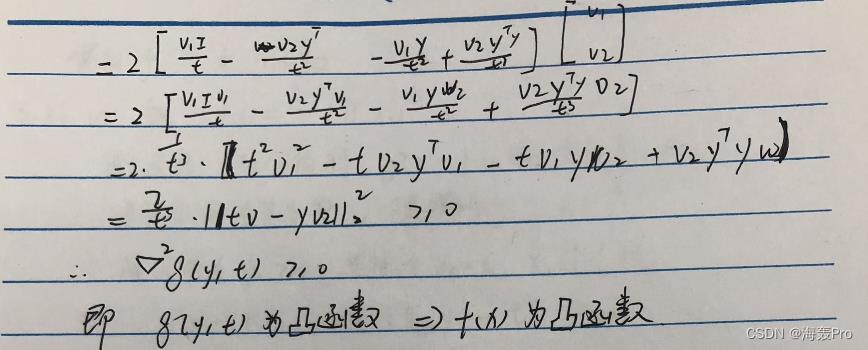
3-32

如果函数f是凸函数，非减且大于零，函数g是凹函数，非增，且大于零，那么函数 $f/g$是凸函数

3-36 (e)

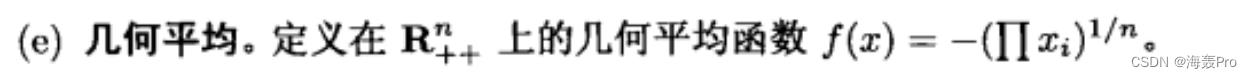
3-45

利用§3.4.3给出的判断拟凸性的一阶和二阶条件来证明函数$f(x)=-x_1{x}_2$的拟凸性，定 义域为$domf=R_{++}^2$

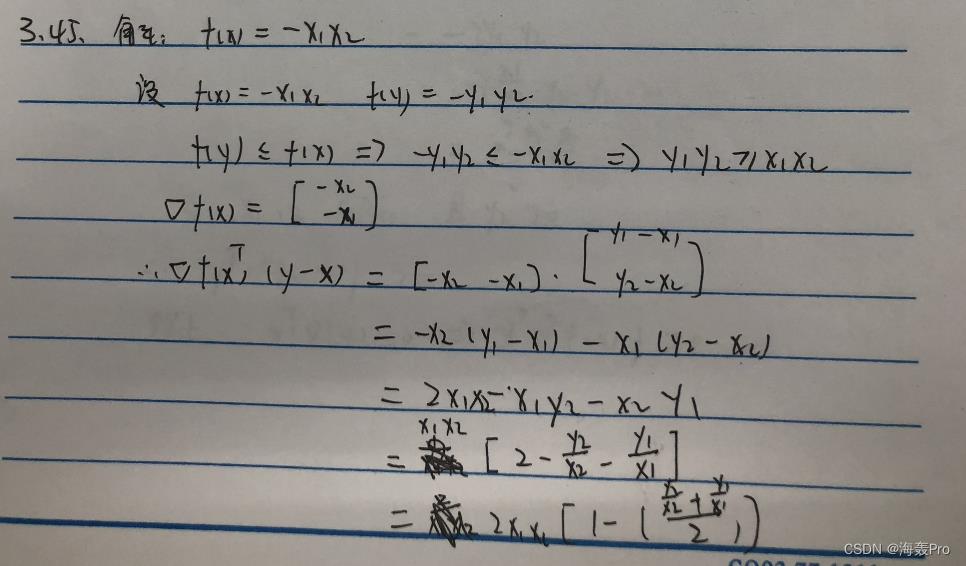
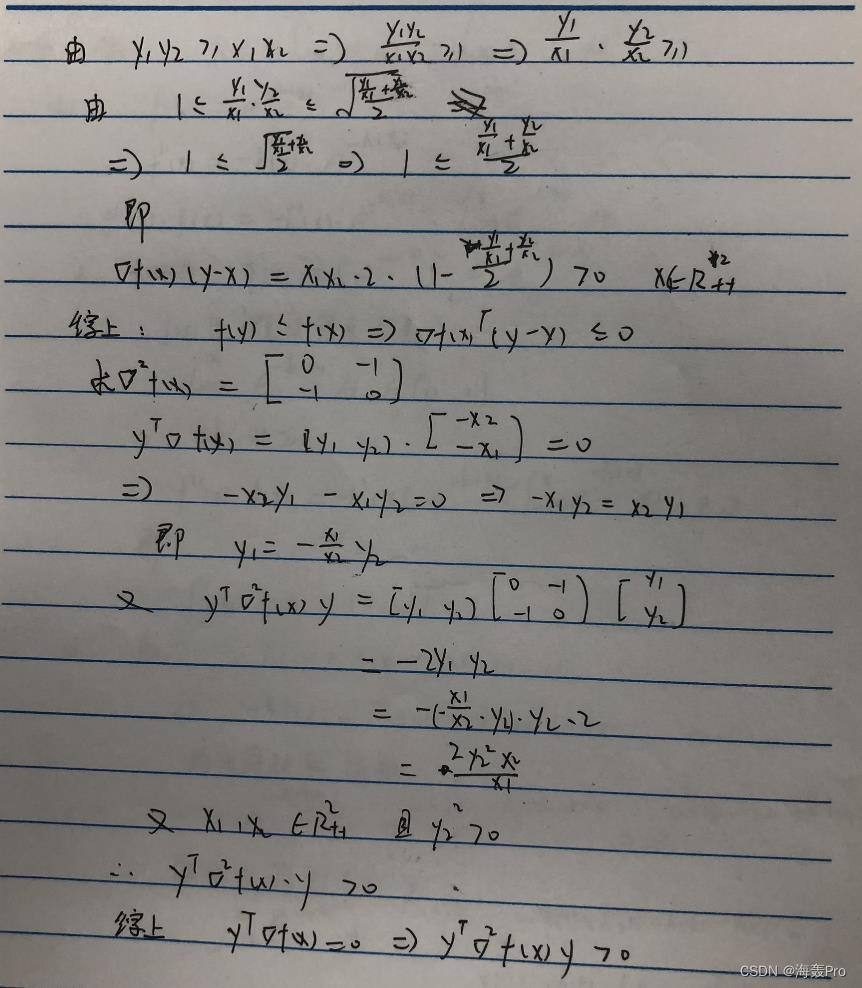
3-55

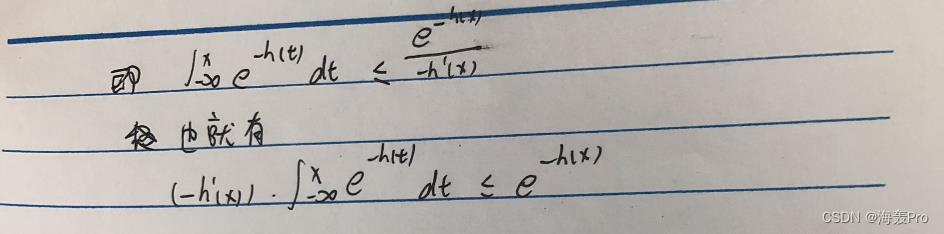
结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正