ZVS振荡电路工作原理分析

Posted 2022-09-01 卓晴

简 介： 本文基于 LTspice 仿真，分析了 ZVS 振荡器的工作原理以及相关的参数设计。

关键词： ZVS，LTspice，振荡器

 

§01 ZVS工作原理

---

一、背景介绍

  零电压开关（Zero Voltage Switch）振荡电路是功率开关管在导通和关断（模式切换时）两端电压为0（实际上应该是非常接近于0）的电路，这种特性使得电路功率损耗变小，所以被广泛 应用到大功率加热、高压电路中。比如在一些LLC 电源， 电磁炉驱动电路中。

  下面借助于 LTspice 仿真软件对 ZVS 的工作原理进行介绍。请大家注意，一开始在 LTspice搭建ZVS振荡器仿真 电路，电路并没有起振工作，经过调整仿真瞬态参数，设定仿真电路电源是从 0V 开始工作，这样电路便可以正常工作了。

▲ 图1.1.1 ZVS LTspice 仿真电路

1、需要回答的问题

  初次接触到 ZVS 的人对于这个电路形式可能会询问一下几个基本问题：

• 这个电路是如何振荡的？
• 电路器件参数是如何影响电路工作特性的？
• 电路中主要器件设计依据是什么？

二、电路振荡原理

1、多谐振荡器

  相比于常见到的 多谐振荡电路 ，ZVS电路结构也呈现鲜明的对称性，但其中元器件更多，而且还有 $LC$ 谐振回路，ZVS电路工作原理则显得更加的扑朔迷离。

  下面给出多谐振荡电路的基本电路原理图，如果你对于该电路工作原理比较熟悉，这也可以帮助你了解 ZVS 电路振荡原理。

▲ 图1.2.1 多谐振荡器原理图

  这类无稳态多谐振荡电路实际上是将两级反向放大电路串联成回路，信号经过回路形成正反馈从而使得电路中的三极管在两个状态（导通、截止）之间反转。下图给出了 LTspice 仿真后， Q1 的集电极和基极电压波形。

▲ 图1.2.2 多谐振荡器Q1的集电极和基极电压波形

2、二极管耦合电路

  观察 ZVS 电路，可以看到原来的两个耦合从 C1，C2 现在变成了二极管 D1，D2。下面给出了 ZVS 电路中最核心的六个器件组成的反向耦合电路。这个电路具有三个特殊的平衡状态。

• 平衡态1： M1截止，M2导通： 这是一个稳态。 M1截止，使得 D1不导通。 因此 R2 将电源施加在 M2 的栅极维持 M2 的导通； M2导通之后， D2 通过 M2 把 M1 的栅极接地，从而使得 M1继续截止。
• 平衡态2： M1导通，M2截止：这是一个稳态。分析的方法与上面稳态相同。
• 平衡态3： M1,M2处在放大状态 ： 这是一个不稳定的平衡态。

▲ 图1.2.3 ZVS电路中的核心器件

  在 LTspice 中，通过仿真可以计算出 M1，M2放大状态时， M1，M2 对应的漏极和栅极电压。下图给出了 M1 的栅极电压（Vn002）以及漏极（Vn004）。 电源通过 R1，R2 给 M1、M2 的栅极提供偏置电压，这个电压又通过 D1，D2 连接到 M2，M1的漏极。所以 M1，M2 的漏极比栅极电压低了一个二极管的导通电压（大约 0.7V）。

▲ 图1.2.4 LTspice 对M1,M2放大状态的仿真结果

  上面仿真验证了 M1、M2 都处在对称放大状态的存在，但这个状态属于不稳定状态， 一点点的扰动可能使得电路变换到平衡态 1 或者平衡态 2。 这是因为：

• 两个 MOS 管组成的放大电路，形成正反馈；
• 每一级 MOS 的放大电路的增益在平衡态时增益大于1；

3、MOS单管放大电路

  为了验证上面基本电路中 MOS 管处在放大状态下的增益大于1， 下面对 MOS 管电路放大特性进行仿真求解。

（1）MOS管单管跨导放大特性

  首先通过下图测试 MOS 管（IRF1310）的栅极电压与漏极电流之间的关系。

▲ 图1.2.5 测试 MOS 管的栅极电压 Vgs 与 漏极电流 Ids之间的关系

  下图给出了栅极电压与漏极电流之间的仿真结果。可以看到当输入电压超过 3.7V 之后， 漏极电流便开始快速上升。在不同的栅极电压下（或者说在不同的漏极电流 $I_{ds}=I_d$ 下） MOS 管的栅极电压与漏极电流之间的动态跨导 $D_{gd}$ 定义为：

$$D_{gd}\left(I_d\right)={\frac{d{I}_{ds}}{d{V}_{gs}}|}_{I_{ds}=I_d}$$

▲ 图1.2.6 MOS管栅极电压与漏极电流之间的关系

  利用仿真得到的数值 $V_{gs}\left[n\right],I_{ds}\left[n\right]$ ，通过各自的差分比值获得 MOS 栅极到漏极之间的跨导 $D_g\left[I_d\right]$ ，如下是计算出的曲线。 可以看到 MOS 的跨导与漏极电流大体上可以使用平方根函数进行建模，根据计算数据获建模参数为：

$$D_{gs}\left(I_g\right)=5.591\sqrt{I_g}$$

▲ 图1.2.7 MOS管跨导与漏极电流之间的关系以及平方根建模数据

（2）MOS单管放大器

  下面使用单个 MOS 管搭建放大电路，电路的放大倍数等于： $G=D_{gs}\left(I_d\right)\cdot R_1$ 。其中 $I_d$ 是电路静态漏极电流工作点。通过仿真可以求出 $I_d=24.6mA$ 。根据前面求出的跨导模型，可以计算出 $D_{gs}\left(0.0246\right)=5.56\sqrt{0.0246}=0.872$ ，因此，可以计算出电路放大倍数约为： $G=0.872\times 470=410$ 。

▲ 图1.2.8 单个MOS管放大电路

  下面是在电路输入施加 峰峰值为0.01V的信号时，电路输出峰值为1V的交流信号。因此电路实际放大倍数为 100 左右。

▲ 单个MOS管输入输出电压信号

  通过上述仿真计算，验证了 MOS 管处在放大状态增益远远大于 1。

4、ZVS振荡器

  由于二极管耦合电路具有两个稳态，所以该电路上电之后便停留在两个稳态之一，并不振荡。如果在两个 MOS 管的集电极增加一个电感之后，强制在两个 MOS 管的漏极之间建立一个直流通道，电路便不会在两个稳态之间持续停留了，会发生什么呢？下面看看仿真后的结果。

▲ 图1.2.10 在两个MOS管的漏极之间增加一个电感

  此时二极管耦合电路开始震荡，也就是在两个稳态之间来回切换。在上面电路图参数下，振荡频率为 213KHz，这应该是 L1 与 两个 MOS管杂散电容谐振的频率。

▲ 图1.2.11 M1，M2漏极电压信号

  如果在 L1 上并联一个电容 C1， 电路震荡频率由 L1、C1的谐振频率决定。

▲ 图1.2.12 在L1上并联谐振电容C1

  下图显示了并联谐振电容 C1 之后，电路上电后起振时两个 MOS 管漏极电压波形。震荡频率为 35.04kHz，这个频率与 C1、L1谐振频率相同。

▲ 图1.2.13 增加谐振电容电路起振后两个MOS管漏极电压波形

  通过以上分析可以看到 ZVS 基本电路起振原理比较简单，在二极管耦合电路的基础上，通过将 LC 谐振电路连接在两个 MOS 管的漏极，使得电路无法停留在两个稳态状态，只能够在两个稳态之间来回切换，切换的频率最终有 LC 谐振频率决定。

三、振荡电路的改进

1、电路缺点

  上面 ZVS 电路虽然能够振荡，但它存在一定的缺点。首先，电路振荡幅度不受控制。在电路每一次切换过程中， 在 C1 上的电压低于电源电压的器件， 电源总可以通过 R1，R2， D1，D2向 C1 充电，这个电能会叠加在 LC 谐振回路中。 当 C1 上的电压超过 12V 时， 截止的二极管和 MOS 管又阻止 LC中的能量消耗，这就会使的 LC 谐振电压越来越多。

  下图显示了电路在 0.1 秒钟之后 MOS 管漏极震荡电压就超过了 180V， 这个电压已经超过了 IRF1310 的 Vds 最高耐压了。

▲ 图1.3.1 MOS管电压波形

  电路的第二个缺点就是 LC 谐振回路带负载能力弱。 比如在 LC 谐振回路上并联一个负载电阻 R3（100欧姆）， 此时两个 MOS 管的漏极电压峰值降低到 3.3V。这主要是因为电源能量需要经过 R1、R2才能够补充到 LC 回路，所以损耗比较大。

▲ 图1.3.2 在LC谐振回路增加负载电阻R3之后的电路图

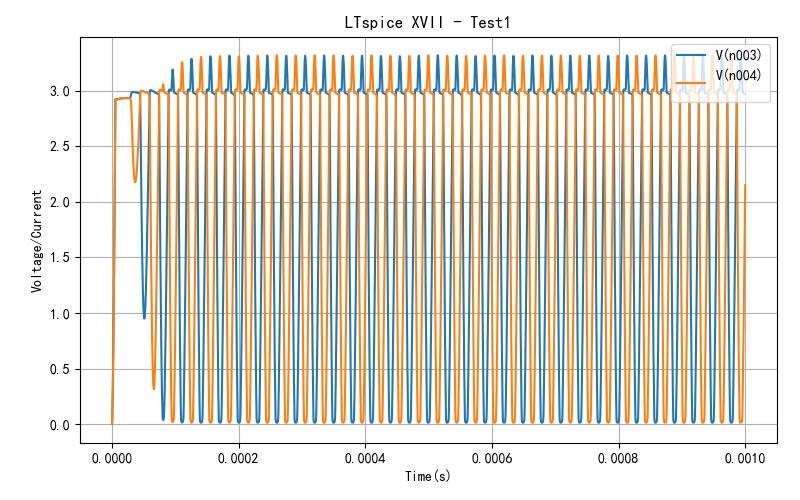
▲ 图1.3.3 增加负载之后MOS管漏极电压波形

2、电路改进

  为了消除上面的缺点，考虑将电源电压直接引入 LC 谐振回路。把原来的电感 L1 分成两个对称的电感 L1，L2，然后在使用一个扼流圈 L3 将 L1，L2 中点连接到电源 V1 上。这样电源直流电能便可以通过 电感 L3直接补充到谐振回路中了。

▲ 图1.3.4 通过扼流圈L3直接把电源引入LC谐振回路

  之所以使用扼流圈，也就是数值比较大的电感 L3 连接 LC 谐振回路到电源，是为了隔离 LC 谐振回路与电源之间的交流通道，即 LC 谐振回路的频率和波形不会因为接入电源而发生改变，因此要求 L3 的电感量比较大，需要比 L1、L2的电感量超出一个数量级以上。

  下面是电路中两个 MOS 管漏极电压以及 L1、L2 中点电压波形。

▲ 图1.3.5 两个MOS管漏极电压以及L1L2中点电压波形

  LC 谐振回路两端电压波形应该是正弦波，由于谐振回路两端被两个 MOS 管分别在两个半周期接地，所以在每个 MOS 管的漏极就出现了正弦波半波整流电压波形。 L1、L2中点的电压波形是两个 MOS 管漏极电压的平均值，所以它是正弦波的全波整流波形。

  施加在扼流电感 L3 两端的电压，一端是电源电压 V1， 一端是L1、L2中点电压。 当 L1、L2中点电压的平均值低于电源电压 V1 时， L3 中的流向谐振回路电流变化增加，持续向 LC 谐振回路增加能力。如果 L1、L2 中点电压平均值低于 电源电压 V1 时， L3 中的电流变化减少，甚至反向流向电源 V1。

  因此，在电路震荡平衡时， L1、L2 中点电压的平均值应该等于电源电压 V1。对于峰值为 E 的 全波整流信号，对应的平均值为 $2E/\pi$ ，所以有： $$\frac{2E}{\pi }=V_1$$

  MOS 管漏极电压峰值为 L1、L2 中点电压峰值的两倍，所以可以得到 MOS 管两端正弦半波整