ResNet-RS架构复现--CVPR2021
Posted 别团等shy哥发育
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ResNet-RS架构复现--CVPR2021相关的知识,希望对你有一定的参考价值。
ResNet-RS架构复现--CVPR2021
模型难复现不一定是作者的错,最新研究发现模型架构要背锅丨CVPR 2022
丰色 发自 凹非寺
量子位 | 公众号 QbitAI
在不同初始化条件下,同一神经网络经过两次训练可以得到相同的结果吗?
CVPR 2022的一篇研究通过将决策边界 (Decision Boundary)可视化的方法,给出了答案——
有的容易,有的很难。
例如,从下面这张图来看,研究人员就发现,ViT比ResNet要更难复现(两次训练过后,显然ViT决策边界的差异更大):

研究人员还发现,模型的可复现性和模型本身的宽度也有很大关联。
同样,他们利用这种方法,对2019年机器学习最重要的理论之一——双下降 (Double Descent)现象进行了可视化,最终也发现了一些很有意思的现象。

来看看他们具体是怎么做的。
更宽的CNN模型,可复现性更高
深度学习中的决策边界,可以用来最小化误差。
简单来说,分类器会通过决策边界,把线内线外的点归为不同类。
在这项研究中,作者从CIFAR-10训练集中选择了三幅随机图像,然后使用三次不同的随机初始化配置在7种不同架构上训练,绘制出各自的决策区域。
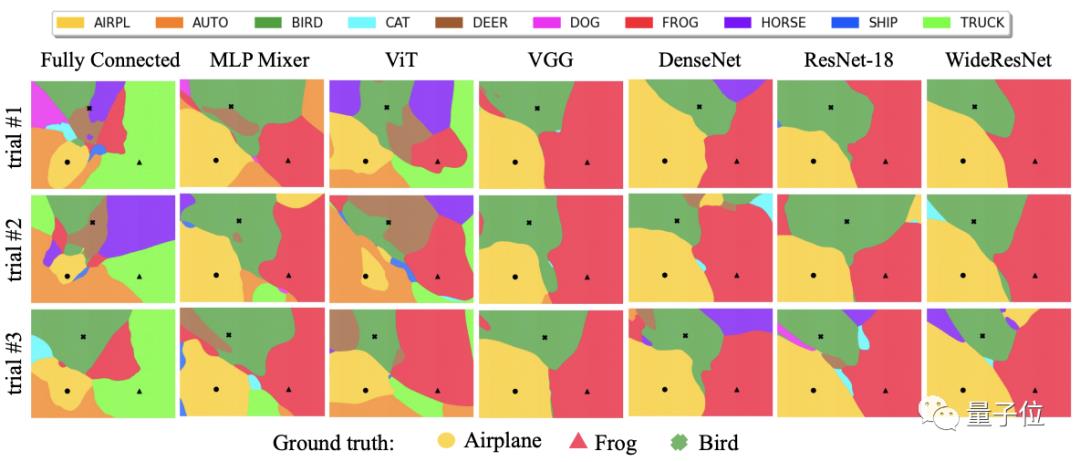
从中我们可以发现:
左边三个和右边四个差异很大,也就是说不同架构之间的相似性很低。
再进一步观察,左边的全连接网络、ViT和MLP Mixer之间的决策边界图又不太一样,而右边CNN模型的则很相似。
在CNN模型中,我们还可以观察到不同随机数种子之间明显的的重复性趋势,这说明不同初始化配置的模型可以产生一样的结果。
作者设计了一种更直观的度量方法来衡量各架构的可复现性得分,结果确实验证了我们的直观感受:

并发现更宽的CNN模型似乎在其决策区域具有更高的可复现性,比如WideRN30。
以及采用残差连接结构的CNN模型(ResNet和DenseNet )的可复现性得分比无此连接的模型要略高(VGG)。
此外,优化器的选择也会带来影响。
在下表中,我们可以看到SAM比标准优化器(如SGD和Adam)产生了更多可重复的决策边界。
不过对于MLP Mixer和ViT,SAM的使用不能总是保证模型达到最高的测试精度。

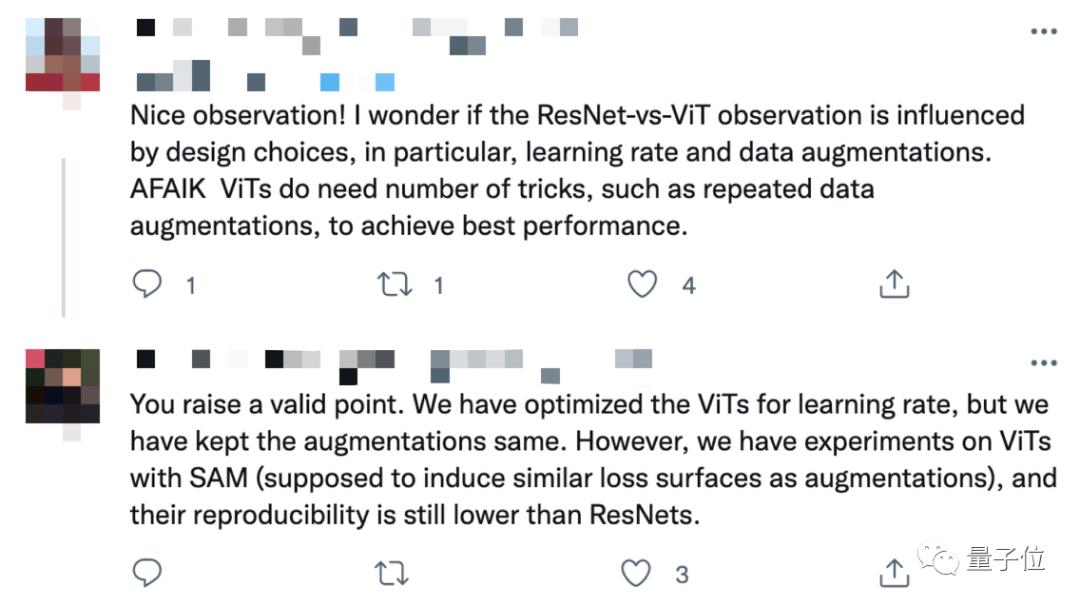
有网友表示好奇,如果通过改善模型本身的设计,能改变这种现象吗?
对此作者回应称,他们已经试着调整过ViT的学习率,但得到的结果仍然比ResNet差。
可视化ResNet-18的双下降现象
双下降(Double Descent)是一个有趣的概念,描述是测试/训练误差与模型大小的关系。
在此之前,大家普遍认为参数太少的模型泛化能力差——因为欠拟合;参数太多的模型泛化能力也差——因为过拟合。
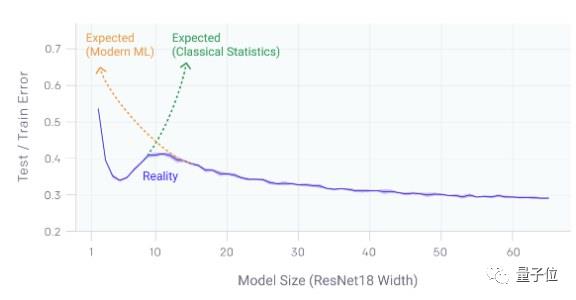
而它证明,两者的关系没有那么简单。具体来说:
误差会先随着模型的增大而减小,然后经过模型过拟合,误差又增大,但随着模型大小或训练时间的进一步增加,误差又会再次减小。
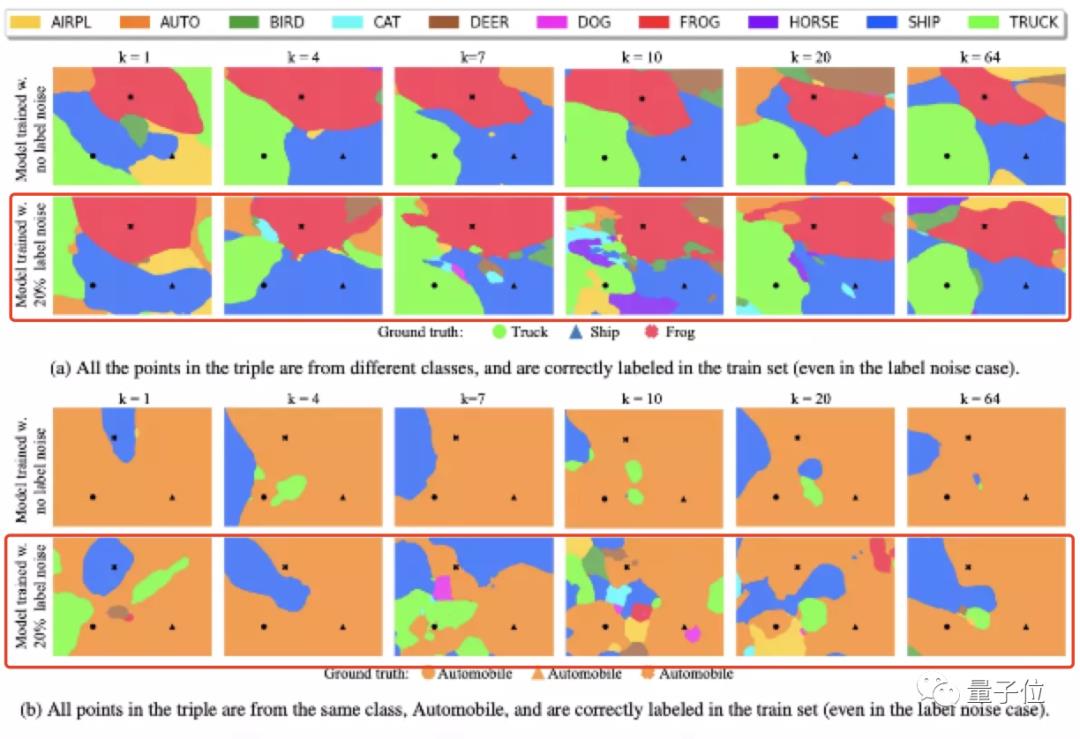
作者则继续使用决策边界方法,可视化了ResNet-18的双下降现象。
他们通过宽度参数(k:1-64)的改变来增加模型容量。
训练出的两组模型,其中一组使用无噪声标签(label noise)的训练集,另一组则带有20%的噪声标签。
最终,在第二组模型中观察到了明显的双下降现象。
对此作者表示:
线性模型预测的模型不稳定性也适用于神经网络,不过这种不稳定性表现为决策区域的大量碎片。
也就说,双下降现象是由噪声标签情况下决策区域的过度碎片引起的。
具体来说,当k接近/达到10 (也就是插值阈值)时,由于模型此时拟合了大部分训练数据,决策区域被分割成很多小块,变得“混乱和破碎”,并不具备可重复性;此时模型的分类功能存在明显的不稳定性。
而在模型宽度很窄(k=4)和很宽(k=64)时,决策区域碎片较少,有高水平的可重复性。
为了进一步证明该结果,作者又设计了一个碎片分数计算方法,最终再次验证上图的观察结果。
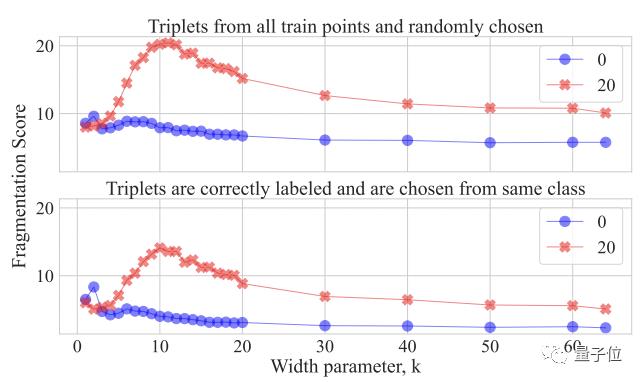
模型的可复现性得分如下:
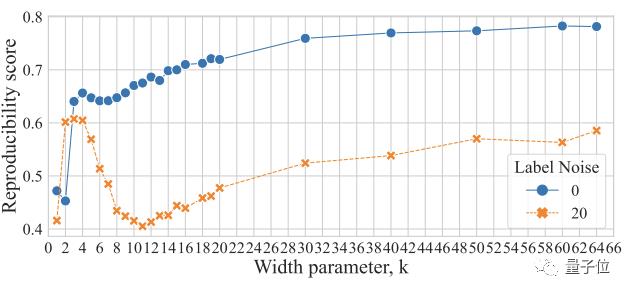
同样可以看到,在参数化不足和过参数化的情况下,整个训练过程的可复现性很高,但在插值阈值处会出现“故障”。
有趣的是,即使没有噪声标签,研究人员发现他们设计的量化方法也足够敏感,可以检测到可复现性的细微下降(上图蓝线部分)。
目前代码已经开源,要不要来试试你的模型是否容易复现?
论文地址:
https://arxiv.org/abs/2203.08124
GitHub链接:
https://github.com/somepago/dbVi
以上是关于ResNet-RS架构复现--CVPR2021的主要内容,如果未能解决你的问题,请参考以下文章
Log4j2注入漏洞(CVE-2021-44228)万字深度剖析—复现步骤(攻击方法)
繁凡的对抗攻击论文精读CVPR 2021 元学习训练模拟器进行超高效黑盒攻击(清华)
繁凡的对抗攻击论文精读CVPR 2021 元学习训练模拟器进行超高效黑盒攻击(清华)