Python机器学习基础知识和相关术语

Posted 2022-06-23 赵广陆

目录

• 1 函数定义
• • 1.1 线性函数
  • 1.2 二次函数或多次函数
  • 1.3 激活函数
  • 2.4 对数函数
• 2 机器学习的数据结构张量
• • 2.1 张量的概念
  • 2.2 标量——0D（阶）张量
  • 2.3 向量——1D（阶）张量
  • 2.4 矩阵——2D（阶）张量
  • 2.5 序列数据——3D（阶）张量
  • 2.6 图像数据——4D（阶）张量
  • 2.7 视频数据——5D（阶）张量

---

在学习之前先看一下：机器学习的数学基础

1 函数定义

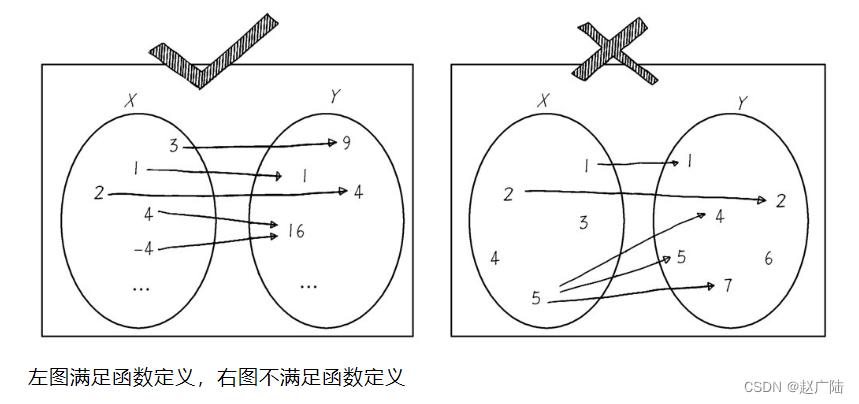
首先所有函数都要满足函数定义，函数的输出值是独一无二的。一个输入绝对不能够对应多个输出。比如，一张狗的图片，鉴定后贴标签时，认为既是哈士奇，又是德国牧羊犬。这种结果令人困惑，这样的函数我们也不接受。

1.1 线性函数

线性函数是线性回归模型的基础，也是很多其他机器学习模型中最基本的结构单元。线性函数是只拥有一个变量的一阶多项式函数，函数图像是一条直线。

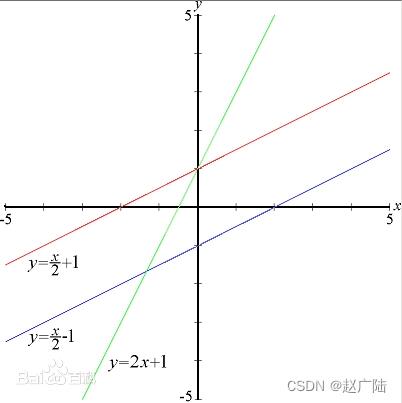
线性函数适合模拟简单的关系，比如，同一个小区房屋的面积和其售价之间可能会呈现线性的关系。

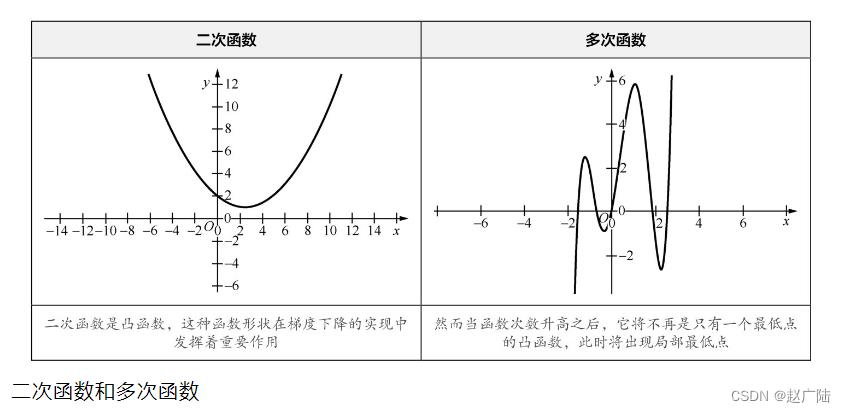
1.2 二次函数或多次函数

函数中自变量x中最大的指数被称为函数的次数，比如y=x^2就是二次函数。二次函数和多次函数的函数图像更加复杂，因而可以拟合出更为复杂的关系，如下图所示。

1.3 激活函数

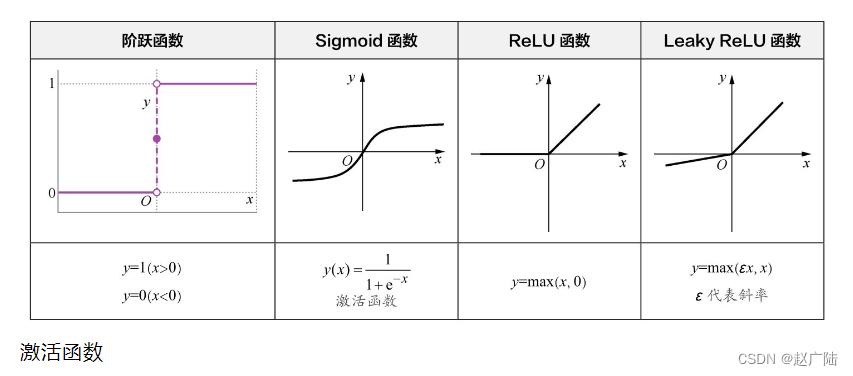
这组函数我们在数学课上也许没见过，但是它们都十分简单，它们的作用是在机器学习算法中实现非线性的、阶跃性质的变换。其中的Sigmoid函数在机器学习的逻辑回归模型中起着重要的作用。

2.4 对数函数

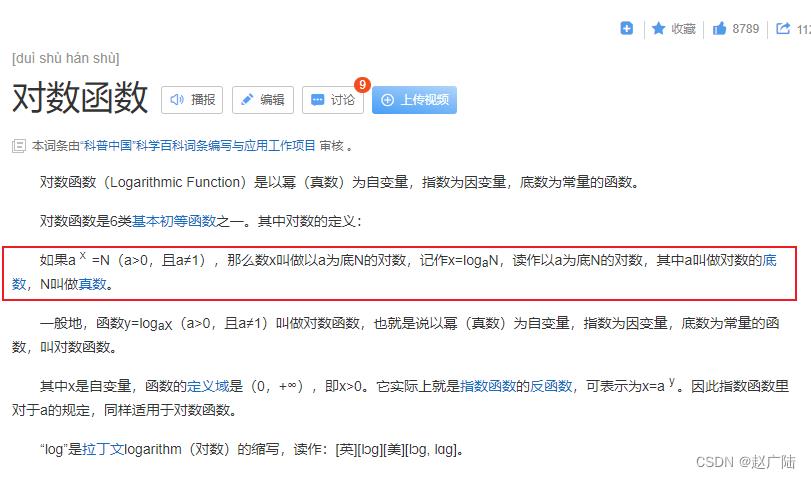
函数图像

注：如果不指定对数的底，则称x为自然对数，是以自然常数e为底数的对数。在逻辑回归算法中，我们会见到自然对数作为损失函数而出现。

2 机器学习的数据结构张量

2.1 张量的概念

张量是机器学习程序中的数字容器，本质上就是各种不同维度的数组，如下图所示。我们把张量的维度称为轴（axis）（就是数学中的x轴，y轴，……），轴的个数称为阶（rank）（也就是俗称的维度，但是为了把张量的维度和每个阶的具体维度区分开，这里统一把张量的维度称为张量的阶。NumPy中把它叫作数组的轶）。

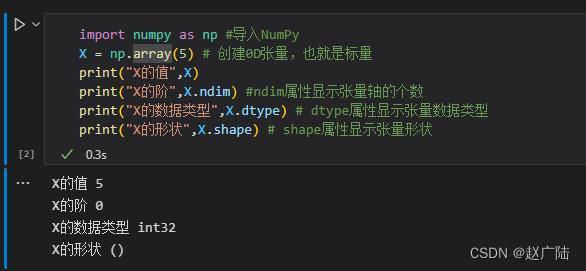
2.2 标量——0D（阶）张量

import numpy as np #导入Num Py库 
X = np.array(5) #创建0D张量, 也就是标量
print("X的值", X)
print("X的阶", X.ndim) #ndim属性显示标量的阶
print("X的数据类型", X.dtype) #dtype属性显示标量的数据类型
print("X的形状", X.shape) #shape属性显示标量的形状

运行结果：

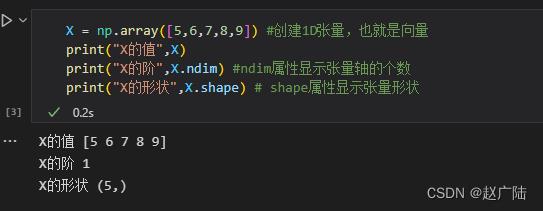
2.3 向量——1D（阶）张量

由一组数字组成的数组叫作向量（vector），也就是一阶张量，或称1D张量。一阶张量只有一个轴。

X = np.array([5,6,7,8,9]) #创建1D张量，也就是向量
print("X的值",X)
print("X的阶",X.ndim) #ndim属性显示张量轴的个数
print("X的形状",X.shape) # shape属性显示张量形状

运行结果：

2.4 矩阵——2D（阶）张量

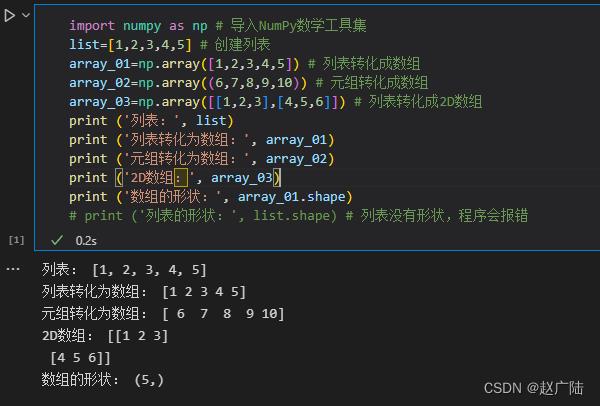
矩阵（matrix）是一组一组向量的集合。矩阵中的各元素横着、竖着、斜着都能构成不同的向量。而矩阵，也就是 2 阶张量，或称 2D 张量，其形状为（m，n）。比如，右图所示是一个形状为（4，3）的张量，也就是4 行 3 列的矩阵,一般就是表格数据长这个样子。

import numpy as np # 导入NumPy数学工具集
list=[1,2,3,4,5] # 创建列表
array_01=np.array([1,2,3,4,5]) # 列表转化成数组
array_02=np.array((6,7,8,9,10)) # 元组转化成数组
array_03=np.array([[1,2,3],[4,5,6]]) # 列表转化成2D数组
print ('列表：', list)
print ('列表转化为数组：', array_01)
print ('元组转化为数组：', array_02)
print ('2D数组：', array_03)
print ('数组的形状：', array_01.shape)
# print ('列表的形状：', list.shape) # 列表没有形状，程序会报错

运行结果：

2.5 序列数据——3D（阶）张量

# 创建3D张量
X = np.array([[[1, 22, 4, 78, 2],
[2, 59, 6, 56, 1],
[3, 31, 8, 54, 0]],
[[4, 56, 9, 34, 1],
[5, 78, 8, 35, 2],
[6, 34, 7, 36, 0]],
[[7, 45, 5, 34, 5],
[8, 53, 6, 35, 4],
[9, 81, 4, 36, 5]]])

运行结果：

举个现实的例子：

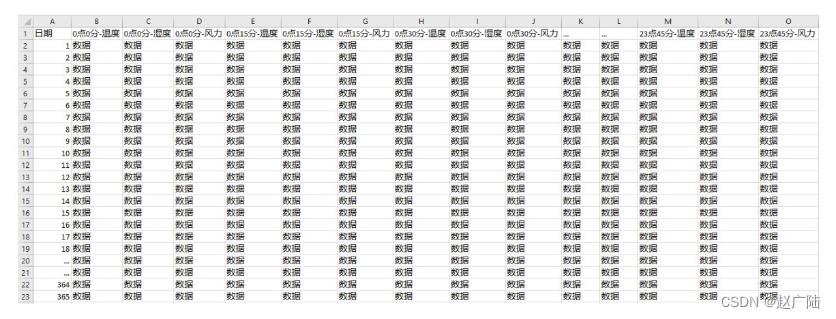
因为增加了时戳，所以表里面的行列结构显得更为复杂。读取入机器进行处理时，需要把行里面的时间步拆分出来。

第一个轴—样本轴，一年记录下来的数据共365个，也就是365维。
第二个轴—时间步轴，每天一共是24小时，每小时4个15分钟，共96维。
第三个轴—特征轴，一共是温度、湿度、风力3个维度。
因此，这个数据集读入机器之后的张量形状是（365，96，3）。

2.6 图像数据——4D（阶）张量

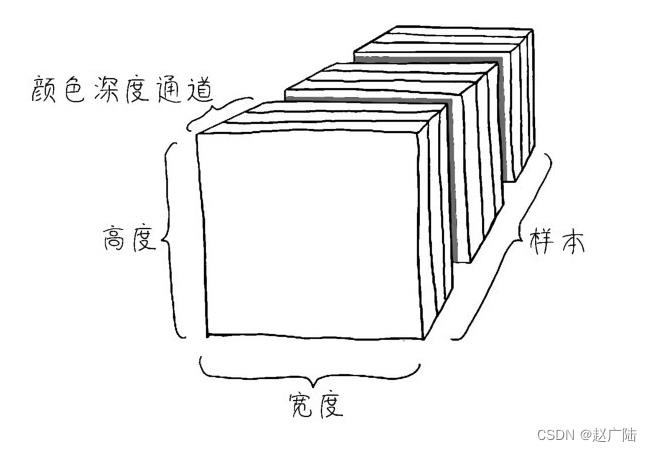
图像数据本身包含高度、宽度，再加上一个颜色深度通道。MNIST数据集中是灰度图像，只有一个颜色深度通道；而GRB格式的彩色图像，颜色深度通道的维度为3。

因此，对于图像数据集来说，长、宽、深再加上数据集大小这个维度，就形成了 4D 张量（如下图所示），其形状为（样本，图像高度，图像宽度，颜色深度），如MNIST特征数据集的形状为（60000，28，28，1）。

2.7 视频数据——5D（阶）张量

机器学习的初学者很少有机会见到比4D更高阶的张量。如果有，视频数据的结构是其中的一种。
视频可以看作是由一帧一帧的彩色图像组成的数据集。、

■每一帧都保存在一个形状为（高度，宽度，颜色深度） 的3D张量中。
■一系列帧则保存在一个形状为（帧，高度，宽度，颜色深度） 的4D张量中。
因此，视频数据集需要5D张量才放得下，其形状为（样本，帧，高度，宽度，颜色深度）。

可以想象，视频数据的数据量是非常大的（例如，一个10分钟的普通视频，每秒采样3～4帧，这个视频转换成机器能处理的张量后，可能包含上亿的数据量）。面对这种规模的数据，普通的机器学习模型会感到手足无措，只有深度学习模型才能够搞定。

开发者涨薪指南 48位大咖的思考法则、工作方式、逻辑体系