黄佳《零基础学机器学习》chap2笔记

Posted 2022-12-14 临风而眠

黄佳 《零基础学机器学习》 chap2笔记

第2课 数学和Python基础知识

文章目录

• 黄佳 《零基础学机器学习》 chap2笔记
• 第2课 数学和Python基础知识
• 2.1 函数描述了事物间的关系
• • 机器学习中常用的一些函数
• 2.2 捕捉函数的变化趋势
• 2.3 梯度下降
• 2.4 机器学习的数据结构--张量
• • 2.4.1 张量的轴、阶和形状
  • 2.4.2 标量--0D(阶)张量
  • 2.4.3 向量--1D(阶)张量
  • 2.4.4 矩阵--2D(阶)张量
  • 2.4.5 序列数据--3D(阶)张量
  • 2.4.6 图像数据--4D(阶)张量
  • 2.4.7 视频数据--5D(阶)张量
  • 2.4.8 数据的维度和空间的维度
• 2.5 Python的张量运算
• • 2.5.1 机器学习中张量的创建
  • 2.5.2 通过索引和切片访问张量中的数据
  • 2.5.3 张量的整体操作和逐元素运算
  • 2.5.4 张量的变形和转置
  • 2.5.5 Python中的广播
  • 2.5.6 向量和矩阵的点积运算
• 2.6 机器学习的几何意义
• • 2.6.1 机器学习的向量空间
  • 2.6.2 深度学习和数据流形
• 2.7 概率与统计研究了随机事件的规律
• • 2.7.1 什么是概率
  • 2.7.2 正态分布
  • 2.7.3 方差和标准差
• 2.8 本章小结
• 2.9 习题

2.1 函数描述了事物间的关系

• 这里讲的不错哈哈👇

  • 函数的输入和输出，很多情况下都是数字，但是也不完全如此。

  • 函数可以反映非数字之间的关系。

    • 比如，函数的输入可以是编号，输出可以是人名，关系就是“S11055607”→“黄先生”。在机器学习中，反映非数字之间的关系的函数就更常见了，比如，从狗的图片(输入）到狗的种类（输出)。

  • 有以下两点需要注意。

    • 输入集中的每一个元素X都要被“照顾”到(不过输出集并不一定需要完全覆盖。想象一下有一组狗的图片，全部鉴别完之后，发现其中缺少一个类型的狗，这是可能的)
    • 函数的输出值是独一无二的。一个输入绝对不能够对应多个输出。比如，一张狗的图片，鉴定后贴标签时，认为既是哈士奇，又是德国牧羊犬。这种结果令人困惑，这样的函数我们也不接受。

• 机器学习中的函数

  • 机器学习基本上等价于寻找函数的过程。机器学习的目的是进行预测、判断，实现某种功能。通过学习训练集中的数据，计算机得到一个从x到y的拟合结果，也就是函数。然后通过这个函数，计算机就能够从任意的x，推知任意的y。这里的自变量x，就是机器学习中数据集的特征，而特征的个数，通常会多于一个，记作x1，x2，…，xn,。如下图中的示例:机器学习通过电影的成本、演员等特征数据，推测这部电影可能收获的票房。

    

• 机器学习到的函数，实现了从特征到结果的一个特定推断。
  机器学习到的函数模型有时过于复杂，并不总是能通过集合、解析式或者图像描述出来。

  • 然而，不能直观描述，并不等于函数就不存在了，机器学习所得到的函数正是事物之间的关系的体现，并发挥着预测功能。
  • 换句话说，大数据时代的机器学习，不是注重特征到标签之间的因果逻辑，而是注重其间的相关关系。
  • 那么如何衡量通过机器学习所得到的函数是不是好的函数呢?
    • 在训练集和验证集上预测准确，而且能够泛化到测试集，就是好函数。
    • 对结果判断的准确性，是机器学习函数的衡量标准，在这个前提之下，我们把科学体系中原本的核心问题“为什么”，转移到了“是什么”这个更加实用的目标。

• 可以说，机器学习算法得到的函数，往往能看到数据背后隐藏着的、肉眼所不能发现的秘密。

机器学习中常用的一些函数

传统的机器学习算法包括线性回归、逻辑回归、决策树、朴素贝叶斯等，通过应用这些算法可以得到不同的函数。

而深度学习的函数具有复杂的神经网络拓扑结构，网络中的参数通过链式求导来求得，相当于一大堆线性函数的跨层堆叠。它们仿佛存在于一片混沌之中，虽然看不见摸不着，却真实地存在着。

无论是传统的机器学习，还是深度学习，所得到的函数模型都是对样本集中特征到标签的关系的总结，是其相关性的一种函数化的表达。

• 线性函数

  • 线性函数适合模拟简单的关系，比如，同一个小区房屋的面积和其售价之间可能会呈现线性的关系。

• 二次函数和多次函数

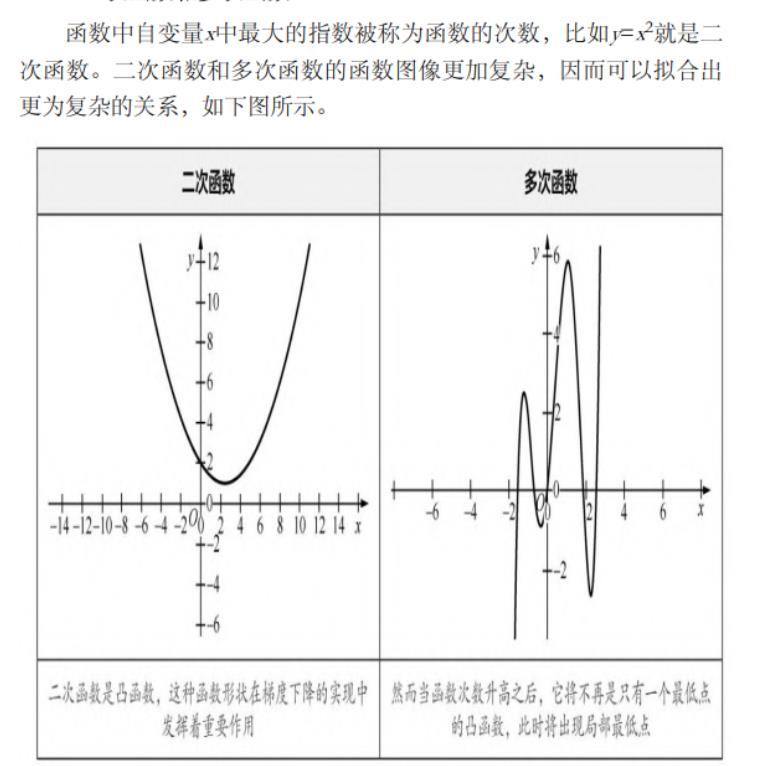
• 激活函数（activation function）

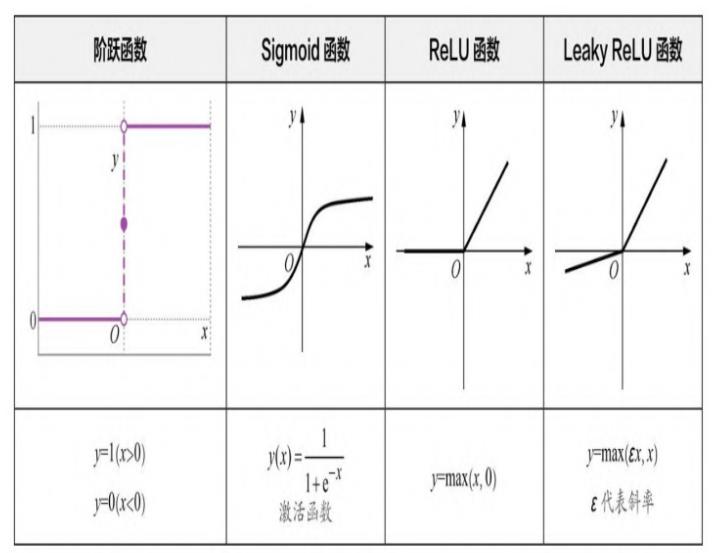
  还有一组函数在机器学习中相当重要，它们是神经网络中的激活函数（ activation function)。

  如下图所示。它们的作用是在机器学习算法中实现非线性的、阶跃性质的变换。其中的Sigmoid函数在机器学习的逻辑回归模型中起着重要的作用。

  

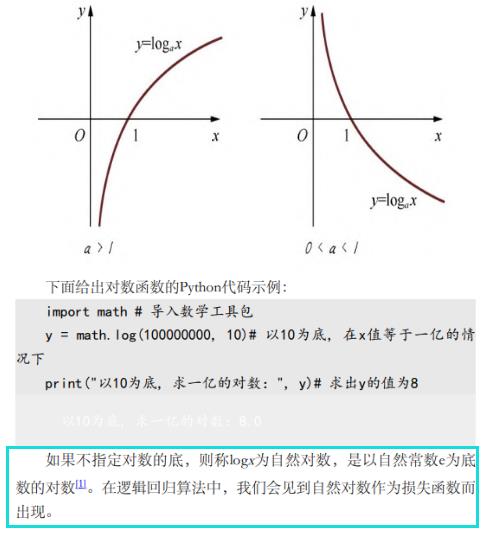
• 对数函数

  • 对数函数是指数函数（求幂)的逆运算。原来的指数就是对数的底。从几何意义上说，对数是将数轴进行强力的缩放，再大的数字经对数缩放都会变小。对数函数图像如下图所示。
  

2.2 捕捉函数的变化趋势

机器学习所关心的问题之一是捕捉函数的变化趋势，也就是研究y 如何随着x而变，这个趋势是通过求导和微分来实现的

2.3 梯度下降

• 对多元函数的各参数求偏导数, 然后把所求得的各个参数的偏导 数以向量的形式写出来, 就是梯度。

• 具体来说, 两个自变量的函数 $f\left(x_1,x_2\right)$, 对应着机器学习数据 集中的两个特征, 如果分别对 $x_1,x_2$ 求偏导数, 那么求得的梯度向量就 是 $\left(\partial f/\partial x_1,\partial f/\partial x_2\right){}^{\mathrm{T}}$, 在数学上可以表示成 $\Delta f\left(x_1,x_2\right)$ 。

• 那么计算梯度向量的意义何在呢? 其几何意义, 就是函数变化的 方向, 而且是变化最快的方向。

• 对于函数 f(x), 在点 $\left(x_0,y_0\right)$, 梯 度向量的方向也就是 y 值增加最快的方向。也就是说, 沿着梯度向量的方向 $\Delta f\left(x_0\right)$, 能找到函数的最大值。反过来说, 沿着梯度向量相反的方向, 也就是

  $-\Delta f\left(x_0\right)$ 的方向, 梯度减少最快, 能找到函数的最小值。

  如果某一个点的梯度向量的值为 0 , 那么也就是来到了导数为 0 的函数最低点（或局部最低点）了。

为什么不同教材中凸函数和凹函数的定义是不同的? - 秦浩然的回答 - 知乎 https://www.zhihu.com/question/31160556/answer/51276335

2.4 机器学习的数据结构–张量

• 在机器学习中，把用于存储数据的结构叫作张量(tensor) ，矩阵是二维数组，机器学习中就叫作2D张量

2.4.1 张量的轴、阶和形状

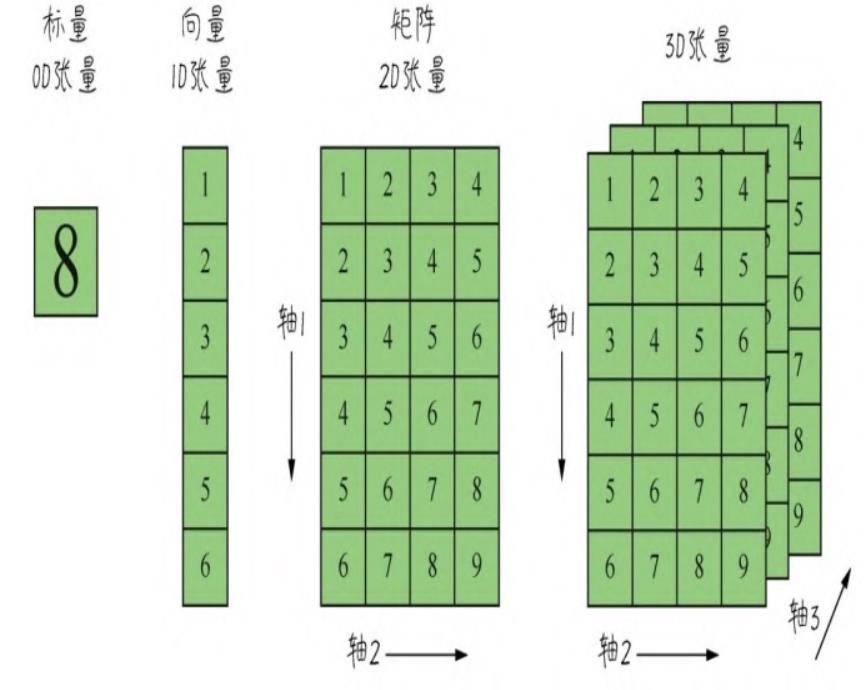
• 张量是机器学习程序中的数字容器，本质上就是各种不同维度的数组，如下图所示。我们把张量的维度称为轴( axis)(就是数学中的x轴，y轴，…….)，轴的个数称为阶(rank)(也就是俗称的维度，但是为了把张量的维度和每个阶的具体维度区分开，这里统一把张量的维度称为张量的阶。NumPy中把它叫作数组的轶)

  

• 张量的形状(shape）就是张量的阶，加上每个阶的维度（每个阶的元素数目)。

• 张量都可以通过NumPy来定义、操作。因此，把NumPy数学函数库里面的数组用好，就可以搞定机器学习里面的数据结构。

2.4.2 标量–0D(阶)张量

• 我们从最简单的数据结构开始介绍。仅包含一个数字的张量叫作标量（scalar），即0阶张量或0D张量。 标量的功能主要在于程序流程控制、设置参数值等。

• 下面创建一个NumPy标量

   import numpy as np #导入NumPy
   X = np.array(5) # 创建0D张量，也就是标量
   print("X的值",X)
   print("X的阶",X.ndim) #ndim属性显示张量轴的个数
   print("X的数据类型",X.dtype) # dtype属性显示张量数据类型
   print("X的形状",X.shape) # shape属性显示张量形状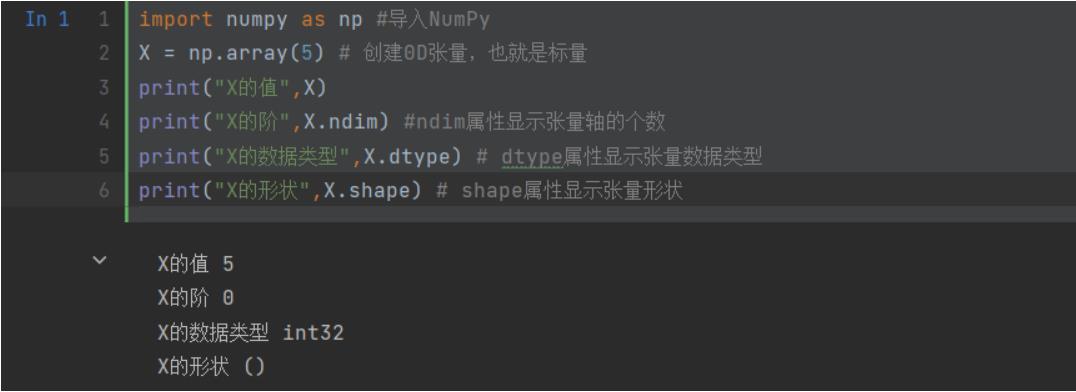
  

  

2.4.3 向量–1D(阶)张量

由一组数字组成的数组叫作向量（vector），也就是一阶张量，或称1D张量。一阶张量只有一个轴。

• 下面创建一个NumPy向量

   X = np.array([5,6,7,8,9]) #创建1D张量，也就是向量
   print("X的值",X)
   print("X的阶",X.ndim) #ndim属性显示张量轴的个数
   print("X的形状",X.shape) # shape属性显示张量形状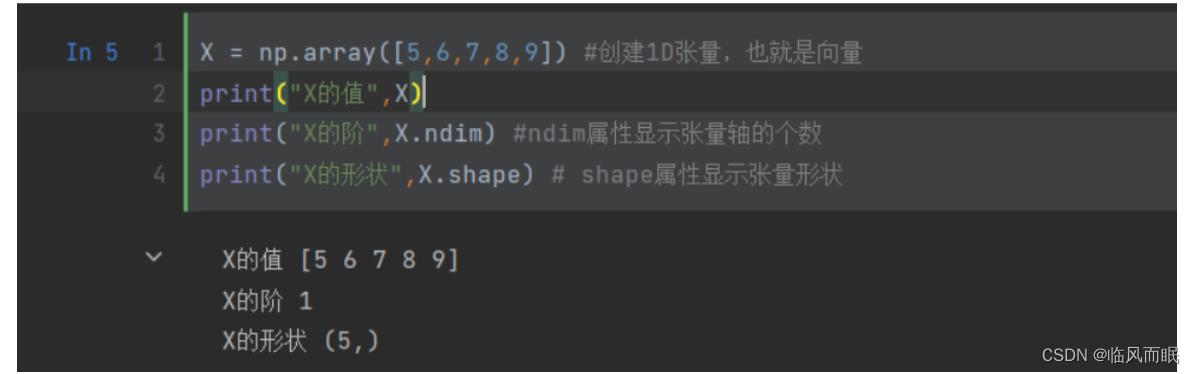
  

  

  • 创建向量的时候要把数字元素放进方括号里面，形成一个包含5个 元素的1D张量。需要再次强调的是，机器学习中把5个元素的向量称 为5维向量。千万不要把5维向量和5阶张量混淆

    • 上面这里是 ndim=1，1个轴，1阶张量， 有5个元素， 在这一阶有五个元素，是五维

  • 注意点1

  • 向量的维度

    • 这的确是机器学习过程中比较容易让人感到混乱的地方。其原因在于:维度（(dimensionality)(也就是英文字母D)可以表示沿着某个轴上的元素个数(如5D向量)，也可以表示张量中轴的个数（如5D张量)，这的确会令人感到混乱。还是那句话，为了区别两者，把5D张量称为5阶张量，而不称为5维张量。

  • 注意点2

  • 再看一下X向量的形状(5，)。这个描述方式也是让初学者比较困惑的地方，如果没有后面的逗号，可能看起来更舒服一点儿。但是我们要习惯，(5，)就表示它是一个1D张量，元素数量是5，也就是5维向量。

    • 下面这个语句又创建了一个向量，这个向量是一个1维向量:

        X= np.array([5])#1维向量，也就是1D数组里面只有一个元素
      

      • 这个语句和刚才创建标量的语句“X = np.array (5)”的唯一区别只是数字5被方括号括住了。正是因为这个方括号，这个语句创建出来的就不是数字标量，而是一个向量，即1D张量。它的轴的个数是1，形状是（1，) ，而不是()。
      

• 机器学习中的向量数据

  • 结合波士顿房价数据集来理解

     from keras.datasets import boston_housing # 波士顿房价数据集
     (X_train, y_train), (X_test, y_test) = boston_housing.load_data()
     print("X_train的形状：", X_train.shape)
     print("X_train中第一个样本的形状：", X_train[0].shape)
     print("y_train的形状：", y_train.shape)
    

    • 这个是Keras内置的波士顿房价数据集，是一个2D的普通数值数据集。

      
      • X_train是一个2D矩阵，是404个样本数据的集合。而y_train的形状，正是一个典型的向量，它是一个404维的标签向量。其实几乎所有的标签集的形状都是向量。

  • X_train[0]又是什么意思呢？它是X_train训练集的第一行数据， 这一行数据，是一个13维向量（也是1D张量）。也就是说，训练集的每行数据都包含13个特征。

• 向量的点积

• 两个向量之间可以进行乘法运算，而且不止一种，有点积( dotproduct)(也叫点乘）和叉积 （ cross product) (也叫叉乘)，其运算法则不同。机器学习中经常出现点积运算。
  $$\begin{gathered} \left[\begin{array}{c} \\ {a}_1\\ \\ a_2\\ \\ \cdot \\ \\ \cdot \\ \\ a_{n-1}\\ \\ a_n\end{array}\right]\cdot \left[\begin{array}{c} \\ {b}_1\\ \\ b_2\\ \\ \cdot \\ \\ \cdot \\ \\ b_{n-1}\\ \\ b_n\end{array}\right]=a_1{b}_1+a_2{b}_2+\cdots +a_{n-1}{b}_{n-1}+黄佳《零基础学机器学习》chap3笔记 \end{gathered}$$

  机器学习入门

  机器学习入门

  《从零开始：机器学习的数学原理和算法实践》chap1

  《深度学习入门基于python的理论与实现》chap2感知机 笔记

  零基础学Python--机器学习：人工智能与机器学习概述