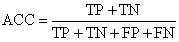机器学习中的评价指标

Posted 2023-03-25

作者 | 我的智慧生活 来源 | 咪付 在人工智能领域，机器学习的效果需要用各种指标来评价。本文将阐述机器学习中的常用性能评价指标，

参考技术A

作者 | 我的智慧生活

来源 | 咪付

在人工智能领域，机器学习的效果需要用各种指标来评价。本文将阐述机器学习中的常用性能评价指标，矢量卷积与神经网格的评价指标不包括在内。

训练与识别

当一个机器学习模型建立好了之后，即模型训练已经完成，我们就可以利用这个模型进行分类识别。

比如，给模型输入一张电动车的照片，模型能够识别出这是一辆电动车；输入一辆摩托车的照片，模型能够识别出这是一辆摩托车。前提是：在模型训练过程中，进行了大量电动车照片、摩托车照片的反复识别训练。

但即便模型具备了识别电动车、摩托车的能力，并不代表每次都能百分百正确识别。当然，我们肯定希望识别正确率越高越好。识别正确率越高，代表模型性能越良好。

具体有哪些指标可以评价模型性能的优良呢？我们从下面的例子来详细了解。

例如，一个测试样本集S总共有100张照片，其中，电动车的照片有60张，摩托车的照片是40张。给模型（二分类模型）输入这100张照片进行分类识别，我们的目标是：要模型找出这100张照片中的所有电动车。这里所说的目标即为正例（Positives），非目标即为负例（Negatives）。

假设模型给出的识别结果如下图：

从上表结果可以看出，在100张照片中，模型识别给出了50个电动车目标，剩下50个则是摩托车。这与实际的情况有出入（实际是：电动车60个，摩托车40个），因而有些识别是错误的。正确的识别数据体现在TP和TN（T代表True），错误的识别数据则体现在FP和FN（F代表False）。

在识别给出的50个电动车目标中，其中只有40个是对的（TP:真的电动车），另外10个则识别错了（FP:假的电动车，实际是摩托车）。

以上四个识别结果数值（TP、FP 、TN、FN）就是常用的评估模型性能优良的基础参数。在进一步详细说明TP、FP 、TN、FN各符号的含义之前，我们先来了解正例（正样本）、负例（负样本）的概念。

正例与负例

正例（Positives）：你所关注的识别目标就是正例。

负例（Negatives）：正例以外的就是负例。

例如，在上面的例子中，我们关注的目标是电动车，那么电动车就是正例，剩下摩托车则是负例。

再如，假设在一个森林里，有羚羊、驯鹿、考拉三种动物，我们的目标是识别出羚羊，那么羚羊就是正例，驯鹿和考拉则是负例。

又如，有一堆数字卡片，我们的目标是要找出含有数字8的卡片，那么含有数字8的卡片就是正例，剩于其他的都是负例。

混淆矩阵

了解了正例（Positives）和负例（Negatives）的概念，我们就可以很好地理解TP、FN、TN、FP的各自含义（其中T代表True，F代表False，P即Positives，N即Negatives）：

在以上四个基础参数中，真正例与真负例就是模型给出的正确的识别结果，比如电动车识别成电动车（真正例），摩托车识别成摩托车（真负例）；伪正例与伪负例则是模型给出的错误的识别结果，比如摩托车识别成电动车（伪正例），电动车识别成摩托车（伪负例）。其中，真正例（TP）是评价模型性能非常关键的参数，因为这是我们所关注的目标的有用结果，该值越高越好。

可以看出，在一个数据集里，模型给出的判断结果关系如下：

接下来，我们就来了解模型性能的各类评价指标。

模型性能指标

1、正确率（Accuracy）

正确率（Accuracy）：也即准确率，识别对了的正例（TP）与负例（TN）占总识别样本的比例。

即：

A=(TP+ TN)/S

在上述电动车的例子中，从上表可知，TP+ TN =70，S= 100，则正确率为：

A=70/100=0.7

通常来说，正确率越高，模型性能越好。

2、错误率（Error-rate）

错误率（Error-rate）：识别错了的正例（FP）与负例（FN）占总识别样本的比例。

即：

E=( FP+FN)/S

在上述电动车的例子中，从上表可知，FP+ FN =30，S= 100，则错误率为：

E=30/100=0.3

可见，正确率与错误率是分别从正反两方面进行评价的指标，两者数值相加刚好等于1。正确率高，错误率就低；正确率低，错误率就高。

3、精度（Precision）

精度（Precision）：识别对了的正例（TP）占识别出的正例的比例。其中，识别出的正例等于识别对了的正例加上识别错了的正例。

即：

P=TP/(TP+ FP)

在上述电动车的例子中，TP=40，TP+ FP=50。也就是说，在100张照片识别结果中，模型总共给出了50个电动车的目标，但这50个目标当中只有40个是识别正确的，则精度为：

P=40/50=0.8

因此，精度即为识别目标正确的比例。精度也即查准率，好比电动车的例子来说，模型查出了50个目标，但这50个目标中准确的比率有多少。

4、召回率（Recall）

召回率（Recall）：识别对了的正例（TP）占实际总正例的比例。其中，实际总正例等于识别对了的正例加上识别错了的负例（真正例+伪负例）。

即：

R=TP/(TP+ FN)

同样，在上述电动车的例子中，TP=40，TP+FN =60。则召回率为：

R=40/60=0.67

在一定意义上来说，召回率也可以说是“找回率”，也就是在实际的60个目标中，找回了40个，找回的比例即为：40/60。同时，召回率也即查全率，即在实际的60个目标中，有没有查找完全，查找到的比率是多少。

从公式可以看出，精度与召回率都与TP值紧密相关，TP值越大，精度、召回率就越高。理想情况下，我们希望精度、召回率越高越好。但单独的高精度或高召回率，都不足以体现模型的高性能。

例如下面的例子：

高精度模型

从上表可以看出，该模型识别结果给出正例50个，负例200个。在识别给出的50个正例当中全部都正确（都是真正例，没有伪正例），因而精度P为100%，非常高。但是识别给出的200个负例全部都错误（都是伪负例），错误率非常高，这样的模型性能其实非常低。

高召回率模型

上表可以看出，该模型识别结果给出正例110个，负例0个。在110个正例当中，其中10个是真正例（识别正确），100个却是伪正例（识别错误）。在这个测试数据集中，计算的召回率R为100%，非常好，也就是说，在这个数据集里总共有10个目标，已全部找到（召回）。但同时，计算得出模型识别结果的错误率E也很高，高达91%，所以这个模型性能也很低，基本不可靠。

5、精度-召回率曲线（PR曲线）

实际中，精度与召回率是相互影响的。通常，精度高时，召回率就往往偏低，而召回率高时，精度则会偏低。这其实也很好理解，前面我们说了，精度即查准率，召回率即查全率，要想查得精准（一查一个准），即模型给出的目标都正确，那就得提高阈值门槛，阈值一提高，符合要求的目标就会减少，那必然会导致漏网之鱼增多，召回率降低。

相反，若想召回率高，没有漏网之鱼（目标都找到），就要降低阈值门槛，才能把所有目标收入囊中，与此同时会揽入一些伪目标，从而导致精度降低。

例如，在不同的阈值下（分别为0.6和0.5），模型给出15张图片的识别结果如下：

上表中1、0分别代表正例和负例。通过设定一个阈值（T），当置信度分数大于阈值则识别为正例，小于阈值则识别为负例。上表识别结果中当阈值T=0.6，模型给出的正例有8个，当阈值T=0.5，模型给出的正例则有10个。

通过与真实属性值核对，我们可以得出这两个阈值下的各个参数（TP、FP、FN）以及计算得出召回率（R）和精度（P）如下：

可以看出，设定的阈值不同，得出的召回率（R）和精度（P）也不相同。因此，对于每一个阈值可得到对应的一组（R，P），例如，上述的两个阈值可得出两组（R，P），分别为：（0.86，0.75）和（1，0.7）。如果取多个不同的阈值，就可以得到多组（R，P）。将这些坐标点（R，P）绘制在坐标上，然后将各坐标点用曲线连起来，即可得到PR曲线。

因此，PR曲线即是以召回率R为横轴，精度P为纵轴画出的曲线，如下图：

6、AP（Average Precision）值

PR曲线下的面积称为AP（Average Precision），表示召回率从0-1的平均精度值。如何计算AP呢？很显然，根据数学知识，可用积分进行计算，公式如下：

显然，这个面积的数值不会大于1。PR曲线下的面积越大，模型性能则越好。性能优的模型应是在召回率（R）增长的同时保持精度（P）值都在一个较高的水平，而性能较低的模型往往需要牺牲很多P值才能换来R值的提高。如下图所示，有两条PR曲线，可以看出，PR1曲线为性能较优的模型表现形式，PR1曲线下的面积明显大于PR2曲线下的面积。对于PR1曲线，随着R值的增长，P值仍能保持在一个较高的水平；而对于PR2曲线，随着R值的增长，P值则不断下降，因此是通过牺牲P值才能换得R值的提高。

除了使用积分方法计算AP值，实际应用中，还常使用插值方法进行计算。常见的一种插值方法是：选取11个精度点值，然后计算出这11个点的平均值即为AP值。

怎样选取11个精度点值呢？通常先设定一组阈值,例如[0,0.1,0.2…,1], 对于R大于每一个阈值（R>0, R>0.1,…, R>1），会得到一个对应的最大精度值Pmax,这样就会得到11个最大精度值（Pmax1, Pmax2,…, Pmax11）。

则：

AP=（Pmax1+ Pmax2+…+ Pmax11）/11

7、mAP（Mean Average Precision）值

AP是衡量模型在单个类别上平均精度的好坏，mAP则是衡量模型在所有类别上平均精度的好坏，每一个类别对应有一个AP，假设有n个类别，则有n个AP，分别为：AP1，AP2，…，APn, mAP就是取所有类别 AP 的平均值，即：

mAP= (AP1+ AP2+…+ APn)/n

8、综合评价指标F-Measure

F-Measure又称F-Score，是召回率R和精度P的加权调和平均，顾名思义即是为了调和召回率R和精度P之间增减反向的矛盾，该综合评价指标F引入了系数α对R和P进行加权调和，表达式如下：

而我们最常用的F1指标，就是上式中系数α取值为1的情形，即：

F1=2P.R/(P+R)

F1的最大值为1，最小值为0。

9、ROC曲线与AUC

ROC(Receiver Operating Characteristic)曲线与AUC(Area Under the Curver)

ROC曲线，也称受试者工作特征。ROC曲线与真正率（TPR，True Positive Rate）和假正率(FPR, False Positive Rate)密切相关。

真正率(TPR): 识别对了的正例（TP）占实际总正例的比例，实际计算值跟召回率相同。即：

TPR =TP/(TP+ FN)

假正率(FPR): 识别错了的正例（FP）占实际总负例的比例。也可以说，误判的负例（实际是负例，没有判对）占实际总负例的比例。计算式如下：

FPR =FP/(FP+ TN)

以FPR为横轴，TPR为纵轴，绘制得到的曲线就是ROC曲线，绘制方法与PR曲线类似。绘制得到的ROC曲线示例如下：

一般来说，ROC曲线越靠近左上方越好。

ROC曲线下的面积即为AUC。面积越大代表模型的分类性能越好。如上图所示，绿线分类模型AUC=0.83大于红线分类模型AUC=0.65，因此，绿线分类模型的分类性能更优。并且，绿线较红线更光滑。通常来说，ROC曲线越光滑，过拟合程度越小。绿线分类模型的整体性能要优于红线分类模型。

10、IoU（Intersection-over-Union）指标

IoU简称交并比，顾名思义数学中交集与并集的比例。假设有两个集合A与B, IoU即等于A与B的交集除以A与B的并集，表达式如下：

IoU=A∩B/A∪B

在目标检测中，IoU为预测框(Prediction)和真实框(Ground truth)的交并比。如下图所示，在关于小猫的目标检测中，紫线边框为预测框(Prediction)，红线边框为真实框(Ground truth)。

将预测框与真实框提取如下图，两者的交集区域为左下图斜线填充的部分，两者的并集区域为右下图蓝色填充的区域。IoU即为：

左边斜线填充的面积/右边蓝色填充的总面积。

预测框与真实框交集与并集示例

在目标检测任务中，通常取IoU≥0.5，认为召回。如果IoU阈值设置更高，召回率将会降低，但定位框则更加精确。

理想的情况，当然是预测框与真实框重叠越多越好，如果两者完全重叠，则交集与并集面积相同，此时IoU等于1。

11、Top1与TopK

Top1：对一张图片，模型给出的识别概率中（即置信度分数），分数最高的为正确目标，则认为正确。这里的目标也就是我们说的正例。

TopK: 对一张图片，模型给出的识别概率中（即置信度分数），分数排名前K位中包含有正确目标（正确的正例），则认为正确。

K的取值一般可在100以内的量级，当然越小越实用。比如较常见的，K取值为5，则表示为Top5，代表置信度分数排名前5当中有一个是正确目标即可；如果K取值100，则表示为Top100，代表置信度分数排名前100当中有一个是正确目标（正确的正例）即可。可见，随着K增大，难度下降。

例如，在一个数据集里，我们对前5名的置信度分数进行排序，结果如下：

上表中，取阈值T=0.45，排名前5的置信度分数均大于阈值，因此都识别为正例。对于Top1来说，即ID号为4的图片，实际属性却是负例，因此目标识别错误。而对于Top5来说，排名前5的置信度分数中，有识别正确的目标，即ID号为2、20的图片，因此认为正确。

在常见的人脸识别算法模型中，正确率是首当其冲的应用宣传指标。事实上，对同一个模型来说，各个性能指标也并非一个静止不变的数字，会随着应用场景、人脸库数量等变化而变化。因此，实际应用场景下的正确率跟实验室环境下所得的正确率一定是存在差距的，某种程度上说，实际应用场景下的正确率更具有评价意义。

机器学习算法中的评价指标（准确率召回率F值ROCAUC等）

参考链接：https://www.cnblogs.com/Zhi-Z/p/8728168.html

具体更详细的可以查阅周志华的西瓜书第二章，写的非常详细~

一、机器学习性能评估指标

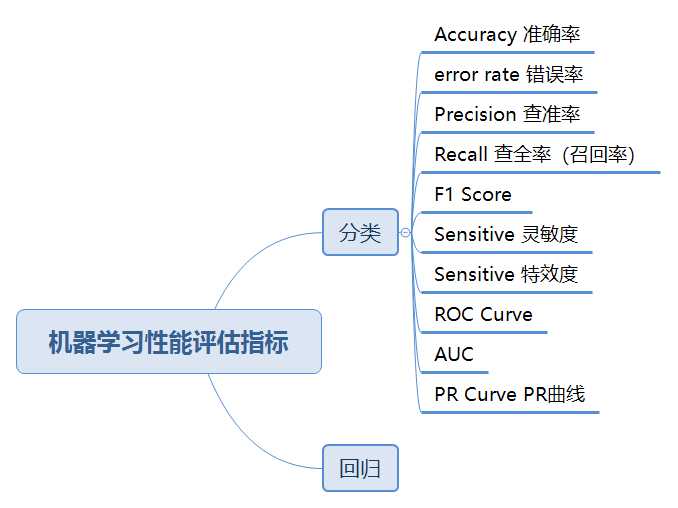
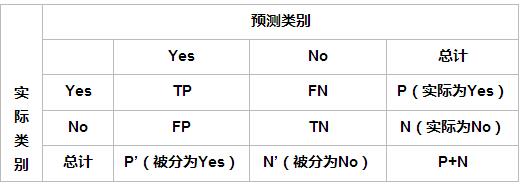
1.准确率(Accurary)

 

准确率是我们最常见的评价指标，而且很容易理解，就是被分对的样本数除以所有的样本数，通常来说，正确率越高，分类器越好。

准确率确实是一个很好很直观的评价指标，但是有时候准确率高并不能代表一个算法就好。比如某个地区某天地震的预测，假设我们有一堆的特征作为地震分类的属性，类别只有两个：0：不发生地震、1：发生地震。一个不加思考的分类器，对每一个测试用例都将类别划分为0，那那么它就可能达到99%的准确率，但真的地震来临时，这个分类器毫无察觉，这个分类带来的损失是巨大的。为什么99%的准确率的分类器却不是我们想要的，因为这里数据分布不均衡，类别1的数据太少，完全错分类别1依然可以达到很高的准确率却忽视了我们关注的东西。再举个例子说明下。在正负样本不平衡的情况下，准确率这个评价指标有很大的缺陷。比如在互联网广告里面，点击的数量是很少的，一般只有千分之几，如果用acc，即使全部预测成负类（不点击）acc也有 99% 以上，没有意义。因此，单纯靠准确率来评价一个算法模型是远远不够科学全面的。

2、错误率（Error rate）

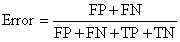
错误率则与准确率相反，描述被分类器错分的比例，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 - error rate。

3、查准率（Precision）

查准率(precision)定义为：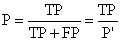 

表示被分为正例的示例中实际为正例的比例。

4、查全率（召回率）（recall）

 

召回率是覆盖面的度量，度量有多个正例被分为正例，recall=TP/(TP+FN)=TP/P=sensitive，可以看到召回率与灵敏度是一样的。

5、综合评价指标（F-Measure）

 P和R指标有时候会出现的矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure（又称为F-Score）。 F-Measure是Precision和Recall加权调和平均： 
 

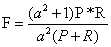
当参数α=1时，就是最常见的F1，也即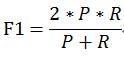 
 
可知F1综合了P和R的结果，当F1较高时则能说明试验方法比较有效。

6、灵敏度（sensitive）

sensitive = TP/P，表示的是所有正例中被分对的比例，衡量了分类器对正例的识别能力。

7、特效度（sensitive）

specificity = TN/N，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力。

 8、其他评价指标

8.1 ROC曲线

ROC（Receiver Operating Characteristic）曲线是以假正率（FP_rate）和真正率（TP_rate）为轴的曲线，ROC曲线下面的面积我们叫做AUC，如下图所示

 

，

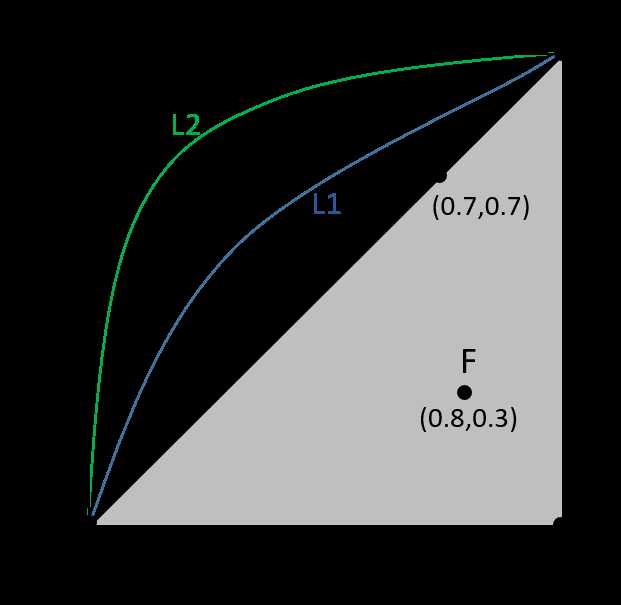
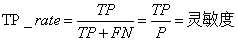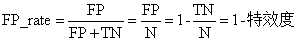
（1）曲线与FP_rate轴围成的面积（记作AUC）越大，说明性能越好，即图上L2曲线对应的性能优于曲线L1对应的性能。即：曲线越靠近A点（左上方）性能越好，曲线越靠近B点（右下方）曲线性能越差。 
（2）A点是最完美的performance点，B处是性能最差点。 
（3）位于C-D线上的点说明算法性能和random猜测是一样的，如C、D、E点；位于C-D之上（曲线位于白色的三角形内）说明算法性能优于随机猜测，如G点；位于C-D之下（曲线位于灰色的三角形内）说明算法性能差于随机猜测，如F点。 
（4）虽然ROC曲线相比较于Precision和Recall等衡量指标更加合理，但是其在高不平衡数据条件下的的表现仍然不能够很好的展示实际情况。

8.2、PR曲线： 
即，PR（Precision-Recall），以查全率为横坐标，以查准率为纵坐标的曲线。 
举个例子（例子来自Paper：Learning from eImbalanced Data）： 

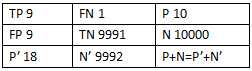
假设N>>P（即Negative的数量远远大于Positive的数量），就算有较多N的sample被预测为P，即FP较大为9，但是由于N很大，FP_rate的值仍然可以很小0.9%，TP_rate=90%（如果利用ROC曲线则会判断其性能很好，但是实际上其性能并不好），但是如果利用PR，P=50%，R=90%，因此在极度不平衡的数据下（Positive的样本较少），PR曲线可能比ROC曲线更实用。