（翻）为什么要训练人工神经网络
Posted PacosonSWJTU
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了（翻）为什么要训练人工神经网络相关的知识，希望对你有一定的参考价值。
【README】
本文翻译自
https://towardsdatascience.com/how-do-we-train-neural-networks-edd985562b73【1】介绍
今天我将从非常简短的神经网络介绍开始，这足以理解我将要讨论的概念。 我将解释什么是损失函数以及“训练”神经网络或任何其他机器学习模型意味着什么。 我并不声称我的解释是对神经网络的完整、深入的介绍，事实上，希望您已经熟悉这些概念。 如果您想更好地了解神经网络中发生的事情，我会在文章末尾提供一个资源列表供您学习。
我将解释几年前在 kaggle 上运行的狗对猫比赛的例子。 在比赛中，我们面临的任务是识别给定图像上出现的是狗还是猫。
【2】定义神经网络
人工神经网络 (ANN) 的灵感来自于你大脑中实际发生的事情。 虽然这些类比非常松散，但人工神经网络与其生物学上的“父母”有几个相似之处。 它们由一定数量的神经元组成。 因此，让我们看一下单个神经元。
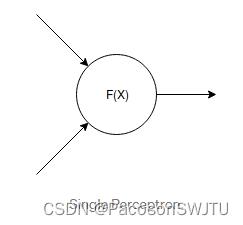
【图1】 神经元
我们将考虑弗兰克·罗森布拉特在 1957 年提出的最简单的神经元模型的稍微修改版本，称为“感知器”。 我所做的所有修改都是为了简单起见，因为我不会深入解释神经网络。 我只是想让你直观地了解正在发生的事情。
【2.1】什么是神经元？
它是一个数学函数。 它需要几个数字作为输入（任意数量）。 我上面画的神经元需要两个数字作为输入。 我们将每个输入数字表示为 xₖ，其中 k 代表输入索引。 对于每个输入 xₖ，神经元分配另一个数字 wₖ。 由这些数字组成的向量 wₖ 称为权重向量。 这些权重使每个神经元都独一无二。 它们在测试期间是固定的，但在训练期间，我们将更改这些数字以“调整”我们的网络（修改权值）。 我会在后面的帖子中谈到它。 正如我上面所说，
1）定义：神经元是一个函数，是权重和输入的线性组合，在其上带有某种非线性函数；神经元就包括了 线性与非线性部分了 ；
【2.2】线性部分
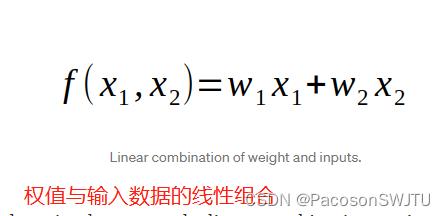
【公式1】 权值与输入数据的线性组合
上面的公式就是我所说的线性组合。 我们将获取输入，将它们乘以相应的权重并将所有内容相加。 结果是一个数字。
【2.3】非线性部分
最后一部分——是在它上面应用某种非线性函数。
本文使用的最流行的非线性实际上比称为整流线性单元 (ReLU)（或 修正线性单元，Rectified Linear Unit ） 的线性函数更容易。 公式如下：
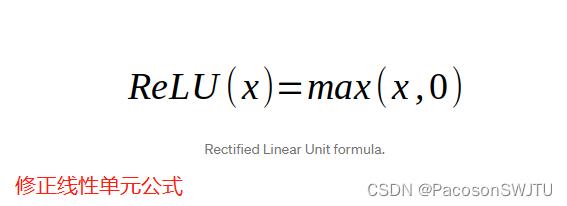
【公式2】 修正（整流）线性单元公式
1）整流（修正）线性单元公式描述
如果我们的数字大于零，那么我们将按原样采用该数字；
如果它小于零，那么我们将采用零。
2）激活函数：这种应用于神经元顶部线性的非线性函数称为激活函数。 我们必须有某种非线性函数的原因将在后面阐述。
总而言之，神经元是一个函数，它接受一些固定数量的输入并输出一个数字——它的激活。
3）神经元最终公式如下：
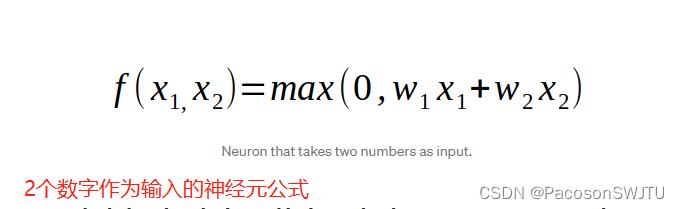
【公式3】 神经元公式
提前一点，如果我们以狗和猫为例，我们将把我们的图像作为输入传递给神经元。 您可能想知道，当我将神经元定义为函数时，我们如何传递图像。 您应该记住，我们在计算机中存储图像的方式是将其表示为一个数字数组，每个数字表示给定像素的亮度。 因此，将其传递给神经元的方法是获取该 2D 数组（或在彩色图像的情况下为 3D），将其连续展平以获得 1D 向量并将所有这些数字传递给神经元。
不幸的是，它使我们的神经网络依赖于图像大小，我们只能处理由神经网络定义的给定大小的图像。 现代神经网络已经找到了解决这个问题的方法，但本文我们将有这个限制，为了简化问题。
【2.4】神经网络举例
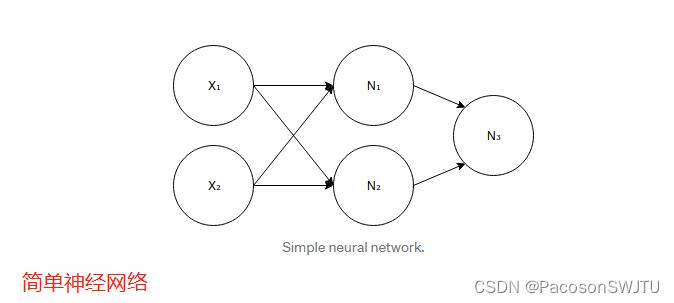
【图2】 简单神经网络
上面定义的网络有 5 个神经元。如您所见，这些神经元堆叠在 3 个完全连接的层中，即一层的每个神经元都连接到下一层的每个神经元。网络中有多少层，每层中有多少神经元以及它们如何连接——所有这些选择都定义了神经网络的架构（结构）。
1）第一层：第一层由 2 个神经元组成，称为输入层。这一层中的神经元实际上并不是我之前描述的神经元，从某种意义上说，它们不执行任何计算。它们仅用于表示网络的输入。
2）对非线性的需求来自这样一个事实：即我们将神经元连接在一起，并且线性函数之上的线性函数本身就是一个线性函数。因此，如果没有在每个神经元中应用非线性函数，则神经网络将是线性函数，因此不会比单个神经元强大。
最后要注意的是，我们通常想要一个介于 0 和 1 之间的数字作为输出神经网络的输出，以便我们将其视为概率。例如，在 dog-vs-cats 中，我们可以将接近零的数字视为猫，将接近一的数字视为狗。为此，我们将对最后一个神经元应用不同的激活函数。
3）我们将使用 sigmoid 激活：关于这个函数，你唯一需要知道的是它返回一个从 0 到 1 的数字，这正是我们想要的。说了这么多，我们准备定义一个与我上面画的网络相对应的函数：
【公式4】 神经网络函数
定义了神经网络的函数。
w 的上标表示神经元的索引（第几个神经元）； 如图2 中的神经元N的索引；
w 的下标表示输入数据的索引； 如图2中的输入数据X的索引；
4）小结：
因此，我们有了某种函数，可以定义神经网络 如 f(x1, x2) ，它接受一些数字并输出另一个介于 0 和 1 之间的数字。
这个函数有什么公式实际上并不重要，重要的是我们通过一些权值把复杂的非线性函数参数化，从某种意义上说，我们可以通过改变权重来改变这个函数（神经网络函数）。
【3】损失函数（神经网络效果的度量函数）
在我开始谈论训练之前，唯一需要定义的是损失函数。
1）损失函数定义：是一个函数，它告诉我们，我们的神经网络对某项任务有多好（衡量神经网络的效果）。 直观的做法是，获取每个训练示例，通过神经网络获取数字，从我们想要获得的实际数字（真实值）中减去它并平方它（因为负数与正数一样糟糕）。
即：用真实值减去神经网络输出值 并开平方；
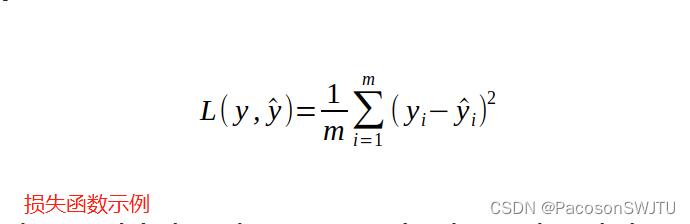
【图3】 损失函数示例
其中 y 代表我们想从网络中获取的数字，y（带帽子） 代表我们通过网络传递示例实际得到的数字，i - 训练示例的索引。 即 y是真实值，y帽子 是神经网络输出结果；需要对两者做比较；
【例】再次以狗对猫为例。
有一个狗和猫的图片数据集，如果是狗，则标记为 1，如果是猫，则标记为 0。 这个标签对应于 y——当我们将图像传递给它时，它是我们想要从网络获取的数字（y）。
为了计算损失函数，我们将遍历数据集中的每个训练示例，计算该示例的 y，然后计算上面定义的函数。 如果损失函数很大，那么我们的神经网络表现不佳，我们希望数字尽可能小。
我们可以重写这个公式，将 y 更改为我们网络的实际函数，以更深入地了解损失函数和神经网络的联系。
【4】训练
当我们从神经网络开始时，我们随机初始化我们的权重。显然，它不会给你带来很好的结果。在训练过程中，我们希望从性能不佳的神经网络开始，并以高精度的网络结束。
在损失函数方面，我们希望我们的损失函数在训练结束时要低得多。改进网络是可能的，因为我们可以通过调整权重来改变它的功能。我们希望找到另一个比最初的函数执行得更好的函数。
训练问题等价于最小化损失函数的问题。为什么要最小化损失而不是最大化？原来损失是更容易优化的功能。
有很多优化函数的算法。这些算法可以基于或不基于梯度，从某种意义上说，它们不仅使用函数提供的信息，还使用其梯度。最简单的基于梯度的算法称为随机梯度下降。让我们看看它是如何工作的。
【4.1】随机梯度下降
首先，我们需要记住关于某个变量的导数是什么。 让我们采用一些简单的函数 f(x) = x。 如果我们记得我们知道的高中微积分规则，那么它的导数在 x 的每个值上都是一个。 它告诉我们什么？ 导数是当我们向正方向迈出无限小步时函数变化的速度。 在数学上它可以写成以下形式：
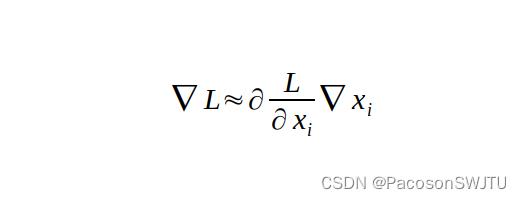
这意味着：我们的函数变化量（左项）大约等于对某个变量 x 的导数乘以x变化量。
当我们采取的步骤无限小时，该近似值将是准确的，这是导数的非常重要的概念。
1）简单导数 f(x) = x
回到我们的简单函数 f(x) = x，我们说我们的导数是 1，这意味着，如果在正方向上采取一些步骤 epsilon（变量名 ε），函数输出将乘以 1 乘以我们的 step epsilon，这就是 ε。 这实际上甚至不是一个近似值，这是准确的。 为什么 ？ 因为我们的导数对于 x 的每个值都是相同的。 对于大多数功能来说，情况并非如此。
2）复杂导数 f(x) = x^2
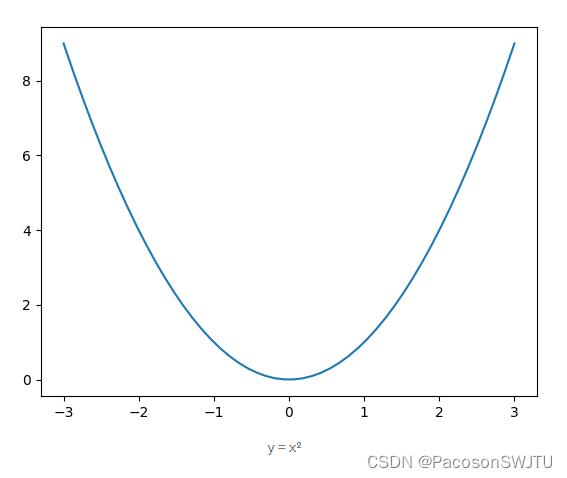
从微积分规则我们知道，该函数的导数是 2x。 如果我们从 x 的某个值开始并进行一些步骤 epsilon，那么我们的函数更改了多少将不会完全等于上面给出的公式。
现在，梯度是偏导数的向量，其元素包含关于函数所依赖的某个变量的导数。 对于我们目前考虑的简单函数，这个向量只包含一个元素，因为我们只使用了接受一个输入的函数。 对于更复杂的函数（比如我们的损失函数），梯度将包含关于我们想要的每个变量的导数。
我们如何使用 导数 为我们提供的这些信息，以最小化某些函数？
让我们回到函数 f(x) = x²。显然，该函数的最小值在 x = 0 处，但计算机怎么知道呢？
假设我们从 x 的某个随机值开始，该值为 2。函数在 x = 2 中的导数等于 4。这意味着我们朝正方向迈出一步，我们的函数将按比例更改为 4。所以会增加。相反，我们想要最小化我们的函数，所以我们可以朝相反的方向迈出一步，负的，以确保我们的函数会减少，至少一点点。我们能迈出多大的一步？好吧，这是个坏消息。我们的导数只保证如果采取无限小的步长，函数会减小。我们不能那样做。通常，您希望使用某种超参数来控制步长的大小。这个超参数称为学习率，我稍后会谈到。现在让我们看看如果我们从点 x = -2 开始会发生什么。导数现在等于 -4，这意味着，如果在正方向上迈出一小步，我们的函数将与 -4 成比例地变化，因此它会减小。这正是我们想要的。
注意到这里的模式了吗？当x > 0，我们的导数大于零，我们需要往负方向走，当x < 0，我们的导数小于零，我们需要往正方向走。我们总是需要朝着与导数相反的方向迈出一步。让我们将相同的想法应用于渐变。
梯度是指向空间中某个方向的向量。它实际上指向了函数增长最快的方向。由于我们想要最小化我们的函数，我们将朝着梯度的相反方向迈出一步。让我们应用我们的想法。
【梯度下降】
在神经网络中，我们将输入 x 和输出 y 视为固定数字。我们将要对其进行导数的变量是权重 w，因为这些是我们想要更改以改进我们的神经网络的输出值。如果我们根据权重计算损失函数的梯度，并在梯度的相反方向上采取小步骤，我们的损失将逐渐减少，直到收敛到某个局部最小值。这种算法称为梯度下降。在梯度下降的每次迭代中更新权重的规则如下：
【学习率】
上述符号中的 lr 表示学习率。它可以控制我们在每次迭代中采取的步骤的大小。
它是训练神经网络时要调整的最重要的超参数。如果你选择了太大的学习，那么你会做出太大的步骤，并且会“跳过”最小值。这意味着你的算法会发散。如果您选择的学习率太小，可能需要太多时间才能收敛到某个局部最小值。人们已经开发了一些非常好的技术来找到最佳学习率，但这超出了本文的范围。其中一些在我的另一篇文章“改进我们使用学习率的工作方式”中进行了描述。
https://techburst.io/improving-the-way-we-work-with-learning-rate-5e99554f163b
不幸的是，我们不能真正应用这种算法来训练神经网络，原因在于我们的损失函数公式。
【小批量梯度下降】
从我们上面定义的内容可以看出，我们的公式是总和的平均值。从微积分我们知道，和的导数是导数的和。因此，为了计算损失的导数，我们需要遍历数据集的每个示例。在梯度下降的每次迭代中都这样做是非常低效的，因为算法的每次迭代只会将我们的损失提高一小步。为了解决这个问题，还有另一种算法，称为 Mini-batch Gradient Descent（小批量梯度下降）。更新权重的规则保持不变，但我们不会计算精确的导数。相反，我们将在数据集的一些小型 mini-batch 上近似导数，并使用该导数来更新权重。
小批量不能保证朝着最佳方向采取措施。事实上，它通常不会。使用梯度下降，如果选择足够小的学习率，保证每次迭代你的损失都会减少。对于小批量，这是不正确的。您的损失会随着时间的推移而减少，但会波动并且更加“嘈杂”。
【估计导数批次大小】
用于估计导数的批次大小是您必须选择的另一个超参数。 通常，您希望您的内存可以处理尽可能大的批量大小。 但我很少看到有人使用比 100 大得多的批大小。
批次大小等于 1 的小批量梯度下降的极端版本称为随机梯度下降。 在现代文献中并且非常普遍地，当人们说随机梯度下降（SGD）时，他们实际上指的是小批量梯度下降。 大多数深度学习框架都允许您为 SGD 选择批量大小。
【梯度下降及变体】
最近，越来越多的人一直在使用更高级的算法。 它们中的大多数是基于梯度的，实际上是基于 SGD 并稍作修改。 我也打算写这些。
【4】反向传播
【如何计算损失函数梯度】
关于基于梯度的算法，唯一要说的是我们如何计算梯度。 最快的计算方法是分析地找到每个神经网络架构的导数。 我想，当谈到神经网络时，我不应该说这是一个疯狂的想法。 我们上面为一个非常简单的神经网络定义的公式很难找到所有导数，而且我们只有 6 个参数。 现代建筑有数百万个。
第二种方法，事实上也是最容易实现的，是用我们从微积分中知道的以下公式来近似导数：
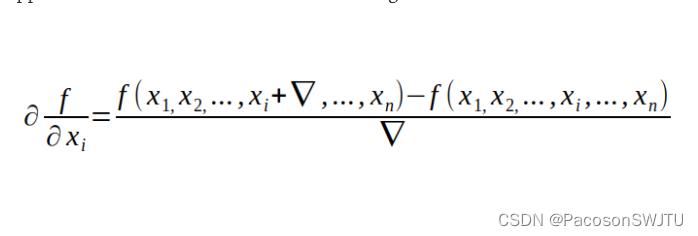
虽然它非常容易实现，但这样做的计算成本太高了。
计算导数的最后一种方法称为反向传播，它可以很好地平衡计算难度和计算成本。 讨论这个算法超出了本文的范围，但如果你想了解更多关于它的信息，请转到本文的最后一部分，我列出了一些资源来了解更多关于神经网络的信息。
【5】为什么会起作用
当我第一次了解神经网络及其工作原理时，我理解了所有的方程式，但我不太确定它们为什么会起作用。我们可以采用一些函数，然后采用一些导数并最终得到可以在图像上区分狗和猫的算法，这对我来说似乎有点超现实。为什么我不能给你一个很好的直觉，为什么神经网络工作得这么好，有一些方面你应该注意。
1）我们用神经网络解决的任何问题都必须以某种数学方式表达。对于狗和猫，情况如下：我们需要找到一个函数，它从图像中获取所有数字并输出它是狗的概率。您实际上可以通过这种方式定义任何分类问题。
2）可能不清楚，为什么会有这样一个函数可以在给定的图像上区分狗和猫。这里的想法是，只要你有一些带有输入和标签的数据集，总会有一个函数在给定的数据集上运行良好。问题是该功能将非常复杂。神经网络可以提供帮助。有一个“通用逼近定理”，它说只有一个隐藏层的神经网络可以尽可能好地逼近任何函数。现在，尚不清楚为什么，即使我们找到了该函数的近似值，它在一个新数据集上的工作效果也一样好，这是一个神经网络在训练期间没有看到的。这被称为泛化问题，它是一个开放的研究问题。研究表明，SGD 具有“自我泛化”效应。但是我们仍然不能很好地理解这个问题。
创作打卡挑战赛
赢取流量/现金/CSDN周边激励大奖
以上是关于（翻）为什么要训练人工神经网络的主要内容，如果未能解决你的问题，请参考以下文章