[人工智能-深度学习-14]:神经网络基础 - 常见loss损失函数之逻辑分类,对数函数,交叉熵函数
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[人工智能-深度学习-14]:神经网络基础 - 常见loss损失函数之逻辑分类,对数函数,交叉熵函数相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120559396
目录
第1章 什么损失函数
1.1 什么是机器学习
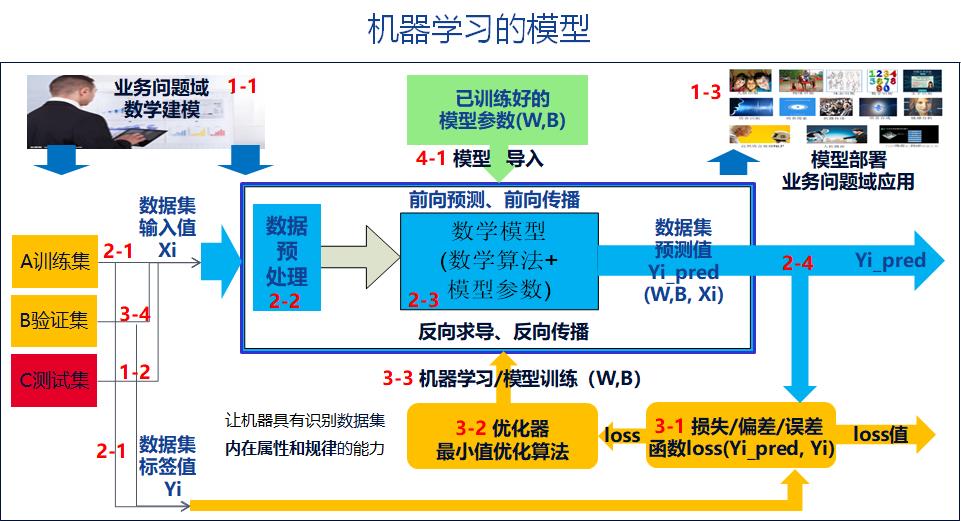
[人工智能-深度学习-8]:神经网络基础 - 机器学习、深度学习模型、模型训练_文火冰糖(王文兵)的博客-CSDN博客
1.2 什么是监督式机器学习
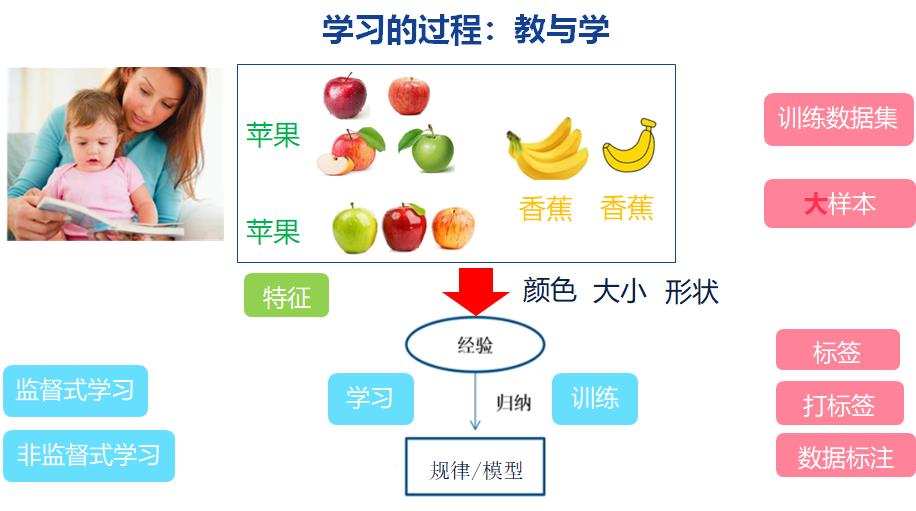
百度百科:监督式学习(英语:Supervised learning),是一个机器学习中的方法,可以由训练资料中学到或建立一个模式(函数 / learning model),并依此模式推测新的实例。
训练资料是由输入物件(通常是向量)和预期输出所组成。
函数的输出可以是一个连续的值(称为回归分析),或是预测一个分类标签(称作分类)。
白话:所谓监督室式学习,给定的数据集和对应的标准答案,即标签。让机器以后的数据集合标准答案进行学习。
其中,数据集用{Xi}表示,对应的标签值,又称为样本值,期望值,用{Yi} 表示。
神经网络模型,利用当前的参数,对对数据集{Xi}进行运算和预测,获得的输出值为{Yi_pred}.
也就是说,监督室学习,是指有标准答案的学习。
标准答案的形式:
- 标签值
- 样本值
备注:标签值、样本值、期望值,并不是没有任何错误的值期望值,而是人为的采样值,是表面现象下参考值,并不一定是内涵的规律值。
1.3 OneHot编码
1.4 什么是损失函数
监督学习本质上是给定一系列训练样本 {Xi},尝试学习样本的映射关系 {Xi -> Yi},使得给定一个 x_real,即便这个 x_real不在训练样本{Xi -> Yi}中,也能够得到其输出值{Y_pred}尽量接近真实{Y_real}的输出。
损失函数(Loss Function)则是这个过程中关键的一个组成部分,用来衡量模型的预测输出{Y_pred}与样本真实值{Yi}的之间的差距,并给模型的优化指明方向:针对给定的样本{Xi},其误差最小,即预测输出{Y_pred}与样本真实值{Yi}尽可能的接近,尽可能的相似。loss值越小,相似度越高,误差越小。
在实际工程中,由于{Y_real}是未知的,因此,在监督式学习中,使用样本标签{Yi}作为样本数据集{Xi}的真实值!!!!
由于实际样本数据集不是单个数据,因此,loss函数实际是所有样本误差的平均,反映的是模型对样本数据集中所有样本的预测映射关系 {Xi -> Yi_pred},与已知的样本标签的映射关系{Xi -> Yi_pred}整体的相似程度,而不是单个样本的相似程度!!!!
 在相同的应用场合,描述相似程度的loss数学函数不尽同。
在相同的应用场合,描述相似程度的loss数学函数不尽同。
在不同的应用场合,描述相似程度的loss数学函数不尽同。
因此就有各种不同的loss函数,如均方差损失 Mean Squared Loss、平均绝对误差损失 Mean Absolute Error Loss、Huber Loss、分位数损失 Quantile Loss、交叉熵损失函数 Cross Entropy Loss、Hinge 损失 Hinge Loss。
不同的损失函数的基本的函数表达式、原理、特点并不相同方面。
因此,损失函数研究的是:如何表达两个函数(X-Y的映射关系称为函数)之间的相似程度的数学表达式。
因此,损失函数研究的是:如何表达两个函数(X-Y的映射关系称为函数)之间的距离远近的数学表达式。
损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别,结构风险损失函数是指经验风险损失函数加上正则项.
损失函数用来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。不同的模型用的损失函数一般也不一样。
1.5 本文重点阐述:
用于逻辑分类相关的损失函数:0-1损失函数,log损失函数,交叉熵损失函数等。
备注: 在本文中 Yi_pred也表示为
第2章 二/多元分类损失函数
2.1 二/多元分类损失函数模型
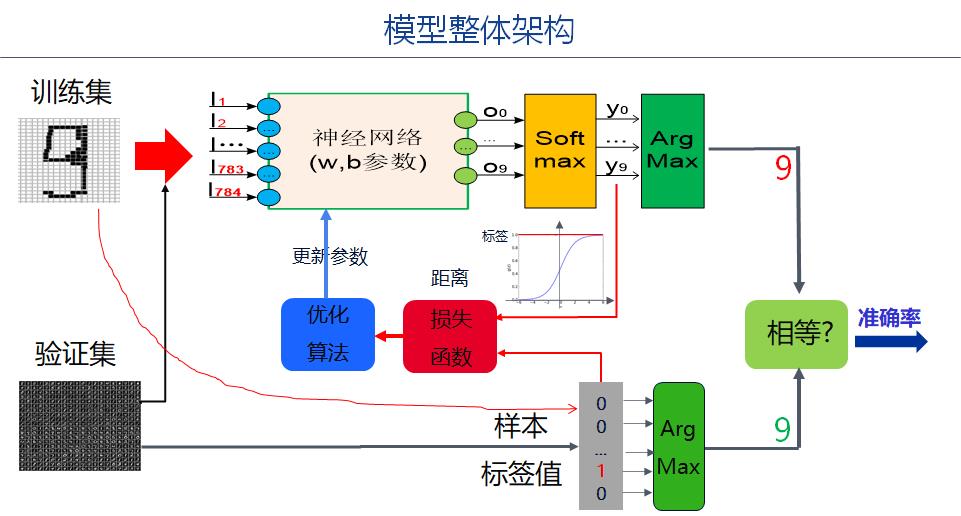
2.2 绝对值误差法(原始误差)
预测值与输出值之间的距离最直接的方法就是:用标签值与预测值相减。
- 当Yi标签为1时:loss = (1 - Yi_pred) = 1 - Yi_pred = 1 - x ; x在[0, 1]
- 当Yi标签为0时:loss = (Yi_pred - 0) = Yi_pred = x ; x在[0, 1]
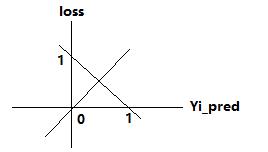
这种方法并没有对(Yi-Yi_pred)进行放大,只是线性运算
这种方法的loss函数有最小值
这种方法的loss函数的导数恒定为1
2.3 均方差法(平方误差)
- 当Yi标签为1时:loss = (1 - Yi_pred)^2 = (1 - x)^2 ; x在[0, 1]
- 当Yi标签为0时:loss = (Yi_pred - 0)^2 = (x^2 ; x在[0, 1]
这种方法对(Yi-Yi_pred)进平方放大。是一个凸函数
这种方法的loss函数有最小值
这种方法的loss函数的导数不恒定。
但该函数,应有于逻辑分类时,最大的问题是:loss函数有大量的局部最小值。
2.4 log误差
(1)log函数的几何图形
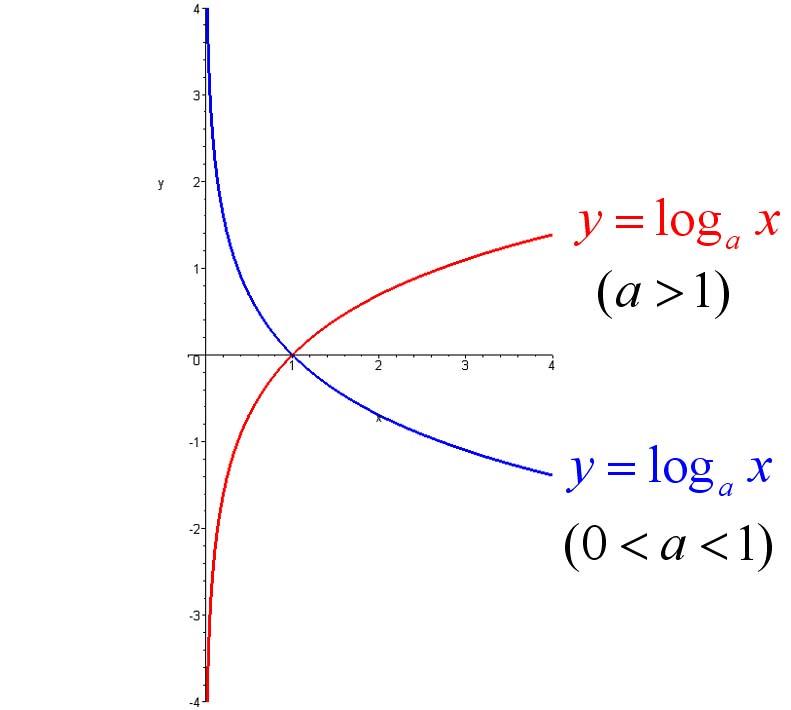
有图像可以看出:当大于1时:
- 在【-无穷,0】区间: 无映射
- 在【0,1】映射区间: 映射具有放大作用,即【0,1】映射到【-无穷,0】
- 在【1, +无穷】区间:映射具有缩小作用,即【1, +无穷】映射到【0, +无穷】
log损失函数,主要利用的是log函数在【0,1】区间的放大作用。
(2)不能直接利用log
- 当Yi标签为1时:loss = log(1 - Yi_pred) = log(1-x)
当Yi_pred接近标签1时,loss接近于log(1-1)=log0=负无穷, 而不是接近于0,很显然,这与loss的定义正好相反。
当Yi_pred接近于离标签1最远的0时,loss接近于log(1-)=log1=0,而不是接近于无穷大,很显然,这与loss的定义正好相反。
- 当Yi标签为0时:loss = log(Yi_pred - 0) = log(x)
当Yi_pred接近标签0时,loss接近于log(0)=log0=负无穷, 而不是接近于0,很显然,这与loss的定义正好相反。
当Yi_pred接近于离标签0最远的1时,loss接近于log(1) = 0,而不是接近于无穷大,很显然,这与loss的定义正好相反。
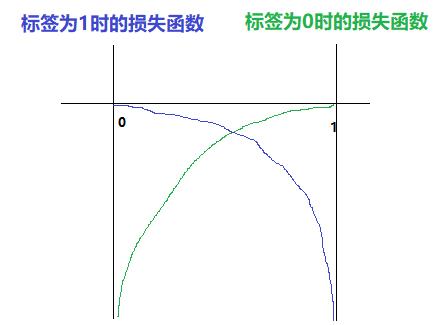
(2)第一次改造后的log损失函数
- 当Yi标签为1时:loss = log(Yi_pred) = log(x)
当Yi_pred接近于离标签1最近的1时,loss接近于log(1) = 0, 很显然,与损失函数的定义是一致的。
当Yi_pred接近于离标签1最远的0时,loss接近于log(0) = 负无穷,很显然,与损失函数相一致,但此时,如果loss接近于“正”无穷就更好了 。
- 当Yi标签为0时:loss = log(1- Yi_pred) = log(1-x)
当Yi_pred接近于离标签0最近的0时,loss接近于log(1-0) = 0, 很显然,与损失函数的定义是一致的。
当Yi_pred接近于离标签1最远的1时,loss接近于log(1-1) = 负无穷,很显然,与损失函数相一致,但此时,如果loss接近于“正”无穷就更好了 。
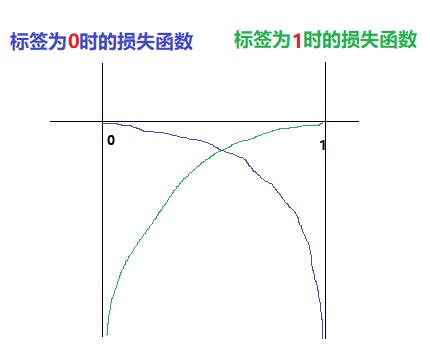
(3)第二次改造后的log损失函数
- 当Yi标签为1时:loss = -log(Yi_pred) = -log(x)
当Yi_pred接近于离标签1最近的1时,loss接近于log(1) = 0, 很显然,与损失函数的定义完全一致。
当Yi_pred接近于离标签1最远的0时,loss接近于log(0) = 正无穷,很显然,与损失函数的定义完全一致
- 当Yi标签为0时:loss = -log(1- Yi_pred) = -log(1-x)
当Yi_pred接近于离标签0最近的0时,loss接近于log(1-0) = 0, 很显然,与损失函数的定义完全一致。
当Yi_pred接近于离标签1最远的1时,loss接近于log(1-1) = 正无穷,很显然,与损失函数的定义完全一致。
第3章 0-1 损失函数: 0-1
3.1 数学表达式

在上图中:|Y-F(x)| = |Yi - Yi_pred|, 表示样本标签值与预测值的实际距离。
3.2 几何图形
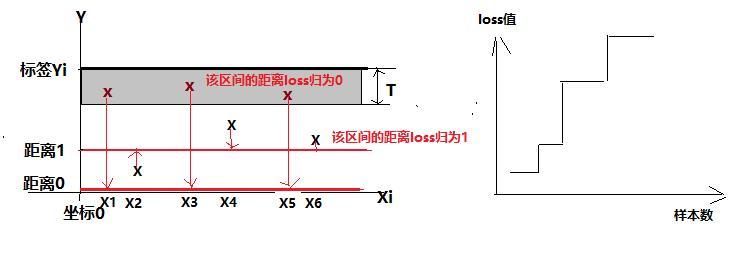
在上图中,T为门限超参数,所有落在区间T内的样本点,都认为与标签Yi是一致的,因此loss都归为0,所有区间外的样本点,都认为与标签Yi是不一致的,因此loss都归为1。
Yi_pred的输出值在[0,1]之间,这种loss函数对所有样本点loss值的累计和,不是连续的,而是阶梯式的 ,离散的,粒度为1.
第4章 交叉熵函数:二分类
4.1 交叉熵与二分类
交叉熵主要用于sigmoid实现二分类预测的损失函数。
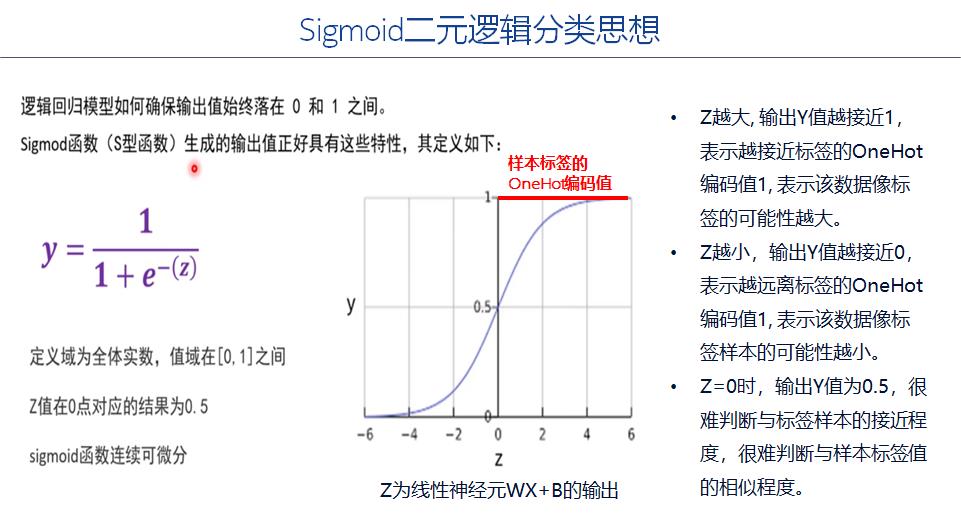
二分类预测的特点是:
- 预测输出值在【0,1】区间。
- 样本的标签只有两种:0或1
4.2 交叉熵概述
交叉熵(Cross Entropy)是Shannon信息论中一个重要概念,主要用于度量两个概率分布间的差异性信息。
在信息论中,交叉熵是表示两个概率分布p,q,其中p表示真实分布,q表示非真实分布,在相同的一组事件中,其中,用非真实分布q来表示某个事件发生所需要的平均比特数。从这个定义中,我们很难理解交叉熵的定义。下面举个例子来描述一下:
假设现在有一个样本集中两个概率分布p,q,其中p为真实分布,q为非真实分布。
假如,按照真实分布p来衡量识别一个样本所需要的编码长度的期望为:


4.3 交叉熵损失函数概述
交叉熵损失函数只是利用了交叉熵函数的数学形式,但含义却完全不同。
因此,我们并不打算从概率论和信息论的角度来解读交叉上损失函数的意义,而是从损失函数自身的定义来解读该损失函数。
损失函数的本质是描述预测值与标签值之间的距离或差异性大小的函数,因此我们从这个角度来参数。
交叉熵损失函数本质上是log损失函数!!!
4.4 交叉熵损失函数形式(根据标签不同而不同)
交叉熵损失函数针对二分类而引入的损失函数,二分类有两个标签:1或0,因此,其函数形式也有两个。
与信息论交叉熵函数的关系:
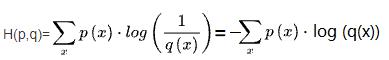
(1)当Yi标签为1时:loss = -log(Yi_pred) = -log(x)
损失函数的意义:
- 当Yi_pred接近于离标签1最近的1时,loss接近于log(1) = 0,
- 当Yi_pred接近于离标签1最远的0时,loss接近于log(0) = 正无穷。
信息量交叉熵的含义:
- 令样本标签1代表p(x)概率; 输出Yi_pred代表概率q(x)
(2)当Yi标签为0时:loss = -log(1- Yi_pred) = -log(1-x)
损失函数的意义:
- 当Yi_pred接近于离标签0最近的0时,loss接近于log(1-0) = 0, 很显然,与损失函数的定义完全一致。
- 当Yi_pred接近于离标签1最远的1时,loss接近于log(1-1) = 正无穷,很显然,与损失函数的定义完全一致。
信息量交叉熵的含义:
- 令样本标签0代表p(x)概率=1 - p(x); 输出Yi_pred代表概率 1- q(x)
(3)汇总后统一的函数的形式

这里N是指样本的数量。
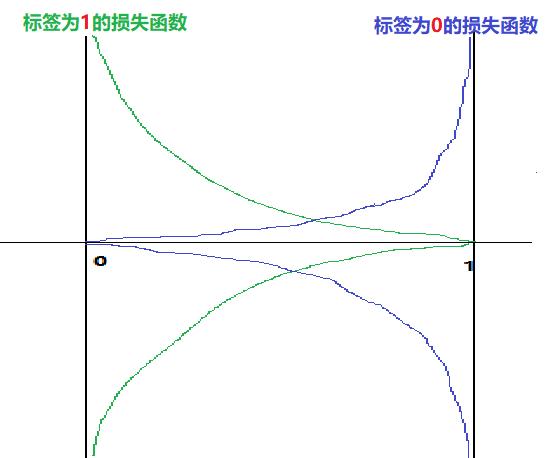
4.5 交叉上损失函数的几何图形
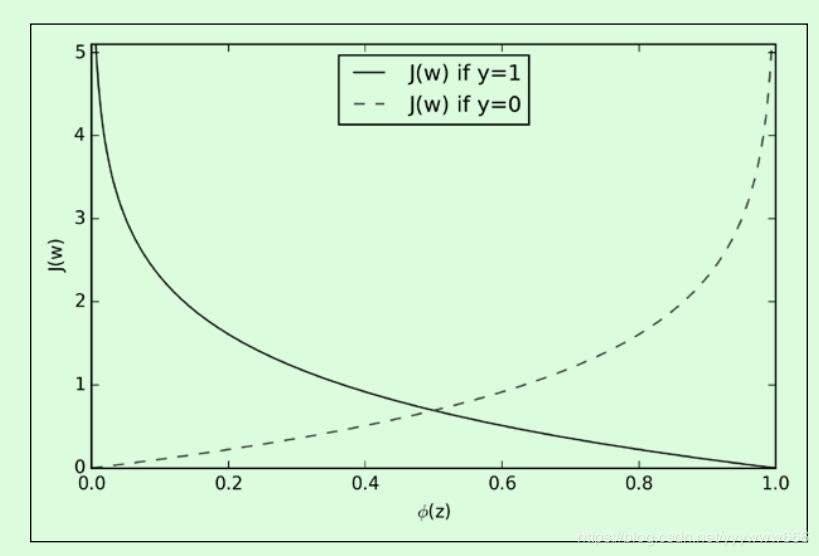
(1)实线是OneHot编码中,标签值“1”出的损失函数。
- 当x趋近与1时,y趋近于0
- 当x趋近与0时,y趋近于+无穷
(2)实线是OneHot编码中,标签值“0”处的损失函数。
- 当x趋近与1时,y趋近于+无穷
- 当x趋近与0时,y趋近于0
第5章 交叉熵函数:多分类
5.1 函数形式

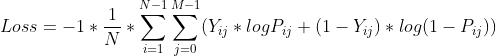
其中:
N是样本数,i是样本索引。
M是分类数,j是分类索引。
Pij是第i个样本的第j路输出。
第6章 -log对数损失函数NLL:多分类
当(1)样本的标签Yi是0或1时,(2)且预测输出Yi_pred在0和1之间时,则,在多分类时,Yi_pred与标签的距离,可以直接用负对数来表示。
多分类是对二分类的拓展,
6.1 负对数损失函数的数学表达式
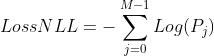
M是分类数,j是分类下标。
6.2 负对数损失函数的几何图形
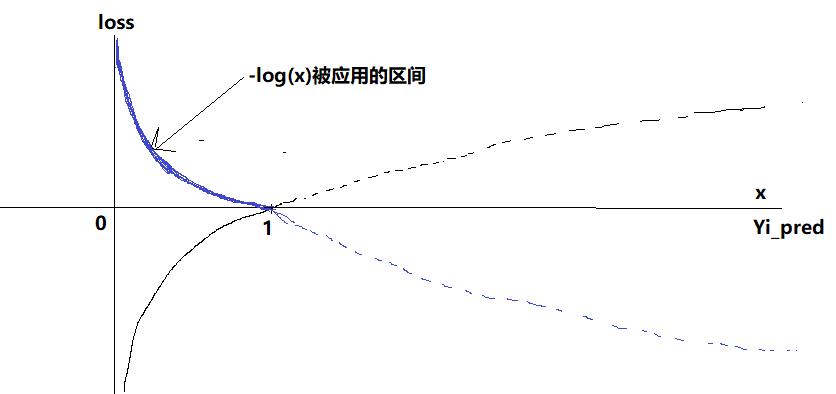
蓝色的图形是负对数函数,
x轴是sigmoid函数或softmax函数的输出,数值在[0,1]之间。
y轴是loss函数的输出值,区间为【0,+无穷】
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120559396
以上是关于[人工智能-深度学习-14]:神经网络基础 - 常见loss损失函数之逻辑分类,对数函数,交叉熵函数的主要内容,如果未能解决你的问题,请参考以下文章