GMM高斯混合模型
Posted 好奇小圈
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了GMM高斯混合模型相关的知识,希望对你有一定的参考价值。
文章目录
前言
阅读背景差分算法相关文献碰到了这个模型,比较生疏,故此学习。
一、模型介绍
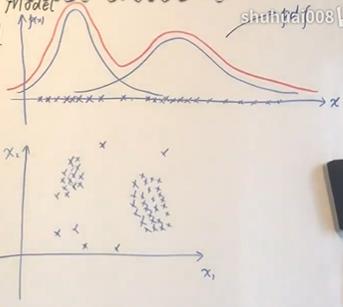
如图所示,横轴上的数据集的密度函数可以视为两个高斯分布的叠加。
从几何角度看,可以将其视为多个高斯分布叠加的加权平均。
p
(
x
)
=
∑
k
=
1
K
α
k
N
(
x
∣
μ
k
,
∑
k
)
,
∑
k
=
1
K
α
k
=
1
p(x)=\\sum_k=1^K \\alpha_k N(x |\\mu_k,\\sum_k ),\\sum_k=1^K \\alpha_k=1
p(x)=k=1∑KαkN(x∣μk,∑k),k=1∑Kαk=1
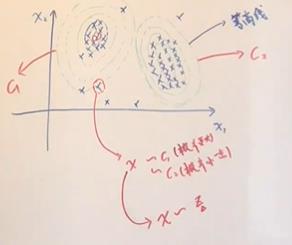
从混合模型(生成模型)角度来看,x(observed variable),z(latent variable->对应的样本x属于哪一个高斯分布->离散随机变量)
如下表所示
| z | c 1 c_1 c1 | c 2 c_2 c2 | … | c k c_k ck |
|---|---|---|---|---|
| p(x) | p 1 p_1 p1 | p 2 p_2 p2 | … | p k p_k pk |
概率图表示:
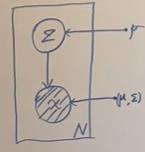
其中p=
p
1
,
p
2
,
.
.
.
,
p
k
p_1,p_2,...,p_k
p1,p2,...,pk
二、极大似然
将p(x)分解:
p
(
x
)
=
∑
z
p
(
x
,
z
)
=
∑
k
=
1
K
p
(
x
,
z
=
c
k
)
=
∑
k
=
1
K
p
(
z
=
c
k
)
⋅
p
(
x
∣
z
=
c
k
)
=
∑
k
=
1
K
p
k
⋅
N
(
x
∣
μ
k
,
∑
k
)
p(x)=\\sum_z p(x,z) \\\\=\\sum_k=1^K p(x,z=c_k) \\\\=\\sum_k=1^K p(z=c_k)\\cdot p(x|z=c_k) \\\\=\\sum_k=1^K p_k \\cdot N(x|\\mu_k,\\sum_k)
p(x)=z∑p(x,z)=k=1∑Kp(x,z=ck)=k=1∑Kp(z=ck)⋅p(x∣z=ck)=k=1∑Kpk⋅N(x∣μk,∑k)
一些参数:
X:observed data->X=(
x
1
,
x
2
,
.
.
.
,
x
N
x_1,x_2,...,x_N
x1,x2,...,xN)
(X,Z):complete data
θ \\theta θ:parameter-> θ = p 1 , p 2 , . . . , p k , μ 1 , μ 2 , . . . , μ k , ∑ 1 , ∑ 2 , . . . , ∑ k \\theta=\\p_1,p_2,...,p_k,\\mu_1,\\mu_2,...,\\mu_k,\\sum_1,\\sum_2,...,\\sum_k \\ θ=p1,p2,...,pk,μ1,μ2,...,μk,∑1,∑2,...,∑k
θ ^ = a r g m a x θ log ( p ( x ) ) = a r g m a x θ log ( ∏ i = 1 N p ( x ) ) = a r g m a x θ ∑ i = 1 N log ( p ( x ) ) = a r g m a x θ ∑ i = 1 N log ( ∑ k = 1 K p k ∼ N ( x ∣ μ k , ∑ k ) ) \\hat\\theta=arg max_\\theta \\log(p(x)) \\\\=arg max_\\theta \\log(\\prod_i=1^N p(x)) \\\\=arg max_\\theta \\sum_i=1^N \\log(p(x)) \\\\=arg max_\\theta \\sum_i=1^N \\log(\\sum_k=1^K p_k \\thicksim N(x|\\mu_k,\\sum_k)) θ^=argmaxθlog(p(x))=argmaxθlog(∏i=1Np(x))=argmaxθ∑i=1Nlog(p(x))=argmaxθ∑i=1Nlog(∑k=1Kpk∼N(x∣μk,∑k))
三、EM求解
EM公式: θ t + 1 = a r g m a x E z ∣ x , θ t [ log p ( x , z ∣ θ ) ] \\theta^t+1=argmax E_z|x,\\theta^t[\\log p(x,z|\\theta)] θt+1=argmaxEz∣x,θ