集成学习-装袋法和提升法

Posted 2022-04-22 文藏藏

• 集成学习(ensemble learning)是时下非常流行的机器学习算法，它本身不是一个单独的机器学习算法，而是通 过在数据上构建多个模型，集成所有模型的建模结果。

目录

前言

一、集成学习是什么？

二、装袋法Bagging

 1.随机森林-代表集成学习技术水平的算法（有放回的抽样bagging）

1.1 简介

1.2 什么是随机

1.3  优秀之处

1.4 唯一缺点 

1.5 拥有森林（如何构建随机森林）

1.6 sklearn建立森林

1.7 分类实例（基于红酒数据集）

1.8 oob_score_（红酒集）

1.9 回归实例（基于乳腺癌预测模型）

 2.0 调参

总结

---

前言

例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。

一、集成学习是什么？

集成学习本身不是一个单独的机器学习算法，而是通过再数据上构建多个模型，集成所有模型的建模结果。

目标：集成学习算法本身是考虑多个建模器的建模结果，汇总得到一个综合的结果，总的来说就是比单个模型获得更好的分类和回归效果表现。或者说在机器学习的众多算法中，我们的目标是学习出一个稳定的且在各个方面表现都较好的模型，但实际情况往往不这么理想，有时我们只能得到多个有偏好的模型（弱监督模型（弱评估器，基评估器），在某些方面表现的比较好）。集成学习就是组合这里的多个弱监督模型一起得到一个更好更全面的强监督模型。

通俗理解：有一道判断题，一群学习不好的人怎么去做能让题目的成功率比较高呢。

在这里就有两种方法：

第一种是序列集成方法（提升法Boosting）：

先让学渣A做一遍，然后再让学渣B做，且让B重点关注A做错的那些题，再让C做，同样重点关注B做错的，依次循环，直到所有的学渣都把题目做了一遍为止

第二种就是并行集成方法（装袋法Bagging）：

多个学渣一起做， 每个人随机挑选一部分题目来做，最后将所有人的结果进行汇总，然后根据将票多者作为最后的结果

图：

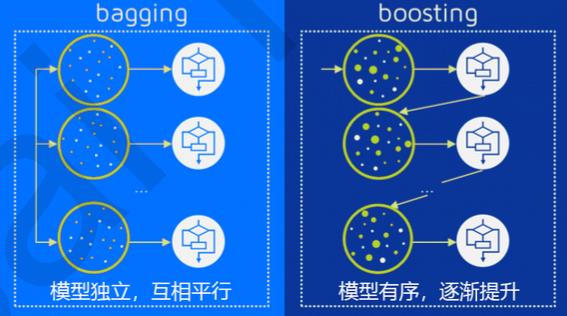
二、装袋法Bagging

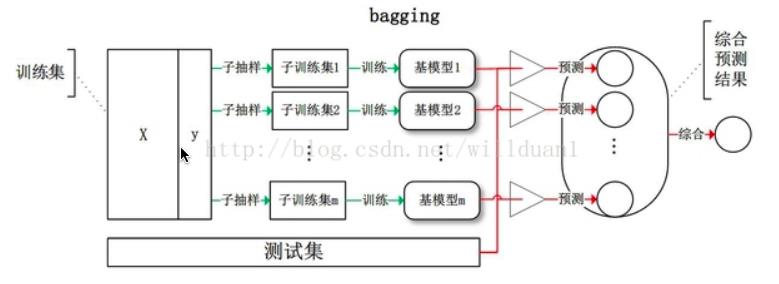
 全称为bootstrap aggregating。它是一种有放回的抽样方法，其算法过程如下：
        - 从原始样本集中抽取训练集。每轮从原始样本集中使用有放回的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）
        - 每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）
        - 对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

 1.随机森林-代表集成学习技术水平的算法（有放回的抽样bagging）

1.1 简介

        随机森林是一种有监督学习算法，是以CART决策树为基学习器的集成学习算法。随机森林非常简单，易于实现，计算开销也很小，在分类和回归上表现出非常惊人的性能，因此，随机森林被誉为“代表集成学习技术水平的方法”。

1.2 什么是随机

数据集的随机选择：从原始数据集中采取《有放回的抽样bagging》，构造子数据集，子数据集的数据量是和原始数据集相同的。不同子数据集的元素可以重复，同一个子数据集中的元素也可以重复

待选特征的随机选取：随机森林中的子树的每一个分裂过程并未用到所有的待选特征，而是从所有的待选特征中随机选取一定的特征，之后再随机选取的特征中选取最优的特征。

1.3  优秀之处

• 可以用于分类问题，也可以用于回归问题
• 可以解决模型过拟合的问题，对于随机森林来说，如果随机森林中的树足够多，那么分类器就不会出现过拟合
• 可以检测出特征的重要性，从而选取好的特征
• 由于采用了集成算法，本身精度比大多数单个算法要好，所以准确性高
• 由于两个随机性的引入，使得随机森林不容易陷入过拟合（样本随机，特征随机）
• 在工业上，由于两个随机性的引入，使得随机森林具有一定的抗噪声能力，对比其他算法具有一定优势
• 它能够处理很高维度（feature很多）的数据，并且不用做特征选择，对数据集的适应能力强：既能处理离散型数据，也能处理连续型数据
• 在训练过程中，能够检测到feature间的互相影响，且可以得出feature的重要性，具有一定参考意义

1.4 唯一缺点 

        当随机森林中的决策树个数很多时，训练时需要的空间和时间会比较大

1.5 拥有森林（如何构建随机森林）

• 从原始训练集中随机有放回采样取出m个样本,生成m个训练集
• 对m个训练集，我们分别训练m个决策树模型
• 对于单个决策树模型，假设训练样本特征的个数为n，那么每次分裂时根据信息增益/信息增益比/基尼指数 选择最好的特征进行分裂
• 将生成的多颗决策树组成随机森林。对于分类问题，按照多棵树分类器投票决定最终分类结果；对于回归问题，由多颗树预测值的均值决定最终预测结果

1.6 sklearn建立森林

建立森林的时候会有分类和预测两种实现（sklearn.ensemble）

    - RandomForestClassifier  分类
    - RandomForestRegression  回归

1.7 分类实例（基于红酒数据集）

• 库的引入

from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split,cross_val_score
from sklearn.model_selection import 
import matplotlib.pyplot as plt
%matplotlib inline

•  模型的构建

wine = load_wine()
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
clf = DecisionTreeClassifier(random_state=0)
rfc = RandomForestClassifier(random_state=0)
clf = clf.fit(Xtrain,Ytrain)
rfc = rfc.fit(Xtrain,Ytrain)
score_c = clf.score(Xtest,Ytest)
score_r = rfc.score(Xtest,Ytest)
print(score_c,score_r)

在这里得到

决策树的得分：0.9259259259259259

随机森林的得分：0.9814814814814815

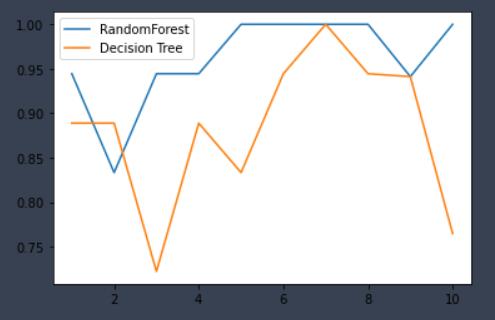
• 画出随机森林和决策树在十折交叉验证下的对比折线图

rfc = RandomForestClassifier(n_estimators=25)
rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10)
clf = DecisionTreeClassifier()
clf_s = cross_val_score(clf,wine.data,wine.target,cv=10)
plt.plot(range(1,11),rfc_s,label = "RandomForest")
plt.plot(range(1,11),clf_s,label = "Decision Tree")
plt.legend()
plt.show()

十折交叉验证：将数据集分成十份，轮流将其中9份作为训练数据，1份作为测试数据，进行试验。

• 画出随机森林和决策树在十组十折交叉验证下得到的折线图

rfc_l = []
clf_l = []
for i in range(10):
    rfc = RandomForestClassifier(n_estimators=25)
    rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    rfc_l.append(rfc_s)
    clf = DecisionTreeClassifier()
    clf_s = cross_val_score(clf,wine.data,wine.target,cv=10).mean()
    clf_l.append(clf_s)
plt.plot(range(1,11),rfc_l,label = "Random Forest")
plt.plot(range(1,11),clf_l,label = "Decision Tree")
plt.legend()
plt.show()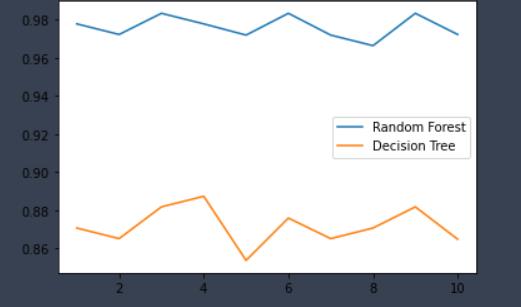

以上可以看出在不考虑时间空间的影响下随机森林的效果优于决策树算法。

1.8 oob_score_（红酒集）

随机森林的又放回抽样也有一些问题，由于是有放回，一些样本可能会被采集多次，而其他一些样本却可能被忽略，一次都未被采集到。那么这些被忽略或者一次都没被采集到的样本叫做oob袋外数据。因此我们可以采用一种不同划分测试集和训练集，相当于将袋外数据作为测试集，这样只需要将RandomForestClassifier（oob_score=True）设置为True,就可以查看oob_score_的成绩了。

以下是基于红酒集的代码实现

rfc = RandomForestClassifier(n_estimators=25,oob_score=True)
rfc = rfc.fit(wine.data,wine.target)
#重要属性oob_score_ 
rfc.oob_score_
 

1.9 回归实例（基于乳腺癌预测模型）

• 库的导入

from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split,cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
%matplotlib inline

• 模型的训练

data = load_breast_cancer()
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
rfr = RandomForestRegressor()
LR = LinearRegression()
rfr.fit(Xtrain,Ytrain)
R.fit(Xtrain,Ytrain)
rfr.score(Xtest,Ytest)
LR.score(Xtest,Ytest)

训练成绩为

随机森林 0.9446334928229665

线性回归 0.8944412211446326

• 十折交叉验证下的对比

rfr_s = cross_val_score(rfr,data.data,data.target,cv=10)
LR_s = cross_val_score(LR,data.data,data.target,cv=10)
plt.plot(range(1,11),rfr_s,label = "RandomForest")
plt.plot(range(1,11),LR_s,label = "linearRegression")
plt.legend()
plt.show()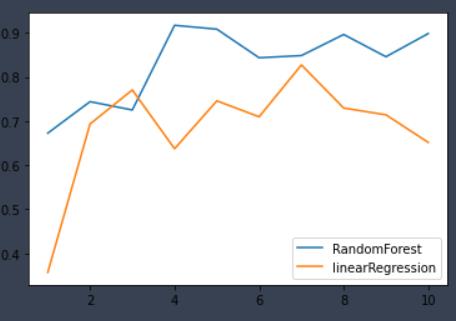

 2.0 调参

由以上两个实例可以看出集成算法中装袋法代表随机森林明显优于传统的回归模型和分类模型，影响随机森林重要的一部分还有参数的设置，下面基于网格搜索对于随机森林进行调参。

• 控制弱评估器的参数

调参顺序

• n_estimators : 最重要的参数，控制生成的树木数量，调至平稳就可以
• max_features（最大特征数）:有增有减，默认最大深度，即最高复杂度，向复杂度降低的方向调参max depth越小，模型更简单，且向图像的左边移动
• min samples leaft：有增有减，默认最小限制1，即最高复杂度，向复杂度降低的方向调参，min samples leaft越大模型更简单，且向图像的左边移动
• min samples split：有增有减，默认最小限制2，即最高复杂度，向复杂度降低的方向调参，min samples split越大模型更简单，且向图像的左边移动
• max features：一般设置为’auto'
• criterion: 一般采用’gini‘

---

总结

本文着重说明了集成学习的两种方法的区别，以及装袋法的代表算法随机森林的原理以及调参技巧等。