数字信号处理相关函数应用 ( 正弦信号 的 自相关函数 分析 | 在白噪声中检测正弦信号 )

Posted 2022-03-05 韩曙亮

文章目录

• 一、正弦信号 的 自相关函数 分析

一、正弦信号 的 自相关函数 分析

---

正弦信号 $A\sin \omega n$ ,

其 幅度 $A=1$ , 功率 $P_s=0.5$ , 下图是该正弦信号的函数图 :

白噪声信号 $N(n)$ , 方差 $1$ , 信噪比 $\mathrm{S}\mathrm{N}\mathrm{R}=-3\mathrm{d}\mathrm{B}$ , 信号长度为 $512$ ;

下图是 正弦信号 $s(n)=A\sin \omega n$ 与 白噪声信号 $N(n)$ 叠加后的 函数图 :

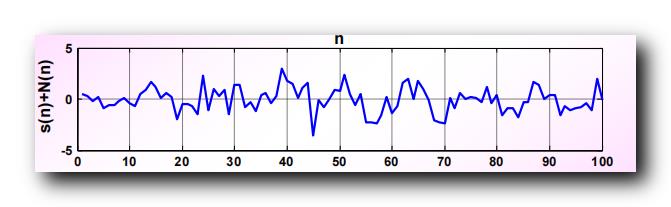
从上图中 , 基本看不到信号 , 信号完全淹没在噪声中了 ;

求 正弦信号 $s(n)=A\sin \omega n$ 与 白噪声信号 $N(n)$ 叠加后 的信号的 相关函数 $r(m)$ , 可以得到如下的函数图 :

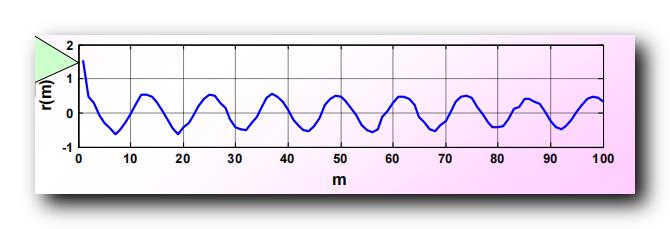
在 自相关函数 $r(m)$ 中的 $m=0$ 点处 , 相关性很大 , 此处是
$$信号功率+噪声功率=1.5$$

信号功率是 $0.5$ , 噪声的功率是 $1$ ,

在 $m=0$ 处 , 白噪声的功率是 $1$ , 信号的功率是 $0.5$ ;

在其它地方 $m\ne 0$ 时 , 白噪声功率趋近于 $0$ , 只剩下 信号功率了 , 这样实现了在 噪声中 检测 信号 ;