学习理论有什么用？

Posted 2022-02-07 卓晴

简 介： 现在很多功能强大的软件使得我们分析数据的效率大大提高。虽然我们依靠软件来处理数据，但对计算结果的应用却不能完全依赖软件，还需要对其背后的原理有着清晰的理解，这样才能够正确揭示出数据背后的物理原理。本文对于FFT分析谐波信号频谱所出现的“栅栏现象”的背后的原理进行的分析。

关键词： FFT，栅栏现象，频率泄露

 

§01 问题提出

---

  卓老师，请教个问题，我定义了几个幅值都是1的不同频率的复指数信号的和的函数y，可为啥y的fft的结果，它们的幅值不一样呢？卓大大，拜请解答下，不胜感激。

▲ 图1.1 求信号FFT的MATLAB程序

  上面的MATLAB中的定义的信号如下：

$$y\left(t\right)=e^{j2\pi 5t}+e^{j2\pi 10t}+e^{j2\pi 30t}+e^{j2\pi 40t},t=n\cdot T_s$$

  利用FFT计算出频谱数值，取结果的模块绘制如下：

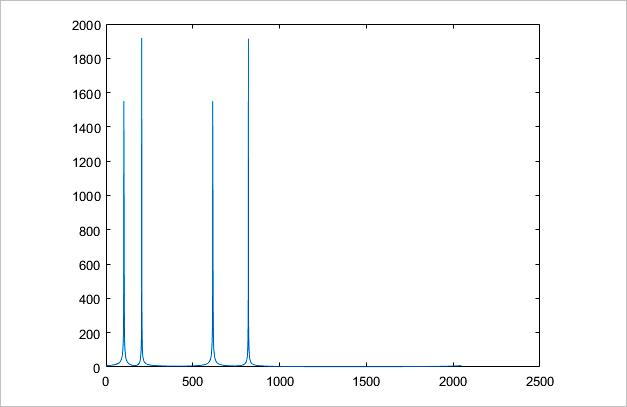
▲ 图1.2 数据FFT的幅度谱

  定义了几个幅值都是1的不同频率的复指数信号的和的函数y，可为啥y的fft的结果，它们的幅值不一样呢？

  目前猜测可能有两个原因：
  1. 栅栏效应；
  2. 因为N取得点数不是周期的整数倍，所以导致周期延拓后其实就不是一个标准正弦信号。

 

§02 FFT变换结果

---

  首先，你利用FFT求取的信号是复震荡信号，所以求出的FFT（信号的离散频谱）结果中对应每个频率出现是一个频率尖峰。整体上你所得到的结果反映了信号中频率分布的情况。

2.1 问题分析

  你的疑问反映了FFT的结果与信号实际频谱之间存在着某些差异。为了突出你的问题，可以看到如下所显示的5Hz与10Hz两个信号的变化。这是在原有信号频率（5Hz，10Hz）的基础上，增加了一个微小的频率变化：

$$f_5=5+\Delta f,f_{20}=20+\Delta f$$

  其中：$\Delta f\in \left(0,0.05\right)$。

  从图中可以看到频谱出现了两种变化：

• FFT计算结果中的频谱的幅度在上下变化；
• 在单个频谱谱线周围还有一些小的频谱的分布，而且随着频谱幅值变化，这些小频谱的大小也发生变化。

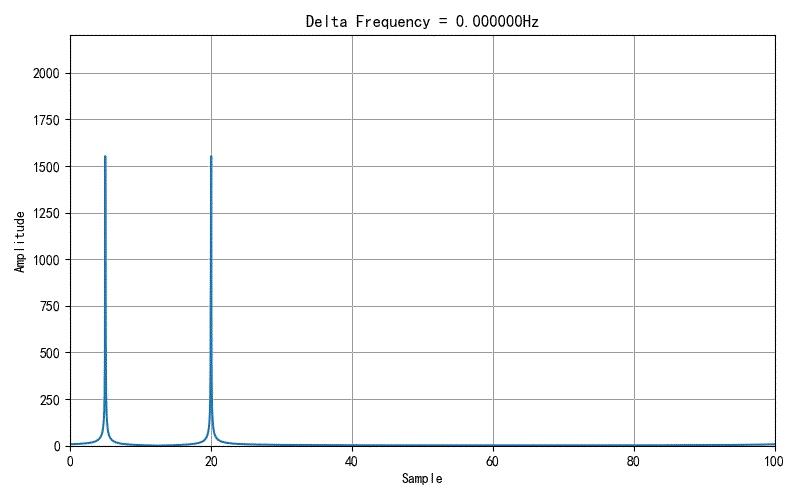
▲ 图 不同的频率偏移下谱线高度变化

  由于在上述绘制FFT结果是，使用的连线绘制方式。如果使用离散数据线（火柴杆）绘制离散频谱，就可以清楚知道结果数值的变化情况。

  下面是显示的在20Hz周围FFT结果幅值的变化。可以看到FFT结果中，在20Hz周围实际上包含着大大小小多个频谱，随着信号中频谱的微小增加，频谱谱线出现高低变化。特别是在特殊的频谱时计算结果中就只剩下一个频谱，此时它的幅值最高，20Hz周期其他离散频谱都消失了。

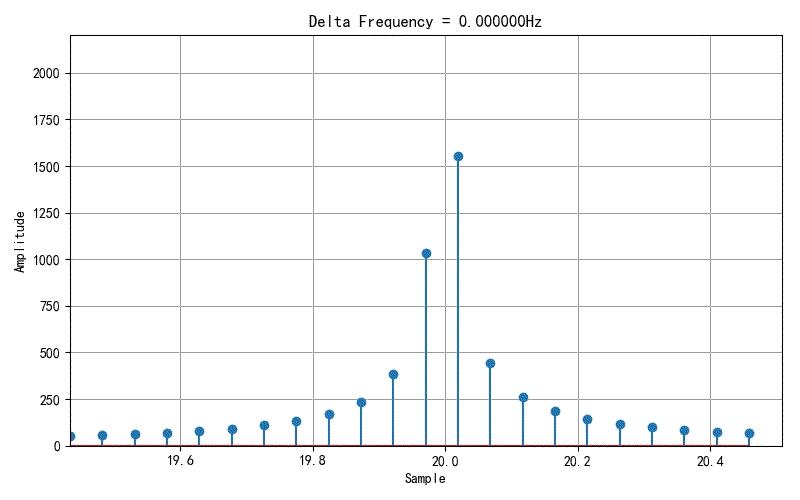
▲ 在20Hz 附近的谱线变化情况

  在最终解释之前，看一下下面的动图，你会发现FFT计算出的数值实际上是在一个连续的sinc信号（sinc信号的绝对值）上进行采样。随着sinc信号的中心点逐步增加，对应的FFT采样的离散频谱的幅度就会发生比较大的变化。

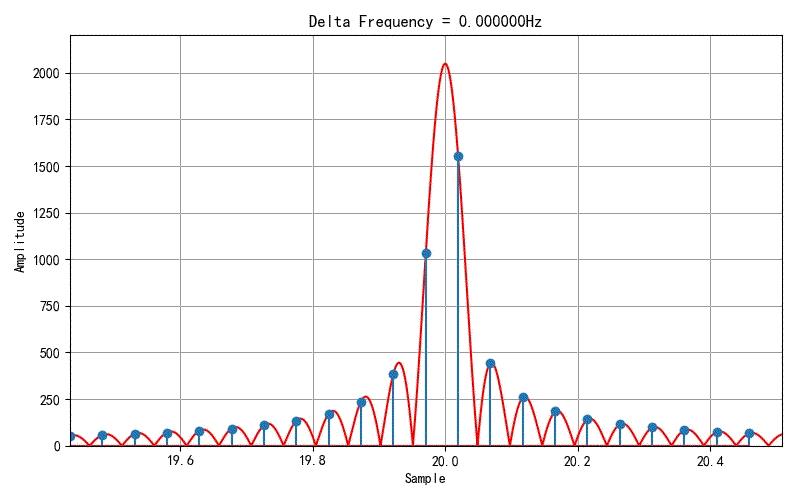
▲ 图 增加了连续频谱后的图像

  如果理解了FFT结果的这种特性，也就不难理解，为什么对于相同的幅值，但不同的频率为什么FFT计算出频谱峰值高度不同了。那就是因为FFT对应的离散频谱点正好处在sinc函数的不同位置，造成采样结果与sinc函数的峰值之间出现偏差。

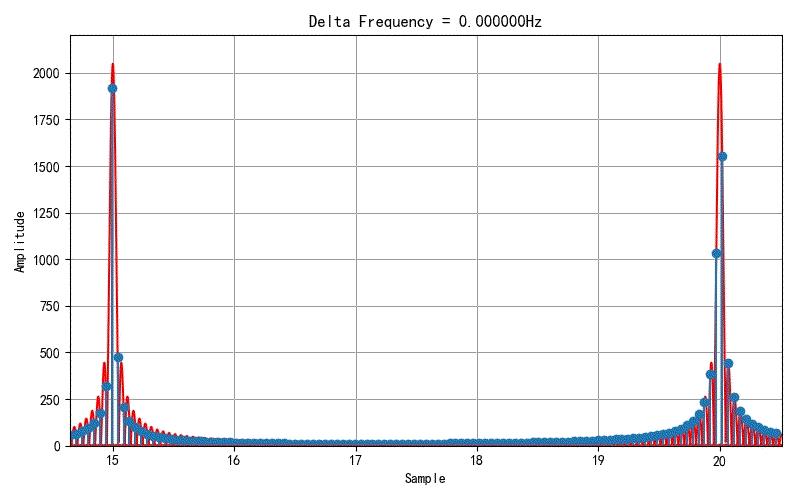
▲ 图 对比15Hz，20Hz两个频谱附近的变化

  只有当sinc函数的中心位置恰好与FFT离散频谱对齐是，此时对应FFT结果峰值最高，且周围也没有其他小的频谱分布了。

2.2 都是截断惹的祸

  使用FFT来分析信号的频谱实际上经过了以下四个步骤：

• 将原来的信号进行截断，形成离散时间信号；
• 将截断的信号进行采样，形成有限长离散时间信号；
• 将有限长离散信号进行周期延拓，形成周期离散序列。这一步骤是隐含在FFT的公示来源中，并不需要实际进行周期延拓；
• 将离散序列的时间间隔$T_s$等效成1，相当于将原来的信号进行尺度变化。

  对信号进行截断，相当于将原来的信号与一个有限长的矩形时间窗口相乘。所以截断后的信号频谱就等于原来信号频谱与矩形信号频谱的卷积结果。

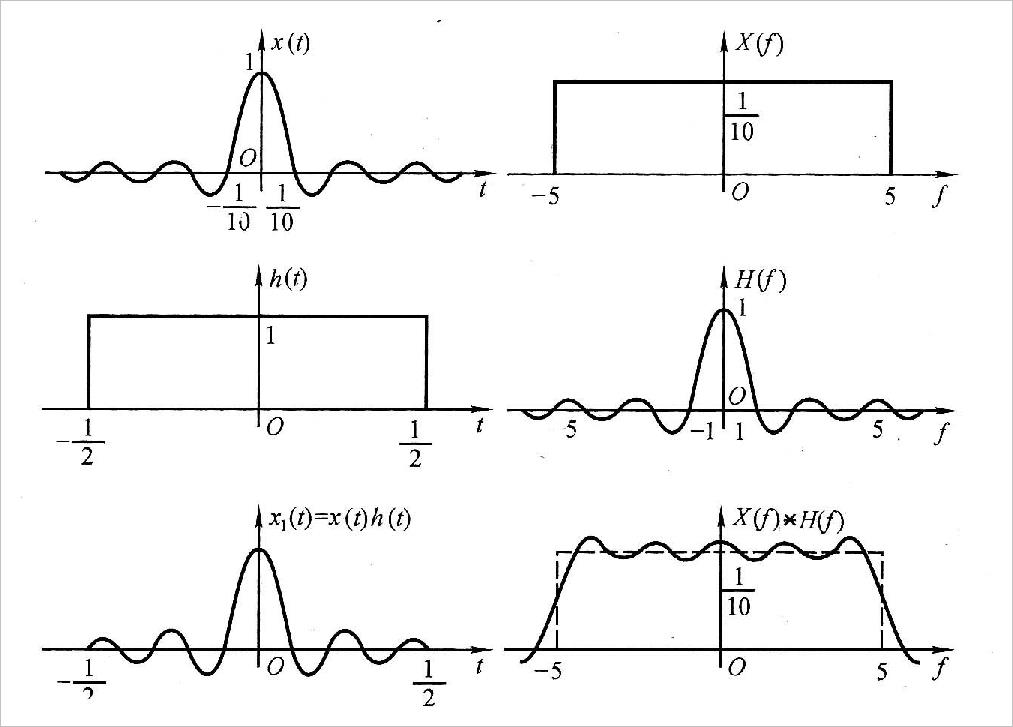
▲ 图2.2.1 信号由于被截断，它的频谱相当于被窗口信号频谱卷积

  因此上对应正弦震荡信号原本是冲激频谱信号，由于需要卷积举行时间窗口的频谱，所以对应的频谱就是一个sinc频谱了。在前面FFT采样中的sinc函数实际上就是对应信号截断时间窗口的傅里叶变换结果。

  对信号进行采样，得到离散序列信号的频谱时原来信号频谱的周期延拓，此时会产生频谱混叠现象。

  FFT的结果是对原始信号连续频谱的采样，也就是只能反映原来连续频谱在离散频率点初的取值，这种现象被称为“栅栏现象”。如果对应的信号频谱变换很大，栅栏现象就会造成频谱采样峰值变化很大。因此前面分析的现象可以看成栅栏现象的影响。

  对于FFT计算结果的幅值，需要考虑到$T_s$的影响，需要最终乘以$T_s$才能够真正反映出信号中频谱的幅值。

2.3 如何改善计算结果？

  通过上面分析，可以知道利用FFT来分析一些纯周期信号频谱的时候会出现较大的差异，如何避免上述截断、栅栏现象对于结果的影响呢？

2.3.1 信号能量

  如果仅仅通过信号的峰值来判断正弦信号频谱可能会出现较大的偏差，所以可以采用将峰值附近的频谱的能量累加起来，然后再计算机信号的峰值，这样可以避免因为栅栏现象所产生的峰值偏差；

  下图就是计算了20Hz附近20条频谱的能量对应的幅值随着频谱变化情况，可以看到对应的幅值变化不到1%。

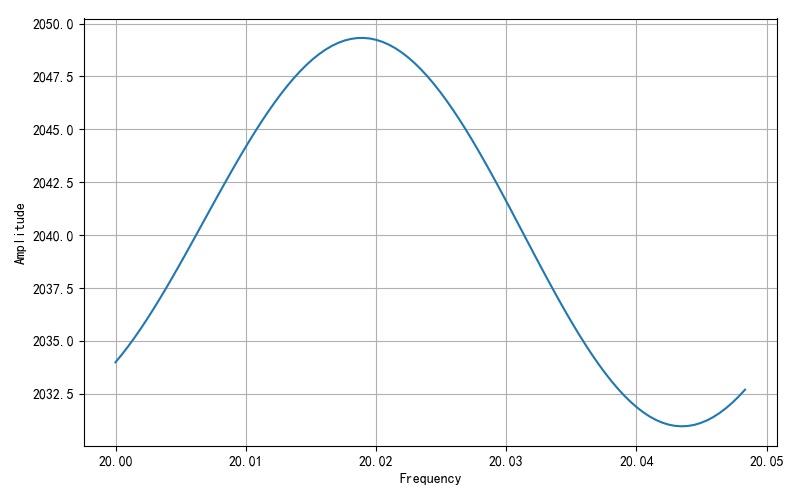
▲ 图2.3.1 20Hz附近频谱能量对应的幅值随着频谱变化情况

2.3.2 信号补零

  提高FFT结果频谱密度可以减少栅栏现象带来的偏差。在计算能力足够的情况下，通过增加截取信号的数据长度可以增加FFT结果频谱密度，即使简单在 原来采集数据的基础上，通过补零，来增加FFT计算数据的长度也可以有效增加FFT结果的频谱密度。

2.3.3 谐波估计

  如果已知信号中存在着少量不同频率的正弦信号，可以使用谐波估计处理方法，替代FFT，增强对正弦波幅度、频率、相位的估计精度。具体的算法参见现代信号处理相关的文档。

 

※ 总  结 ※

---

  现在很多功能强大的软件使得我们分析数据的效率大大提高。虽然我们依靠软件来处理数据，但对计算结果的应用却不能完全依赖软件，还需要对其背后的原理有着清晰的理解，这样才能够正确揭示出数据背后的物理原理。本文对于FFT分析谐波信号频谱所出现的“栅栏现象”的背后的原理进行的分析。

留言：我今天好像看到您了

▲ 图3.1 学生拍摄的照片

---

● 相关图表链接:

• 图1.1 求信号FFT的MATLAB程序
• 图1.2 数据FFT的幅度谱
• 图 不同的频率偏移下谱线高度变化
• 在20Hz 附近的谱线变化情况
• 图 增加了连续频谱后的图像
• 图 对比15Hz，20Hz两个频谱附近的变化
• 图2.2.1 信号由于被截断，它的频谱相当于被窗口信号频谱卷积
• 图2.3.1 20Hz附近频谱能量对应的幅值随着频谱变化情况

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST1.PY                     -- by Dr. ZhuoQing 2022-01-03
#
# Note:
#============================================================

from headm import *                 # =

fs = 100                            # Sample frequency
N = 2048                           # Data number
n = range(0,N)                      #
t = array(n)/fs

pltgif = PlotGIF()

deltafdim = []
energedim = []


for i in range(fs):
    deltaF = i/N
    y = exp(2*pi*(5+deltaF)*t*1.0j) + exp(1.0j*2*pi*t*(20+deltaF))

    x = fft.fft(y)
    m = abs(x)
    fdim = array(n)/(N/fs)

    startid = 390
    endid = 420

    ffdim = linspace(startid*fs/N, endid*fs/N, 5000)
    sincdim = abs(sinc((ffdim-(20+deltaF))*N/fs)*N)
    sincdim1 = abs(sinc((ffdim-(15+deltaF))*N/fs)*N)

    allenerge = sqrt(sum([s*s for s in m[startid:endid]]))
    energedim.append(allenerge)
    deltafdim.append(20+deltaF)



    #--------------------------------------------------------

    plt.clf()
    plt.figure(figsize=(8,5))
#    plt.plot(fdim, m)
    plt.plot(ffdim, sincdim, 'r')
    plt.plot(ffdim, sincdim1, 'r')
    plt.stem(fdim[startid:endid], m[startid:endid])
    plt.axis([startid*fs/N, endid*fs/N, 0, 2200])
    plt.title('Delta Frequency = %fHz'%deltaF)
    plt.xlabel("Sample")
    plt.ylabel("Amplitude")
    plt.grid(True)
    plt.tight_layout()
    plt.savefig(r"d:\\temp\\figure1.jpg")
    pltgif.append(plt)
    plt.close()
    tspshowimage(image=r"d:\\temp\\figure1.jpg")

    #--------------------------------------------------------

    break

#pltgif.save()

#------------------------------------------------------------
'''
plt.clf()
plt.figure(figsize=(8,5))
plt.plot(deltafdim, energedim)
plt.xlabel("Frequency")
plt.ylabel("Amplitude")
plt.grid(True)
plt.tight_layout()
plt.savefig(r"d:\\temp\\figure1.jpg")
plt.close()
tspshowimage(image=r"d:\\temp\\figure1.jpg")


print((max(energedim) - min(energedim)) / mean(energedim) * 100)

'''
#------------------------------------------------------------
#        END OF FILE : TEST1.PY
#============================================================