2023-02-14：魔物了占领若干据点，这些据点被若干条道路相连接， roads[i] = [x, y] 表示编号 xy 的两个据点通过一条道路连接。 现在勇者要将按照以下原则将这些据点逐一夺回：

Posted 2023-03-03 福大大架构师每日一题

2023-02-14：魔物了占领若干据点，这些据点被若干条道路相连接，
roads[i] = [x, y] 表示编号 x、y 的两个据点通过一条道路连接。
现在勇者要将按照以下原则将这些据点逐一夺回：
在开始的时候，勇者可以花费资源先夺回一些据点，
初始夺回第 j 个据点所需消耗的资源数量为 cost[j]
接下来，勇者在不消耗资源情况下，
每次可以夺回一个和「已夺回据点」相连接的魔物据点，
并对其进行夺回。
为了防止魔物暴动，勇者在每一次夺回据点后（包括花费资源夺回据点后），
需要保证剩余的所有魔物据点之间是相连通的（不经过「已夺回据点」）。
请返回勇者夺回所有据点需要消耗的最少资源数量。
输入保证初始所有据点都是连通的，且不存在重边和自环。
输入：cost = [1,2,3,4,5,6]，roads = [[0,1],[0,2],[1,3],[2,3],[1,2],[2,4],[2,5]]。
输出：6。

答案2023-02-24：

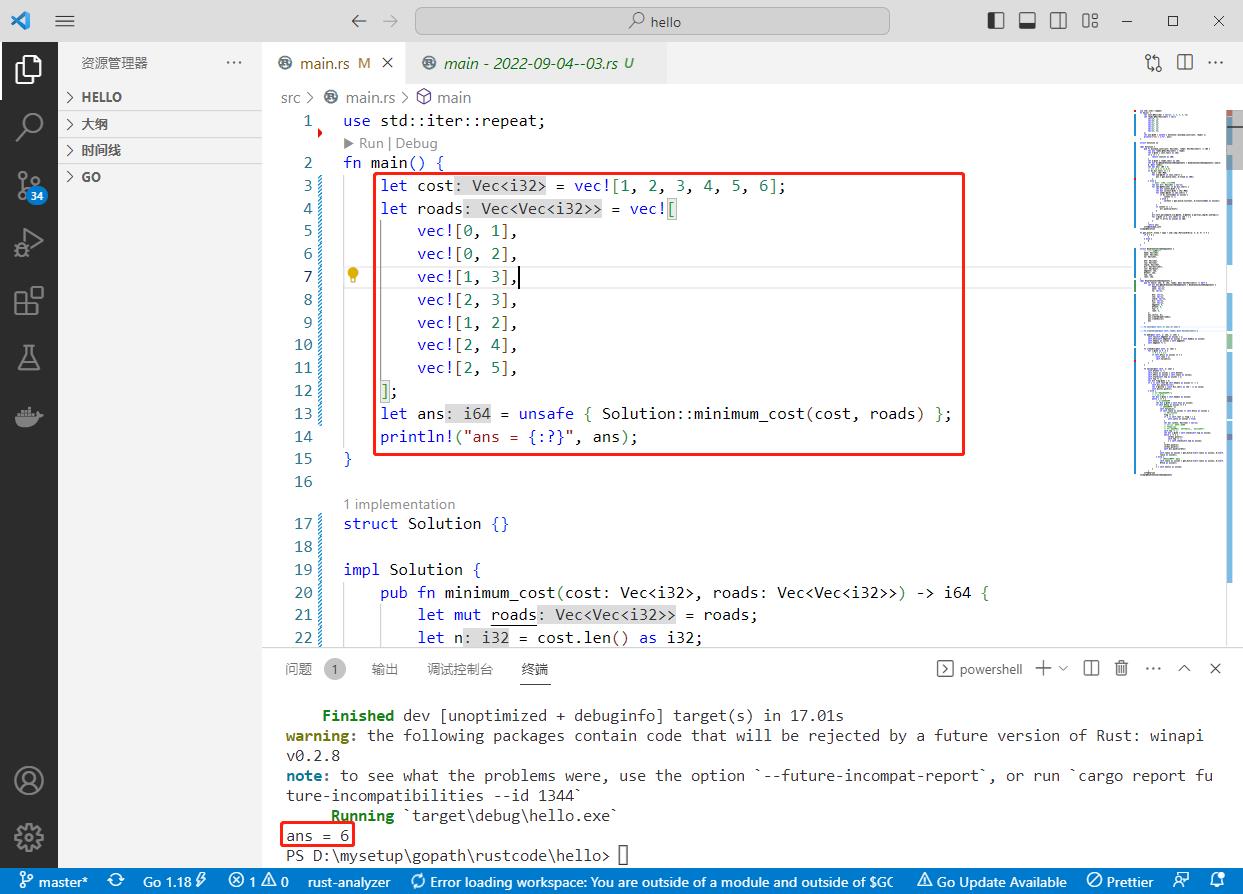
代码用rust编写。代码如下：

执行结果如下：

use std::iter::repeat;
fn main() 
    let cost = vec![1, 2, 3, 4, 5, 6];
    let roads = vec![
        vec![0, 1],
        vec![0, 2],
        vec![1, 3],
        vec![2, 3],
        vec![1, 2],
        vec![2, 4],
        vec![2, 5],
    ];
    let ans = unsafe  Solution::minimum_cost(cost, roads) ;
    println!("ans = :?", ans);


struct Solution 

impl Solution 
    pub fn minimum_cost(cost: Vec<i32>, roads: Vec<Vec<i32>>) -> i64 
        let mut roads = roads;
        let n = cost.len() as i32;
        if n == 1 
            return cost[0] as i64;
        
        let m = roads.len() as i32;
        let mut dc = DoubleConnectedComponents::new(n, m, &mut roads);
        let mut ans: i64 = 0;
        // dcc a,b,c c,d,e
        if dc.dcc.len() == 1 
            ans = i64::MAX;
            for num in cost.iter() 
                ans = get_min(ans, *num as i64);
            
         else 
            // 不只一个点双连通分量
            let mut arr: Vec<i32> = vec![];
            for set in dc.dcc.iter() 
                let mut cutCnt = 0;
                let mut curCost = i32::MAX;
                for nodes in set.iter() 
                    if dc.cut[*nodes as usize] 
                        cutCnt += 1;
                     else 
                        curCost = get_min(curCost, cost[*nodes as usize]);
                    
                
                if cutCnt == 1 
                    arr.push(curCost);
                
            
            arr.sort_by(|a, b| a.partial_cmp(b).unwrap());
            for i in 0..arr.len() as i32 - 1 
                ans += arr[i as usize] as i64;
            
        
        return ans;
    


fn get_min<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T 
    if a < b 
        a
     else 
        b
    


struct DoubleConnectedComponents 
    // 链式前向星建图
    head: Vec<i32>,
    next: Vec<i32>,
    to: Vec<i32>,

    dfn: Vec<i32>,
    low: Vec<i32>,
    stack: Vec<i32>,
    dcc: Vec<Vec<i32>>,
    cut: Vec<bool>,
    edgeCnt: i32,
    dfnCnt: i32,
    top: i32,
    root: i32,

impl DoubleConnectedComponents 
    pub fn new(n: i32, m: i32, roads: &mut Vec<Vec<i32>>) -> Self 
        let mut ans = DoubleConnectedComponents 
            head: vec![],
            next: vec![],
            to: vec![],

            dfn: vec![],
            low: vec![],
            stack: vec![],
            dcc: vec![],
            cut: vec![],
            edgeCnt: 0,
            dfnCnt: 0,
            top: 0,
            root: 0,
        ;
        ans.init(n, m);
        ans.createGraph(roads);
        ans.creatDcc(n);
        ans
    

    fn init(&mut self, n: i32, m: i32) 
        let t = repeat(-1).take(n as usize).collect::<Vec<i32>>();
        self.head = t;
        let t = repeat(0).take((m << 1) as usize).collect::<Vec<i32>>();
        self.next = t;
        let t = repeat(0).take((m << 1) as usize).collect::<Vec<i32>>();
        self.to = t;
        let t = repeat(0).take(n as usize).collect::<Vec<i32>>();
        self.dfn = t;
        let t = repeat(0).take(n as usize).collect::<Vec<i32>>();
        self.low = t;
        let t = repeat(0).take(n as usize).collect::<Vec<i32>>();
        self.stack = t;
        let t = repeat(false).take(n as usize).collect::<Vec<bool>>();
        self.cut = t;
        self.edgeCnt = 0;
        self.dfnCnt = 0;
        self.top = 0;
        self.root = 0;
    

    fn createGraph(&mut self, roads: &mut Vec<Vec<i32>>) 
        for edges in roads.iter() 
            self.add(edges[0], edges[1]);
            self.add(edges[1], edges[0]);
        
    

    fn add(&mut self, u: i32, v: i32) 
        self.to[self.edgeCnt as usize] = v;
        self.next[self.edgeCnt as usize] = self.head[u as usize];
        self.head[u as usize] = self.edgeCnt;
        self.edgeCnt += 1;
    

    fn creatDcc(&mut self, n: i32) 
        for i in 0..n 
            // 0 1 2 3 n-1
            if self.dfn[i as usize] == 0 
                self.root = i;
                self.tarjan(i);
            
        
    

    fn tarjan(&mut self, x: i32) 
        self.dfnCnt += 1;
        self.low[x as usize] = self.dfnCnt;
        self.dfn[x as usize] = self.low[x as usize];
        self.stack[self.top as usize] = x;
        self.top += 1;
        let mut flag = 0;
        if x == self.root && self.head[x as usize] == -1 
            self.dcc.push(vec![]);
            let t = (self.dcc.len() as i32 - 1) as usize;
            self.dcc[t].push(x);
         else 
            // 当前来到的节点是x
            // x a,b,c
            let mut i = self.head[x as usize];
            while i >= 0 
                // y是下级节点
                let mut y = self.to[i as usize];
                if self.dfn[y as usize] == 0 
                    // y点没遍历过！
                    self.tarjan(y);
                    if self.low[y as usize] >= self.dfn[x as usize] 
                        // 正在扎口袋
                        flag += 1;
                        if x != self.root || flag > 1 
                            self.cut[x as usize] = true;
                        
                        let mut curAns: Vec<i32> = vec![];
                        // 从栈里一次弹出节点
                        // 弹到y停！
                        // 弹出的节点都加入集合，x也加入，x不弹出
                        self.top -= 1;
                        let mut z = self.stack[self.top as usize];
                        while z != y 
                            curAns.push(z);
                            self.top -= 1;
                            z = self.stack[self.top as usize];
                        
                        curAns.push(y);
                        curAns.push(x);
                        self.dcc.push(curAns);
                    
                    self.low[x as usize] = get_min(self.low[x as usize], self.low[y as usize]);
                 else 
                    // y点已经遍历过了！
                    self.low[x as usize] = get_min(self.low[x as usize], self.dfn[y as usize]);
                
                i = self.next[i as usize];