数据结构 - 学习笔记 - 红黑树前传——234树

Posted 2023-01-19 笑虾

数据结构 - 学习笔记 - 红黑树前传——234树

• 简介
• 结点类型
• 与红黑树对应关系
• 插入逻辑
• • 插入步骤演示
  • 2结点插入
  • 3结点插入（红黑树旋转）
  • • 共对应6种红黑树情形
    • 有4种情形需要再平衡
  • 4结点插入（红黑树变色）
  • • 234树转红黑树
    • 触发分裂
    • 有4种情形需要变色实现平衡
    • 递归调整颜色
• 删除逻辑
• • 删除步骤演示
  • 234树删除结点
  • 2结点删除
  • 3结点删除
  • 4结点删除
• 辅助脚本
• 总结

简介

在学习红黑树前需要先了解234树。因为红黑树就是由234树演变出来的。
了解了234树才能明白红黑树颜色变化的底层逻辑。

1. 明明是包含123个结点，为什么不叫123树而叫234树。因为树的特性就是分叉，结点的命名是按它的分叉能力来的。我理解为：n结点就是能分n个叉的结点。（这怎么感觉跟制动有异曲同工之妙啊。）
2. 234树 就是 4阶B树。也就是允许结点最多有4个子结点的平衡多路查找树。
3. 234树 是倒着长的。新元素插入到叶子，然后触发分裂向上提升元素成父级。

结点类型

结点	结点内容	子结点 s	对应红黑树结点
2结点	1元素个。 如：a	2个子结点或无子结点 ( , a), (a, )	黑色a
3结点	2元素个。 如：a,b	3个子结点或无子结点 ( , a) , (a, b) , (b, )	父结点必需是黑色 黑色b—L→红色a 黑色a—R→红色b
4结点	3元素个。 如：a,b,c	4个子结点或无子结点 ( , a) , (a, b) , (b, c) , (c, )	红色a←L—黑色b—R→红色c

与红黑树对应关系

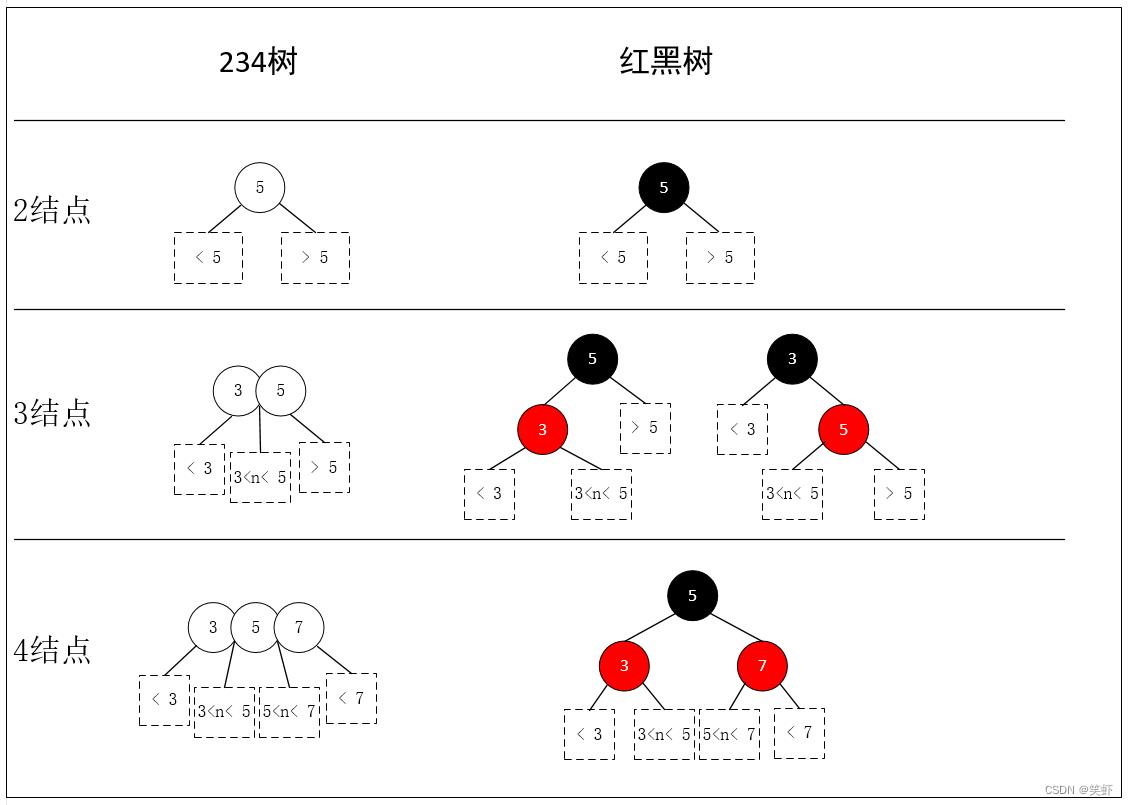
1. 上图中没有画出具体的子结点 仅用虚线框标识了一下子结点的取值范围。
2. 不难看出，只要将红黑树中的红结点向上一提，与父结点合并，就反推出了234树。
3. 在平时分析红黑树时，可以直接在脑海里映射成234树来分析。这样变化，旋转操作就有据可依，而不是死记硬背了。

插入逻辑

1. 新元素插入到叶子结点，如果触发分裂，再提取元素与上级合并。
2. 如果上提后，父级也触发分裂，则循环此操作，直到根结点。

插入场景	插入前	插入值	插入后	结论
当前无结点	空	1	[5]	直接插入就完事了。
当前2结点	[5]	3	[3, 5]	2结点升级为3结点。
当前3结点	[3, 5]	7	[3, 5, 7]	3结点升级为4结点。
当前4结点	[3, 5, 7]	8	[5] [3, 7, 8]	4结点 插入新值后，出现5结点的临时情况。 触发分裂：2 上升与原本的父结点合并。 1. 原本没有父结点，直接作为父结点。 2. 原父为2结点，合并。父结点变成3结点。 3. 原父为3结点，合并。父结点变成4结点。 4. 原父为4结点，合并。递归触发分裂。

插入步骤演示

下图演示了234树的插入步骤，以及触发分裂的效果。

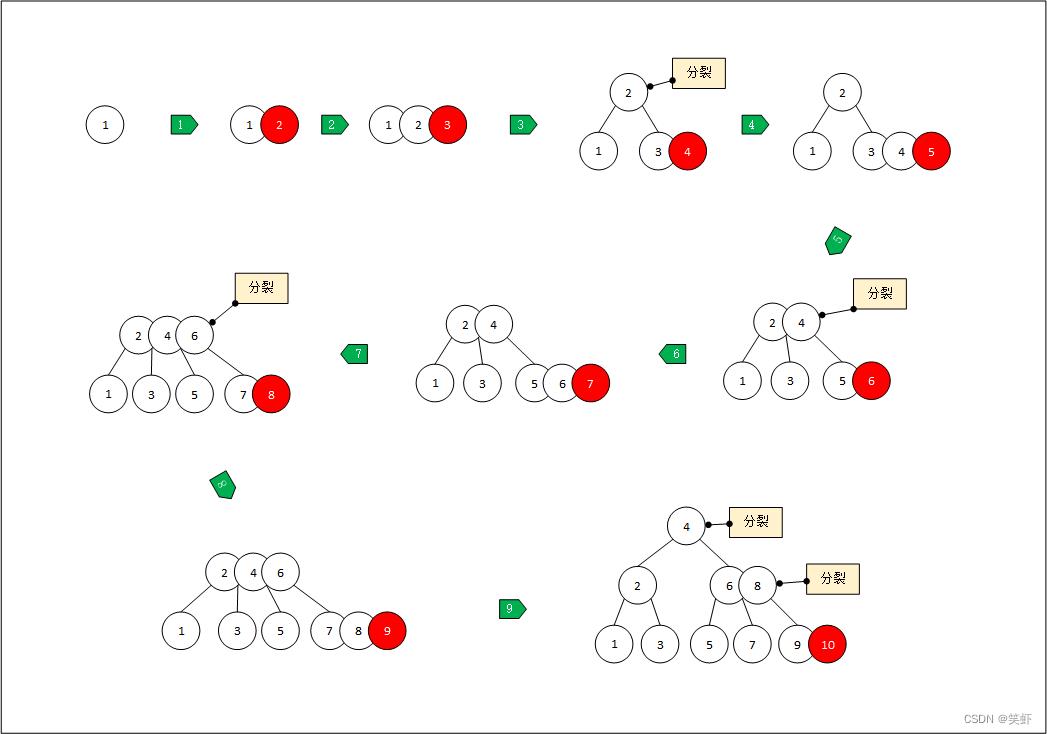
下图对应234树插入步骤，在右侧列出对应的红黑树。因为3结点转红黑树存在两种情况，所以按排列组合方式一一列出。
对照前文的与红黑树对应关系，可以看到黑红颜色背后的逻辑来源于234树。

2结点插入

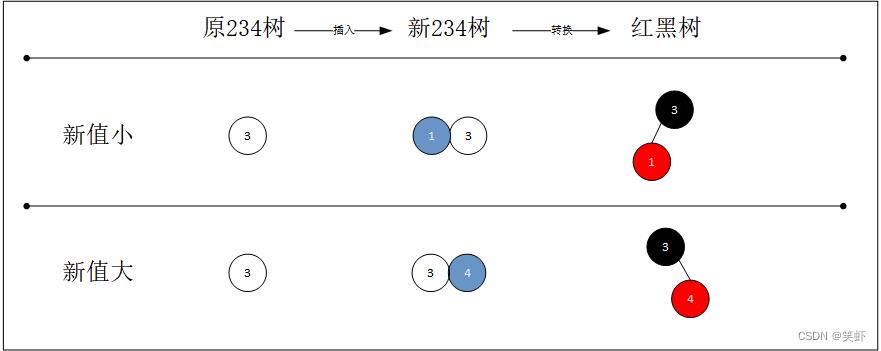
2结点插入新值，直接升级为3结点，无需任何调整。

3结点插入（红黑树旋转）

3结点插入新值，直接升级为4结点，无需任何调整。
但在3结点对应的红黑树中，可能出现不平衡的情况。需要旋转调整实现平衡。

共对应6种红黑树情形

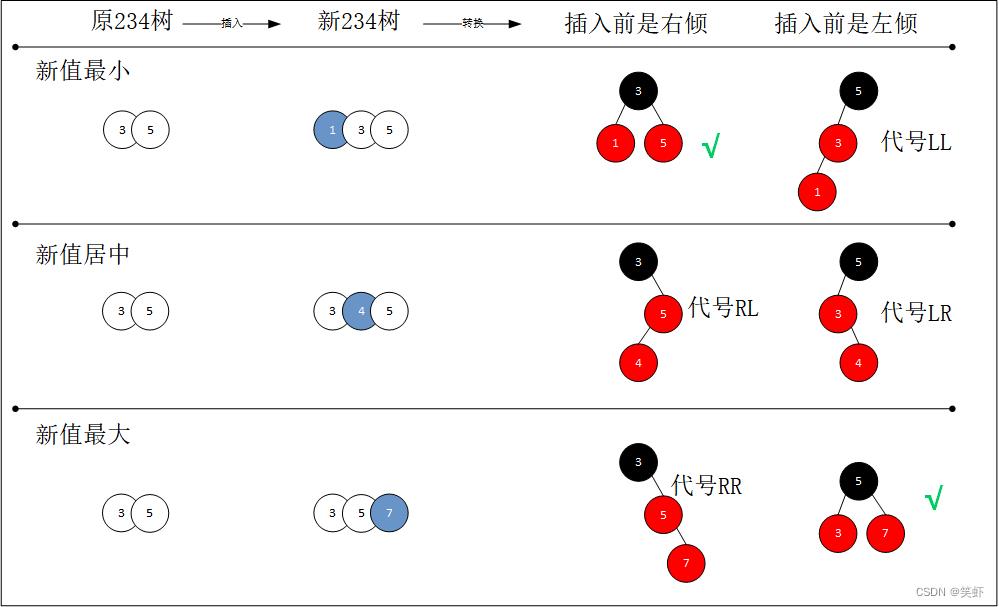
1. 旋转方向的逻辑可以想象天平。左边重了往右挪（旋），右边重了往左挪（旋）。
2. 从上图可以看到有3个位置能插入子结点。对应 6 种红黑树的情形。
3. 其中有2种是平衡的，无需调整。剩下4种 需要再平衡。

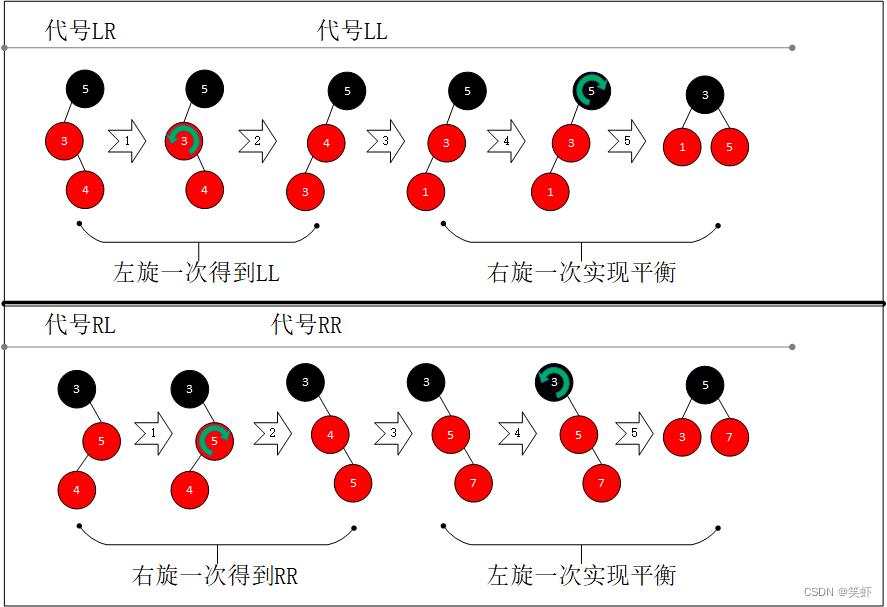
有4种情形需要再平衡

虽然共有4种 情形，但其中 LR可以转为LL， RL可以转为RR。总之就是有拐弯的，最终也是转为一条直线，再处理。

1. LL 右旋1次，实现平衡。
2. RR 左旋1次，实现平衡。
3. LR 左旋1次，转为 LL，重复 LL 的平衡操作。
4. RL 右旋1次，转为 LL，重复 RR 的平衡操作。
   

4结点插入（红黑树变色）

234树转红黑树

先简单的把 4结点 与 红黑树 对应关系，罗列出来。根据新结点插入的位置不同，对应的红黑树也有所差异：

对应上图的步骤序号。

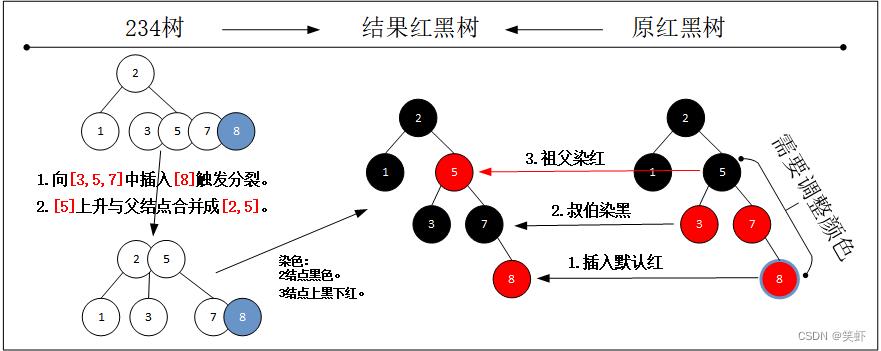
1. 原234树为 357.
2. 插入新元素。将要触发分裂。
3. 先分裂。然后找到目标位置，与原有的2结点 合并成为3结点
   3.1. 如果还有父结点，分裂出去的结点，与原父结点合并。
   3.2. 如果原来的父结点也是一个4结点，将递归触发分裂。
4. 234树结点转红黑树结点。
   4.1. 所有 2结点 变为黑色。
   4.2. 3结点 展开，上黑下红。

触发分裂

单独分析一下触发分裂效果。

1. 演示了从234树的角度来染色的逻辑（左）。
2. 演示了从红黑树的角度来染色的公式（右）。
3. 如果当前操作的只是一颗子树。比如结点2也是红色（需要旋转，对应RR公式），则需要继续处理，直至根。

有4种情形需要变色实现平衡

1. 【234树】 插入新元素。将要触发分裂。
2. 【234树】 先分裂。然后找到待插入的目标位置，与原有的2结点 合并成为3结点
3. 【红黑树】 这是一个中间状态，为了便于观察才把它画出来。（3结点展开，但未调色，暂时还保持着不平衡的状态，便于观察）
4. 【红黑树】 父结点、叔伯结点变成黑色，祖父结点变成红色。
   4.1. 父结点与祖父结点调换颜色：满足红结点子必黑的定义。同时对于插入新结点的这一路径来说黑结点数未发生变化。
   4.2. 叔伯结点变成黑色：祖父结点原本作为公共的黑结点，挪给左路后，右路就少了一个黑结点。因此 叔伯要站出来变黑维持平衡。
5. 【红黑树】 最后祖父结点更新为当前结点。
   5.1. 判断曾祖是否为红色。如果是，则需要向上递归调整颜色，一直到根。
   5.2. 如果是根，直接染黑。

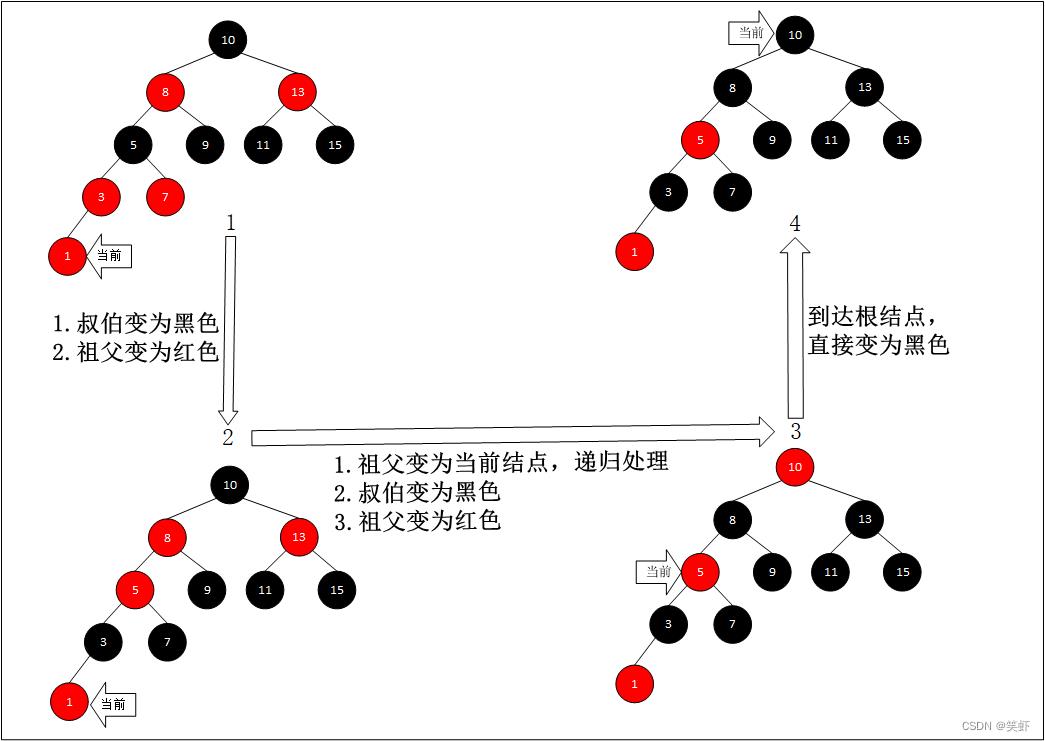
递归调整颜色

插入新结点 1 后递归触发变色。直到根结点为止。

删除逻辑

1. 先删除。（作为一颗二叉树，删除结点）
2. 再平衡。（作为一颗红黑树，调整颜色）

删除步骤演示

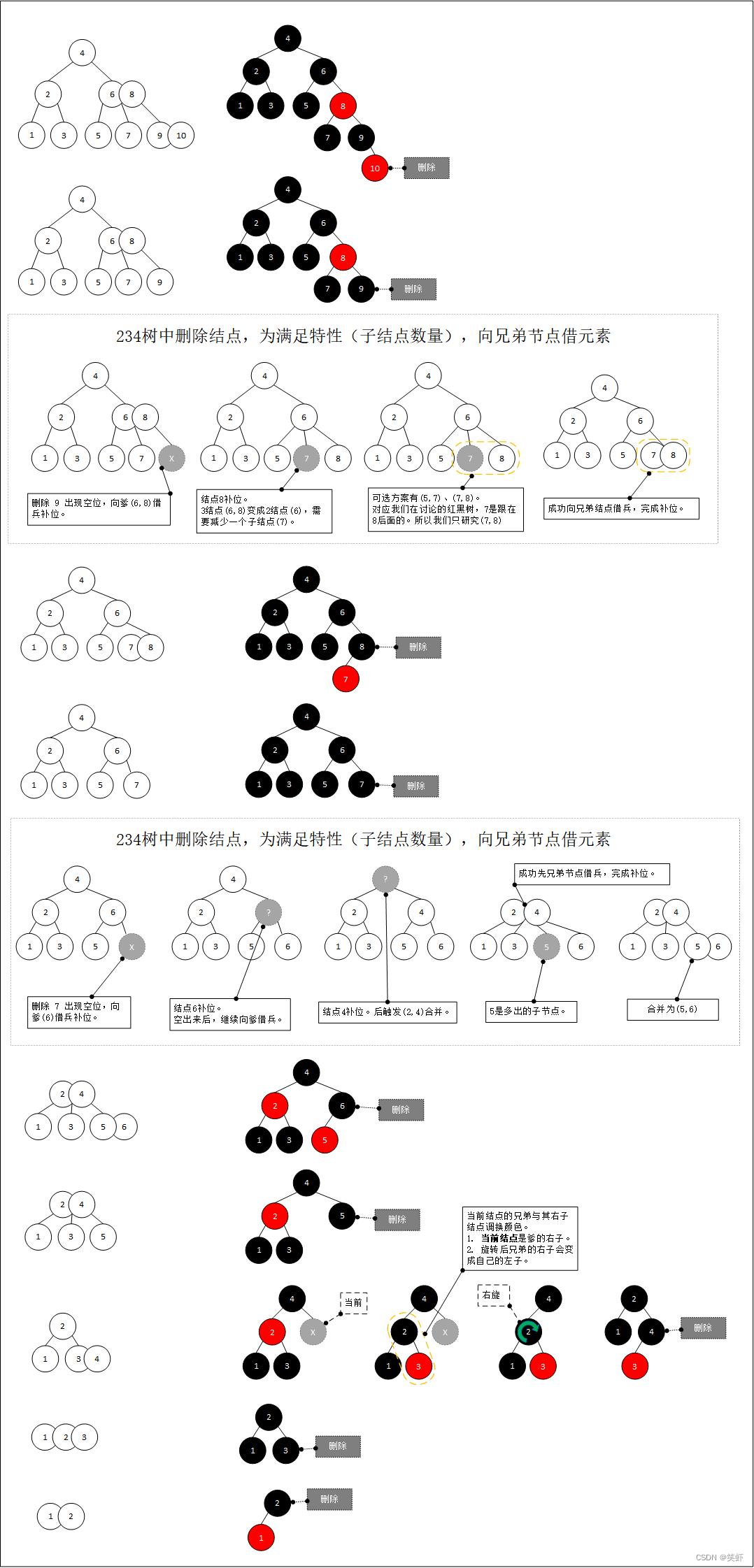
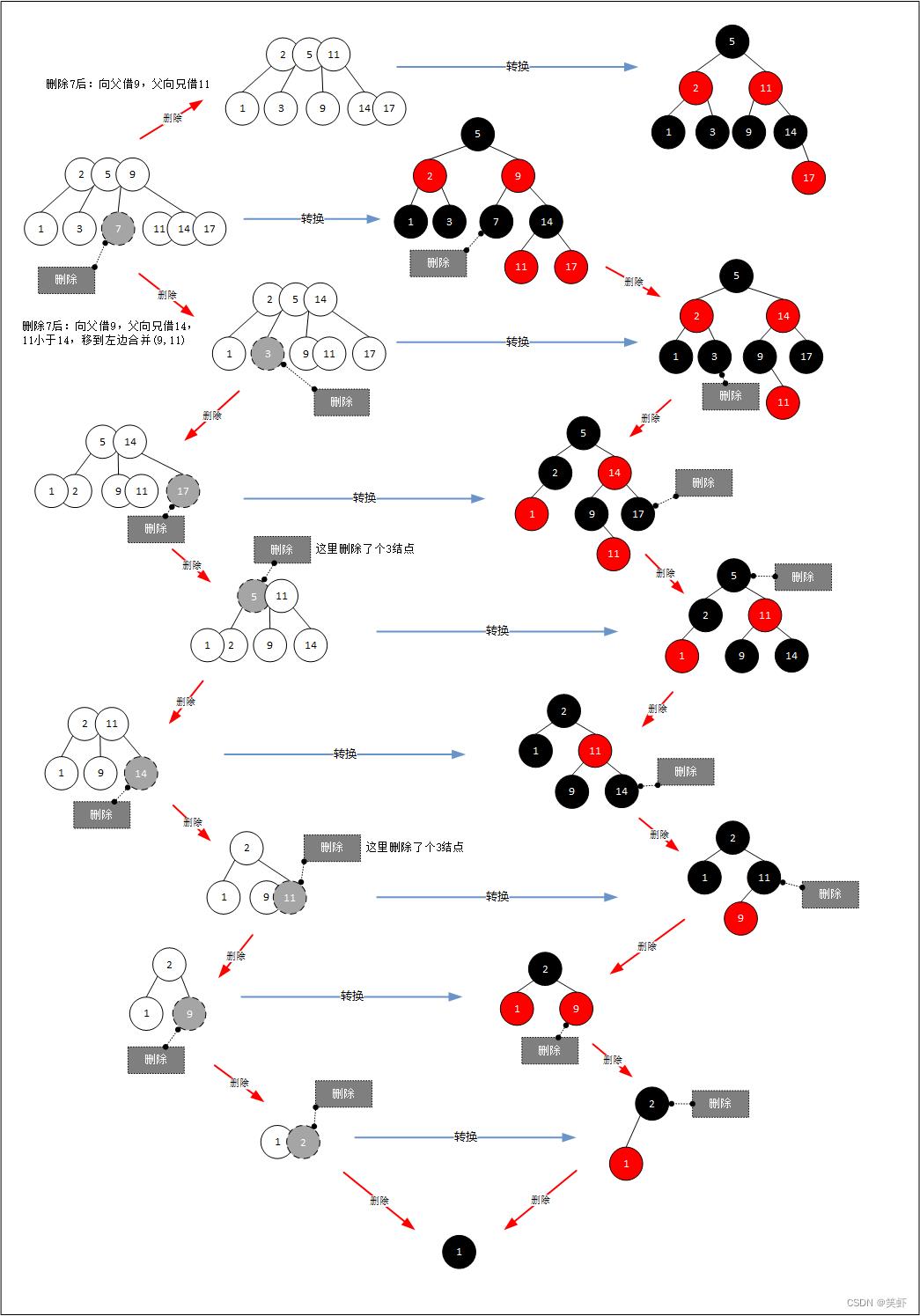
下图演示了234树的删除步骤，以及触发合并的效果。
同时，右则列表出对应的红黑树。
234树中删除结点，为满足特性（子结点数量），需要向父兄结点借元素。此过程可能会引发合并。下图中也用虚线框标出了借兵过程。

234树删除结点

234树删除结点时，根据被删除的结点所包含的子结点个数不同，共有3种场景：

结点	子结点数	删除操作
2结点	0个子结点	直接删除。
3结点	1个子结点	1. 删除当前结点。 2. 子结点顶上来。（还要染成黑色，维持平衡）
4结点	2个子结点	1. 找到前驱或后继结点。 2. 替换当前结点。 3. 再删除前驱或后继结点。

2结点删除

删除结点后，当前位置空出，红黑树失去平衡。需要向父兄结点借元素来补位。

3结点删除

删除一个元素，变成2结点。保持平衡。

• 红结点：直接删除即可。
• 黑结点：删除黑结点，红结点补位，并变成黑色。

1. 原234树结点，蓝色 标出是要删除的目标。
2. 转为对应的红黑树。
3. 删除目标结点。
4. 如果删的是父结点。子结点上移补位。
5. 补上来的结点染成原父结点的颜色。如果是根结点 直接填充黑色。

4结点删除

删除一个元素，变成3结点。保持平衡。
4结点 的删除，如果忽略掉它的兄弟结点。本质上还是一个3结点的删除。
对应红黑树：

• 红结点：直接删除即可。
• 黑结点：删除黑结点，红结点补位，并变成黑色。

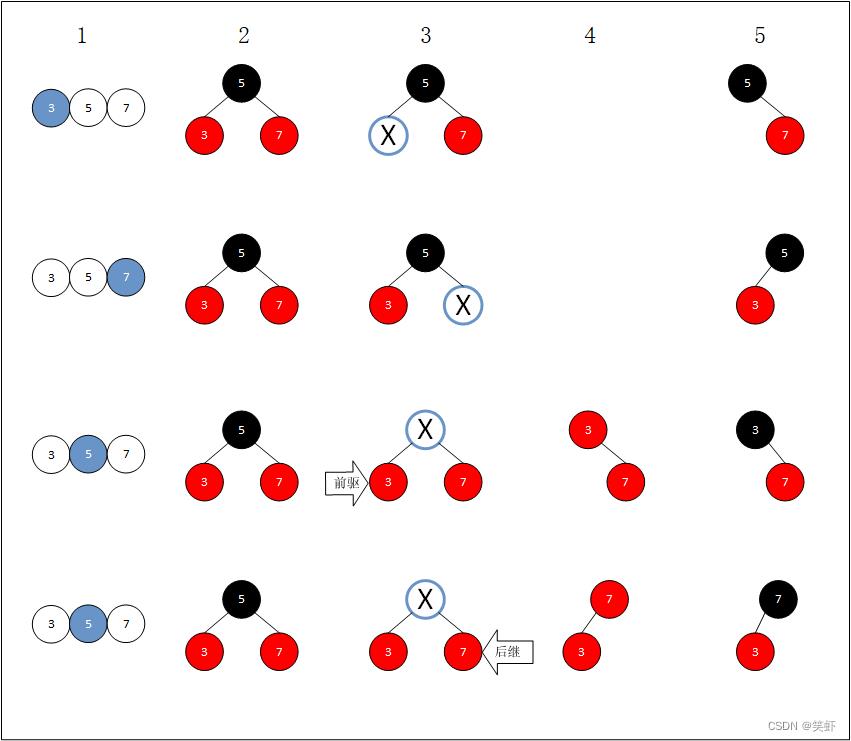
1. 234树结点，蓝色 标出是要删除的目标。
2. 转为对应的红黑树。
3. 删除目标结点。
4. 如果删的是父结点。子结点上移补位。
5. 补上来的结点染成原父结点的颜色。如果是根结点 直接填充黑色。（虽然单看234树转过来的这个局部，父结点必定是黑色。但在一个完整红黑中，父结点有可能是红色）

辅助脚本

红黑树可视化演示

var sleep = (delaytime = 1000) => 
  return new Promise(resolve => setTimeout(resolve, delaytime))

async function delayDo(arr, callback = data=>console.log(`数据：$data`), delaytime) 
    var len = arr.length;
    for (let i = 0; i <len  ; i++)         
        await sleep(delaytime);
        callback(arr[i]);
    
;
// 获取文本框
var [insertTxt, deleteTxt, findTxt] = [...document.querySelectorAll("#AlgorithmSpecificControls [type=Text]")];
// 获取按钮
var [insertBtn, deleteBtn, findBtn] = [...document.querySelectorAll("#AlgorithmSpecificControls [type=Button]")];
var process = 
	insert: function insert(v)	insertTxt.value = v; insertBtn.click();	,
	del: function del(v) deleteTxt.value = v; deleteBtn.click(); ,
	find: function find(v) findTxt.value = v; findBtn.click(); 

// 遍历数组，间隔 n 秒处理一个元素。
function main(arr = [...Array(10).keys()], cb = v=>console.log(v), delaytime=200)
	delaytime = delaytime<200 ? 200 : delaytime
    delayDo(arr, v => cb(v), delaytime);

// 插入元素，间隔 200 毫秒
main([...Array(20).keys()].map(v=>v+1), process.insert, 200);

总结

1. 可以将红黑树看作是234树的一个具体实现。
2. 一颗234树可以对应多个234树。（因为 3结点 对应 红黑树 时可以左倾，也可以右倾）