矩阵求特征值 和矩阵求逆 计算复杂度分析, 继续求助

Posted 2023-05-13

上次您给我解答了，可是貌似这样一个结论无法令别人信服，所以我还是需要更详细和准确的解答。请问你给我的那个关于o（n^3）的答案是如何得到的，具体它是计算次数，还是什么，另外，我需要具体算出 o（n^3）前面的系数，我应该如何做，具体可以参考什么数学书？

参考技术A 首先要明确，一般计算复杂度是针对算法的，而不是针对问题本身，对于问题本身的分析要复杂得多，远远超出你目前的知识范围。
一般稠密矩阵计算的各种算法复杂度都是O(n^3)，这个需要对每个算法都进行分析，我只是把各种结论归结起来告诉你。对于具体的算法而言，这个是数出来了，不需要很特别的技巧（某些含log的需要解递归，但这里一般不用），比如说m*k的矩阵和k*n的矩阵相乘，最平凡的算法的计算次数是2mnk，就是从下面的循环里数出来的
for
i=1:m
for
j=1:n
for
r=1:k
c(i,j)=c(i,j)+a(i,r)*b(r,j)
endfor
endfor
endfor
至于LU分解和Cholesky分解的计算次数分别是2/3*n^3和1/3*n^3，也是直接从循环里数出来的，不需要什么技巧。特征值的QR算法本质是迭代法，由于大致知道一般来讲总是很快进入局部的二次收敛，平均一个特征值需要2步（这个统计数据只适合于古典的Francis
QR），才能估计出具体的系数。
你最好是找一本矩阵计算的书自己先学一遍，不然我再多罗嗦也没用。

Python数值计算基础

note

scipy和numpy库可以便捷地进行科学计算，如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等。

文章目录

• note
• 一、多项式基础
• • 1. 1 多项式表示和拟合
  • 1.2 多项式插值
• 二、微积分计算
• • 2.1 数值积分
  • 2.2 符号积分
• 三、矩阵运算
• • 3.1 线性方程组的求解
  • 3.2 矩阵的特征值和特征向量
  • 3.3 矩阵求逆
  • 3.4 求解微分方程
• Reference

一、多项式基础

1. 1 多项式表示和拟合

# -*- coding: utf-8 -*-

import numpy as np
import math
import matplotlib.pyplot as plt

# i,j为基本虚数单位
print(1j)  # 虚数

# 无限大，结果还是inf无限大
a = np.inf
print(a / 10000)

# nan: 非数值
a = np.nan
print(a)

a = math.pi
print(a)

# 1.多项式表达方式
p = np.array([1, 0 ,-3, 5])
x = 3
# ex1: 将x=5代入y = x^3 - 3x + 5
print(np.polyval(p, x))
# ex2: 直接将向量代入
x = [1, 2, 3, 4, 5]
print(np.polyval(p, x))

# 2. 多项式求解, roots函数即求多项式的根
p = np.array([1, 0, -3, 5])
b = np.roots(p)
print(b)

# 3. 多项式乘法
a = [1, 2 , 3, 4]
b = [1, 4, 9, 16]
print(np.convolve(a, b))

# 4. 多项式拟合
x = [1, 2, 3, 4, 5]
y = [5.6, 38, 147, 240, 296]
p = np.polyfit(x, y, 3) # 三次多项式拟合
# 分析拟合结果
x2 = np.arange(1, 5.1, 0.1)
y2 = np.polyval(p, x2)
plt.plot(x, y, "*", x2, y2)
plt.show()

三次多项式拟合结果：

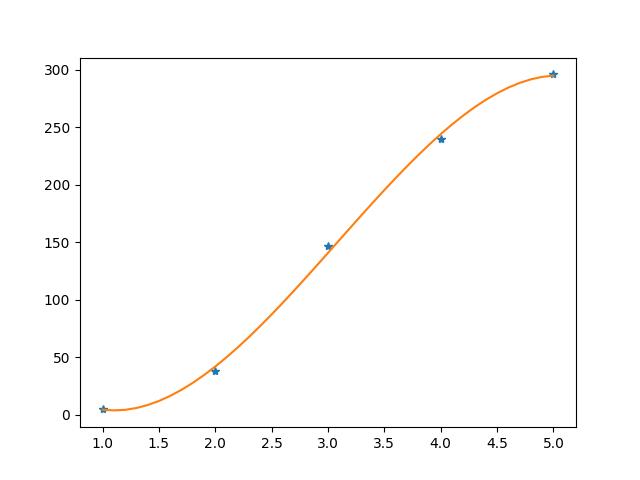
1.2 多项式插值

kind参数可以选择linear线性插值、cubic立方插值、spline三次样条插值等。

# -*- coding: utf-8 -*-
import numpy as np
import scipy.interpolate as itp
import matplotlib.pyplot as plt

# 年份从1900 到2000,间隔为10
year = range(1900, 2010, 10)
# 人口数量
number = 100 * np.sort(np.random.lognormal(0, 1, len(year)))
# 知道了1900,1910,……,2000年,每个10年的人口数量
# 通过插值方法获取1901或1999年人口的数据
x = np.array(range(1900, 2001))
# 采用样条插值方法
# y = np.interp(year, number, x)
y = itp.interp1d(year, number, kind="cubic")  # 多项式插值
y2 = y(x)
plt.plot(year, number, "*", x, y2)
plt.show()

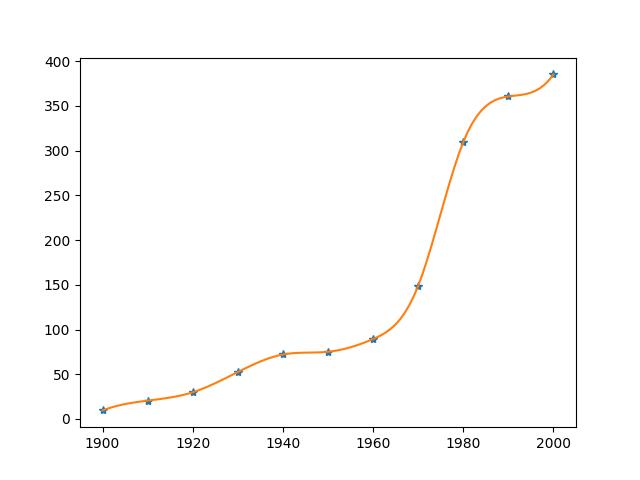
二、微积分计算

2.1 数值积分

求y = x^3 - 2x - 5的在[0, 2]上的积分。

# -*- coding: utf-8 -*-
import scipy.integrate
import math

F = lambda x: x ** 3 - 2 * x - 5
# 使用quad函数计算积分
Q = scipy.integrate.quad(F, 0, 2)
# 积分值
print(Q[0])

F = lambda y, x: y * math.sin(x) + x * math.cos(y)
# 使用dblquad函数计算积分 二重积分
Q = scipy.integrate.dblquad(F, math.pi, 2.0 * math.pi, lambda x: 0, lambda x: math.pi)
# 积分值
# Q= -9.8696

2.2 符号积分

计算二重积分$S={\int }_1^2{\int }_0^{1}xy\mathrm{d}x\mathrm{d}y$：

# -*- coding: utf-8 -*-
from sympy import *

# 定义符号变量
# 中间为空格,不能为逗号
x = Symbol('x', real=True)
y = Symbol('y', real=True)
# int(x*y,x,0,1)计算x*y,关于x在[0,1]上的积分,再计算函数关于y在[1,2]的积分
s = integrate(x * y, (x, int("0"), int("1")), (y, int("1"), int("2")))
# s=3/4
# int(x*y,x,0,1)计算x*y,关于x在[0,1]上的积分,再计算函数关于y在[1,2]的积分
# s = int(x * y, x, 0, 1)
s = integrate(x * y, (x, int("0"), int("1")))
ss = integrate(s, (y, int("1"), int("2")))

三、矩阵运算

3.1 线性方程组的求解

求解线性方程组：

# -*- coding: utf-8 -*-
import numpy as np

# 生成希尔伯特矩阵
def hilb(data):
    return 1.0 / (np.arange(1, data + 1) + np.arange(0, data)[:, np.newaxis])

a = hilb(3)
b = np.array([1, 2, 3])
a = a.T

x = np.linalg.lstsq(a, b)[0]
print(x)

3.2 矩阵的特征值和特征向量

• d, v = eig(A)
  • d为特征值
  • v为对应的特征向量

# -*- coding: utf-8 -*-
import numpy as np

# 生成服从正态分布的随机数矩阵
A = np.random.randn(4, 4)

# 调用eig函数,近似计算特征值与特征向量
d, v = np.linalg.eig(A)
print(d, "\\n")
print(v)

3.3 矩阵求逆

# -*- coding: utf-8 -*-
import numpy as np
A = np.random.randn(2, 2)
# A = np.ones(3, 3)
# 矩阵求逆
B = np.linalg.inv(A)
print(A, "\\n")
print(B, "\\n")
C = A * B
print(C, "\\n")
print(C.shape)

3.4 求解微分方程

以解常微分方程为例：可以使用scipy.integrate库进行数值积分和常微分方程组求解算法odeint。如计算洛伦兹吸引子的轨迹，洛伦兹吸引子有三个微分方程定义：

dx/dt=σ(y-x)
dy/dt=x(ρ-z)-y
dz/dt=xy-βz

三个方程定义了三维空间中各个坐标点上的速度矢量。从某个坐标开始沿着速度矢量进行积分，就可以计算出无质量点在此空间中的运动轨迹。其中 σ, ρ, β 为三个常数,不同的参数可以计算出不同的运动轨迹: x(t), y(t), z(t)。 当参数为某些值时,轨迹出现馄饨现象:即微小的初值差别也会显著地影响运动轨迹。下面是洛仑兹吸引子的轨迹计算和绘制代码：

#coding:utf-8
from scipy.integrate import odeint
import numpy as np


def lorenz(w,t,p,r,b):
    # 给出位置矢量w和三个参数p,r,b计算出
    #dx/dtt,dy/dt/dz/dt的值

    x,y,z=w

    #直接用lorenz的计算公式对应

    return np.array([p*(y-x),x*(r-z)-y,x*y-b*z])


t=np.arange(0,30,0.01) #创建时间点

#调用ode对lorenz进行求解，用两个不同的初始值
track1=odeint(lorenz,(0.0,1.00,0.0),t,args=(10.0,28.0,3.0))
track2=odeint(lorenz,(0.0,1.01,0.0),t,args=(10.0,28.0,3.0))


#绘图
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt


fig=plt.figure()
ax=Axes3D(fig)
ax.plot(track1[:,0],track1[:,1],track1[:,2])
ax.plot(track2[:,0],track1[:,1],track1[:,2])

plt.show()

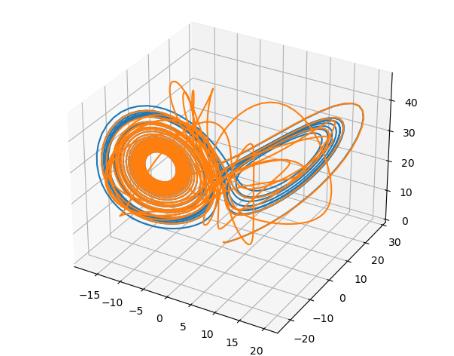
Reference

[1] 《用Python进行科学计算》——SciPy数值计算库