如何用python结合cplex求解混合整数规划问题

Posted 2023-05-12

参考技术A

第一步：注册IBM id账号
第二步：下载相关系统的CPLEX（windows/linux/mac）
这里需要系统中安装有JAVA，选择 open with Java web start launcher （需要下载JAVA），打开后就开始进入下载页面。
补充JAVA安装：
备注：JAVA可以通过rpm包安装，或者是bin文件安装。Rpm安装可以直接双击就可以打开jnlp后缀的文件，bin文件安装的话，需要在图形界面的命令行下执行：javaws ***.jnlp打开。我采用的是bin文件安装。
1、下载你想要的java版本压缩包。
JRE下载：
JDK下载：
2、对下载的文件进行解压
3、修改环境变量：

vim ~/.bashrc

#加入以下内容

export JAVA_HOME=/usr/lib/jvm/jdk1.8.0_144 
export JRE_HOME=$JAVA_HOME/jre  
export CLASSPATH=.:$JAVA_HOME/lib:$JRE_HOME/lib  
export PATH=$JAVA_HOME/bin:$PATH

#保存后使之生效  
source ~/.bashrc
第三步：下载完.bin文件后，修改文件的权限chmod +x filename.bin。然后用命令执行./filename.bin。进入安装。安装过程中需要设置安装路径，所以最好使用超级权限进行安装。默认路径为：/opt/ibm/ILOG/CPLEX_Studio_Community127
第四步：设置 CPLEX 的 Python API
CPLEX 的 Python API 属于 IBM ILOG CPLEX Optimization Studio 的一部分。
与CPLEX Python API 关联的模块驻留在目录 yourCPLEXhome/python/VERSION/PLATFORM 中（或文件夹 yourCPLEXhome\\python\\VERSION\\PLATFORM 中），此处 yourCPLEXhome 指定 CPLEX 安装为 IBM ILOG CPLEX Optimization Studio 一部分的位置，VERSION 指定与 CPLEX 兼容的 Python 版本，而 PLATFORM 表示操作系统与编译器的组合。
有两种可相互替代的方法来设置 CPLEX 的 Python API。
• 首选且最常用的方法是使用位于目录 yourCPLEXhome/python/VERSION/PLATFORM 中（或文件夹 yourCPLEXhome\\python\\VERSION\\PLATFORM 中）的脚本 setup.py。
• 或者，也可以将环境变量 PYTHONPATH 设置为 yourCPLEXhome/python/VERSION/PLATFORM 并通过 CPLEX 来开始运行 Python 脚本。
在以下段落中对这两种方法均进行了进一步详述。


使用脚本 setup.py
要在系统上安装 CPLEX-Python 模块，请使用位于 yourCplexhome/python/VERSION/PLATFORM 中的脚本 setup.py。 如果要将 CPLEX-Python 模块安装在非缺省位置，请使用选项 --home 识别安装目录。 例如，要将 CPLEX-Python 模块安装在缺省位置，请从命令行使用以下命令：
python setup.py install
要安装在目录 yourPythonPackageshome/cplex 中，请从命令行使用以下命令：
python setup.py install --home yourPythonPackageshome/cplex
这两个命令（缺省和指定主目录）均会调用 Python 包 distutils。 有关适用于该软件包的其他选项，请参考 Python distutils 的文档。


设置环境变量 PYTHONPATH
如果并行运行 CPLEX 的多个版本，那么请使用此方法：通过环境变量 PYTHONPATH 来向 Python 安装声明 CPLEX 及其 Python API 的位置。
要开始使用 CPLEX Python API，请将 Python 路径环境变量 PYTHONPATH 设置为值 yourCplexhome/python/VERSION/PLATFORM。 通过设置此环境变量，该版本的 Python 可以找到其所需的 CPLEX 模块以运行使用 CPLEX Python API 的 Python 命令和脚本。
后续步骤
通过这些可相互替代的方法之一设置 Python 环境后，便可以前进至启动 CPLEX Python API主题。




第五步：实例

Python -- version 2.7 
有3个不同求解方式：

execfile("cplexpypath.py")

import cplex
from cplex.exceptions import CplexError
import sys

# data common to all populateby functions
my_obj      = [1.0, 2.0, 3.0]
my_ub       = [40.0, cplex.infinity, cplex.infinity]
my_colnames = ["x1", "x2", "x3"]
my_rhs      = [20.0, 30.0]
my_rownames = ["c1", "c2"]
my_sense    = "LL"


def populatebyrow(prob):
prob.objective.set_sense(prob.objective.sense.maximize)

# since lower bounds are all 0.0 (the default), lb is omitted here
prob.variables.add(obj = my_obj, ub = my_ub, names = my_colnames)

# can query variables like the following bounds and names:

# lbs is a list of all the lower bounds
lbs = prob.variables.get_lower_bounds()

# ub1 is just the first lower bound
ub1 = prob.variables.get_upper_bounds(0)

# names is ["x1", "x3"]
names = prob.variables.get_names([0, 2])

rows = [[[0,"x2","x3"],[-1.0, 1.0,1.0]],
[["x1",1,2],[ 1.0,-3.0,1.0]]]

prob.linear_constraints.add(lin_expr = rows, senses = my_sense,
rhs = my_rhs, names = my_rownames)

# because there are two arguments, they are taken to specify a range
# thus, cols is the entire constraint matrix as a list of column vectors
cols = prob.variables.get_cols("x1", "x3")


def populatebycolumn(prob):
prob.objective.set_sense(prob.objective.sense.maximize)

prob.linear_constraints.add(rhs = my_rhs, senses = my_sense,
names = my_rownames)

c = [[[0,1],[-1.0, 1.0]],
[["c1",1],[ 1.0,-3.0]],
[[0,"c2"],[ 1.0, 1.0]]]

prob.variables.add(obj = my_obj, ub = my_ub, names = my_colnames,
columns = c)

def populatebynonzero(prob):
prob.objective.set_sense(prob.objective.sense.maximize)

prob.linear_constraints.add(rhs = my_rhs, senses = my_sense,
names = my_rownames)
prob.variables.add(obj = my_obj, ub = my_ub, names = my_colnames)

rows = [0,0,0,1,1,1]
cols = [0,1,2,0,1,2]
vals = [-1.0,1.0,1.0,1.0,-3.0,1.0]

prob.linear_constraints.set_coefficients(zip(rows, cols, vals))
# can also change one coefficient at a time

# prob.linear_constraints.set_coefficients(1,1,-3.0)
# or pass in a list of triples
# prob.linear_constraints.set_coefficients([(0,1,1.0), (1,1,-3.0)])


def lpex1(pop_method):
try:
my_prob = cplex.Cplex()

if pop_method == "r":
handle = populatebyrow(my_prob)
if pop_method == "c":
handle = populatebycolumn(my_prob)
if pop_method == "n":
handle = populatebynonzero(my_prob)

my_prob.solve()
except CplexError, exc:
print exc
return

numrows = my_prob.linear_constraints.get_num()
numcols = my_prob.variables.get_num()

print
# solution.get_status() returns an integer code
print "Solution status = " , my_prob.solution.get_status(), ":",
# the following line prints the corresponding string
print my_prob.solution.status[my_prob.solution.get_status()]
print "Solution value  = ", my_prob.solution.get_objective_value()
slack = my_prob.solution.get_linear_slacks()
pi    = my_prob.solution.get_dual_values()
x     = my_prob.solution.get_values()
dj    = my_prob.solution.get_reduced_costs()
for i in range(numrows):
print "Row %d:  Slack = %10f  Pi = %10f" % (i, slack[i], pi[i])
for j in range(numcols):
print "Column %d:  Value = %10f Reduced cost = %10f" % (j, x[j], dj[j])

my_prob.write("lpex1.lp")

if __name__ == "__main__":
if len(sys.argv) != 2 or sys.argv[1] not in  ["-r", "-c", "-n"]:
print "Usage: lpex1.py -X"
print "   where X is one of the following options:"
print "      r          generate problem by row"
print "      c          generate problem by column"
print "      n          generate problem by nonzero"
print " Exiting..."
sys.exit(-1)
lpex1(sys.argv[1][1])
else:
prompt = """Enter the letter indicating how the problem data should be populated:
r : populate by rows
c : populate by columns
n : populate by nonzeros\\n ? > """
r = 'r'
c = 'c'
n = 'n'
lpex1(input(prompt))

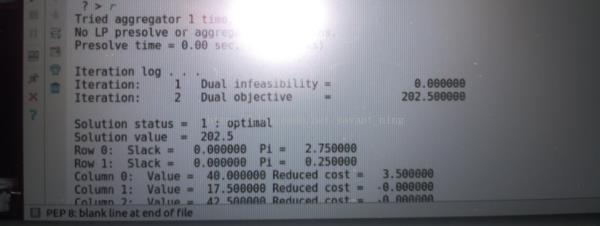
选择r参数，求解结果如下： 

混合整数线性规划

当上一节讲到的线性规划问题中，要求某些变量是整数的时候，就变成了混合整数线性规划问题。

其实对于某些问题来说，线性规划问题的最优解刚好是整数，那么它对应的混合整数线性规划问题的解就刚好是这个最优解了。因此分支限界法的思路是，

1. 将原混合整数线性规划问题改进为行的松弛问题，不断地用单纯形法求解

2. 

3. 直到整数最优解出现在新的改进后的松弛问题的一个顶点。

 

例如对于以下问题，

\\[\\begin{array}{*{20}{l}}
{\\max 3x + y + 3z}\\\\
{2x + 2y + z \\le 30}\\\\
{1.5x + 2y + 3z \\le 25}\\\\
{2x + y + z \\le 20}\\\\
{x \\ge 0,y \\ge 0,z \\ge 0,}
\\end{array}\\]

最优解obj=36.6667，x=7.7778，y=0，z=4.4444，怎么求它的整数最优解呢？

针对该线性松弛问题得到的最优解，选取非整数解的整数变量x，将原线性松弛问题分成两个子问题，其中一个子问题加上x≤7的约束，另一个子问题加上x≥8的约束。

针对x≤7的这个子问题，求得最优解为obj=35.5，x=7，y=0，z=4.8333。选取非整数解的整数变量z，将该问题拆成z≤4和z≥5的两个子问题。

针对z≤4的这个子问题，求得最优解为obj=34.25，x=7，y=1.25，z=4。选取非整数解的整数变量y，将该问题拆成y≤1和z≥2的两个子问题。

针对y≤1的这个子问题，求得最优解为obj=34，x=7，y=1，z=4。

按照上述步骤，求另外对应的子问题。

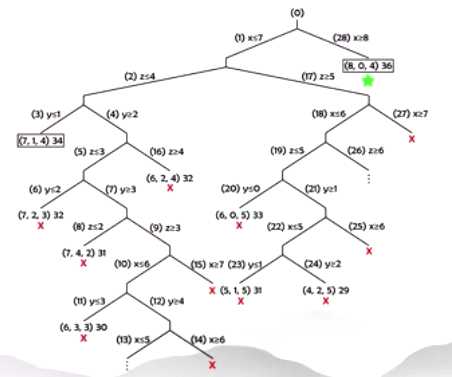
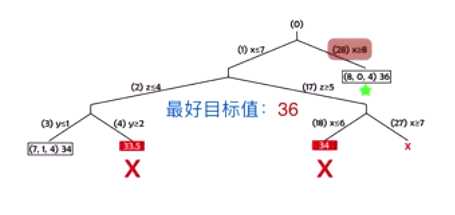
在分支过程中，当

1. 问题是不可满足的

2. 最优解是整数值

3. 松弛问题的最优值比当前最优值更差

无需深入探索，可以剪枝。

 

 

 

参考：

https://www.coursera.org/lecture/lisan-youhua-suanfapian/3-3-2-hun-he-zheng-shu-xian-xing-gui-hua-PQhnK