Opencv2.4.9源码分析——Stitching
Posted zhaocj
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Opencv2.4.9源码分析——Stitching相关的知识，希望对你有一定的参考价值。
2、计算单应矩阵
2.1 原理
在得到了图像特征点以后，我们就可以根据这些特征点，实现图像匹配，即得到重叠区域。而要把多幅图像拼接成一幅图像，就需要以某幅图像为基准，把其他图像映射到该图像所在的平面。映射的关键所在就是根据重叠区域的特征点计算图像间的单应矩阵。
我们可以通过最近邻算法（K-NN，这里的K表示最近邻特征点的数量）得到与图像A中的某一特征点a最相似的其他任意一幅图像B的K个特征点，对这K个特征点进行距离比较来最终判断是否找到了a的最相似特征点，即配对成功与否。例如我们这里选择K为2，即2-NN算法，图像B中的与a最相似的两个特征点为b和c，设Lab和Lac分别表示a与b和c的距离（距离是通过特征点描述符的比较实现的），并且Lab＜Lac，如果满足下式，则我们认为a的匹配特征点为b：
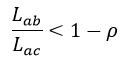（1）
式中，ρ表示匹配阈值。
那么如何得到这K个特征点呢？最简单、也是最粗暴的方法就是计算a与图像B中的所有特征点的距离，这种方法适用于特征点不多的情况。当特征点较多，并且需要匹配的图像也较多时，应用K-D树（K-维树）的算法会更有效。
K-D树是一棵二叉树，树中存储的是一些K维数据，这正好对应于特征点的K维描述符。K-D树本质上是对该K维数据集合的一种K维空间的划分，即树中的每个叶节点都对应于一个K维超矩形区域。当K-D树构建好后，可以很迅速的得到某一数据所属的超矩形区域。所以K-D树非常适合范围搜索和最近邻搜索，但它不适合维数太多的数据搜索。另外，需要注意的是K-NN中的K和K-D树中的K表示的含义是不同的。
首先我们需要利用已知数据构建K-D树（这里的数据指的是图像B中的所有特征点，而特征点是用描述符表示的）。要想构建K-D树，需要解决两个问题：第一是选择哪个维度进行分割；第二是如何把数据分割为左分支和右分支。对于第一个问题，通常的做法是交替循环的依次选择所有的维度，例如在3-D树中，“父节点”用的x维，则“子节点”用y维，“孙节点”用z维，“重孙节点”又回到x维，“重重孙节点”用y维，以此类推。对于第二问题，一般的做法是选择该维度的中值进行分割，小于该值的数据归为左分支，大于该值的数据归为右分支。以上方法可以保证K-D树是平衡的，即每个叶节点与根节点的距离基本相同。
当K-D树构建好了以后，我们就可以搜索待查询数据（这里指的是图像A中的特征点a）的最近邻数据，它的过程是：从根节点出发，依据分叉规则（即选择分割维度和比较中值），沿着搜索路径达到最佳叶节点；然后再从该叶节点出发，回溯搜索路径，找到是否有比最佳叶节点更好的节点，用以替代它。从概念上来说，回溯的过程就是以待查询点为中心，以待查询点到最佳叶节点的距离为半径，画一个超球体，如果该超球体与分割维度所在的超平面相交，则需要搜索该超平面的另一侧（即另一个分支），如果不相交，则无需再搜索另一侧。
特征点的匹配点对得到后，我们就可以利用这些匹配点对评估计算图像间的单应矩阵H。
如果平面到平面之间的映射关系是投影映射的话，那么一定存在一个非奇异的3×3的矩阵H，当p表示一个平面的任意一点时，那么该点映射到另一平面的点就为Hp。当相机围绕一点进行旋转而得到不同的两幅图像时（如图3所示），这两幅图像之间就是投影映射，它们之间的关系就可以用矩阵H来进行描述，即图像A中的点通过矩阵H就可以映射到图像B中，从而实现两幅图像的拼接。
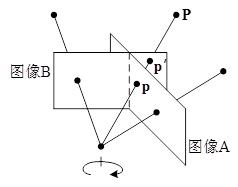
图3 通过旋转相机，得到不同的图像
需要指出的是，当矩阵H乘以任意一个不为零的常数时，并不改变两个平面之间的投影映射关系，因此H被认为是只有8个自由度的单应矩阵。
设图像A中的某一点的齐次坐标p为(u, v,1)，该点在图像B中的匹配点的齐次坐标p’为(u’, v’,1)，则：
（2）
即
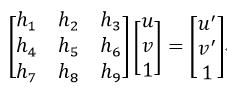（3）
图像坐标(x, y)所对应的齐次坐标为(x, y, 1)，而齐次坐标(x, y, z)所对应的图像坐标为(x/z, y/z)。
我们把式3展开，则：
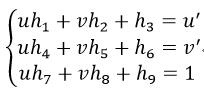（4）
把式4写成矩阵的形式：
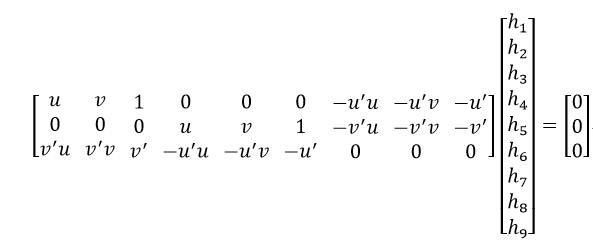（5）
我们观察式5等号左侧的第一个矩阵会发现，第三行是前两行的线性组合，即
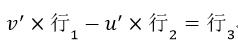（6）
因此式5应改为
（7）
一对匹配点对可以列写两个方程，那么要想求解只有8个自由度的矩阵H只需要四个匹配点对即可，但要求这四对点每三个都不能共线：
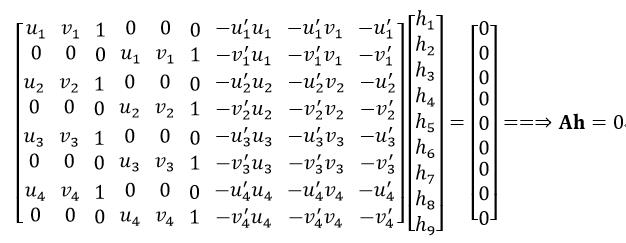（8）
式中，h是矩阵H的向量形式。Ah＝0被称为齐次线性最小二乘问题，因此求解单应矩阵H就转换为齐次线性最小二乘问题。该方法也称为直接线性变换（DLT）。
式8表示的是一个齐次线性方程组，式中A为矩阵，h为相量，我们需要求非零的h。而h属于A的零空间，有时也称为A的零（右）相量，因此h可以由A的奇异值分解（SVD）得到，也就是说并不需要解方程组就可以得到h。A的奇异值分解形式为：
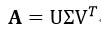（9）
则h为V的最后一列，再把h重新整理，就可得到H。
通过式9得到h的方法非常依赖于图像的坐标原点及尺度，这会使算法不稳定，产生数值误差。但我们可以通过归一化的方法使数值收敛于正确的结果。归一化的方法是首先平移图像坐标，使图像的坐标原点为匹配点对的重心；然后是改变尺度，使匹配点到平移后的坐标原点的距离为1。匹配点对所在的两幅图像，以及它们的横、纵坐标都必须分别独立的进行上述归一化处理。归一化的具体计算过程为：
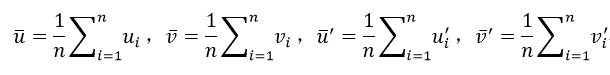（10）
式中，n表示匹配点对，这里n为4，该式得到了坐标平均值，即坐标平移量。
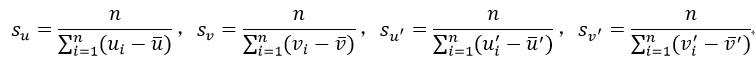（11）
式11得到了坐标尺度，即匹配点到原点的距离为1，如果想使距离为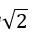 
（许多文献上，此处的值都是 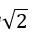，Opencv用的是1），则只需再乘以 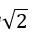即可。由式10和式11分别构成两个坐标变换矩阵：
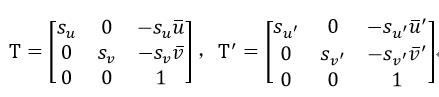（12）
则两幅图像的坐标分别变为：
（13）
即
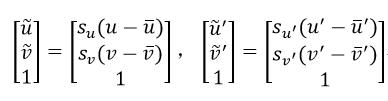（14）
这时，我们就需要用坐标变换后的4个匹配点对计算单应矩阵，得到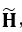
，它与真实坐标下的H的关系为：
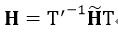（15）
式中的T’-1很容易由式12中的T’得到：
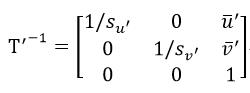（16）
下面我们给出归一化直接线性变换的步骤：
●由式10和式11分别计算平移量和尺度；
●由式12计算坐标变换矩阵；
●由式13计算坐标变换后的特征点坐标值，并代入式8得到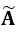
，再经过奇异值分解（式9）得到 ；
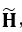●由式15得到最终的单应矩阵H。
以上是由4个匹配点对计算出单应矩阵H，为了增加鲁棒性，可以用更多的匹配点对计算H。此时式8就是一个超定方程组，因为A是2n×9的矩阵，而n>4，所以2n>9。当匹配点对n的数量很大时，直接用SVD的方法就不是很方便，这时我们就可以直接应用最小二乘法求解。因为Ah＝0，它的误差平方函数f(h)可以写为：
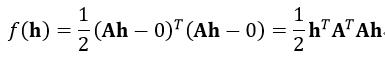（17）
很显然，我们应该使f(h)最小，此时的h即为求解。因此我们对f(h)求导，并使导数为0，则
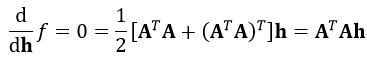（18）
ATA是对称的9×9的方阵，我们对ATA进行特征值分解，则h应该是ATA的特征值为0所对应的特征向量，当然因为存在误差，有时会出现没有一个特征值为0的情况，这时h等于最接近0的特征值所对应的特征向量。可以很容易的证明，对A进行奇异值分解与对ATA进行特征值分解得到的h是完全相等。因此特征值分解的方法也适用于n＝4的情况。
尽管使用了更多的匹配点对，但由于误差的存在，匹配点对的位置可能会出现偏差，即有好的匹配点对（称之为内点），也有不好的匹配点对（称之为外点）。如果用外点计算，则H肯定是不正确的，所以我们应该选择内点。那么如何区分内点和外点呢？通常的做法是应用RANSAC（随机抽样一致性，RANdom SAmple Consensus）算法。
RANSAC算法的核心思想是从样本集中抽取多少次才能保证至少有一次不是外点的概率为q。则据此，可以得到下列关系式：
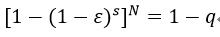（19）
式中，N表示抽取的次数，ε表示样本集中外点的比例，s表示每一次抽取样本的数量，在这里s为4，因为求单应矩阵H至少需要4个匹配点对，因此我们需要每一次抽取4个匹配点对。式19又可以表示为：
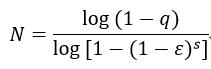（20）
式中，q是需要事先确定的参数，q越大，得到的内点就越可信。ε由重映射误差的方法得到，即当得到了单应矩阵H后，可以把图像A中的特征点p重映射到图像B中，计算映射后的点与它的匹配点对的特征点p’之间的几何距离：
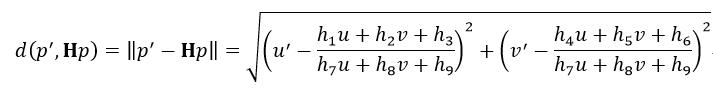（21）
而重映射误差为d2(p’,Hp)。如果该距离小于事先确定好的阈值η，则认为这对匹配点对是内点，否则是外点。计算所有的匹配点对，这样就可以统计出内点和外点的数量，从而得到ε，进而由式20得到N。
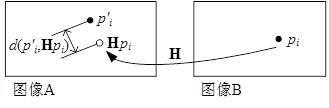
图4 重映射误差
下面我们给出RANSAC计算单应矩阵H的步骤：
●给出参数q和η，以及迭代次数N；
●进入迭代，一共需迭代N次：
▲ 随机抽取4个匹配点对，要求任意3个不共线；
▲ 由归一化直接线性变换计算单应矩阵H；
▲ 由重映射误差方法（式21）计算内点的数量，并得到参数ε；
▲ 由式20更新最大迭代次数N；
●在迭代循环内已得到最大的内点数量，由这些内点计算单应矩阵，得到最终的H。
另外，我们还需要用下列的关系式来说明内点数ni和匹配点对数量nf之间的关系：
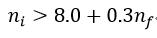（22）
如果满足式22，则说明图像间有很好的匹配。或者我们用一个匹配置信度c来衡量：
（23）
c越大越好，当然如果c大于3（3为实验数据），则认为这两幅图像十分接近，可以被看成是一幅图像了；而如果c小于一定的值，则认为这两幅图像没有重叠的区域，所以就无法拼接在一起。
应用RANSAC算法的主要目的是得到内点，而用全体内点经过特征值分解计算得到的H误差较大，可以说比较粗糙，因此我们还需要用更加“精细”的方法得到精确的H。由式21可知，H应该使重映射误差（即匹配点对之间的几何距离）达到最小。因此这是一个参数优化估计求极值的问题。基于LM算法（Levenberg-Marquardt）的优化是目前应用较为广泛的一种无条件约束优化方法，该算法是在逼近某个极小点时平方收敛，因此它是专门用于误差平方和最小化的方法。该算法的特点是，它是高斯牛顿法和梯度下降法的结合，既有高斯牛顿法的快速收敛性，也有梯度下降法的全局搜索特性。
下面我们就给出应用LM算法计算H的方法。
首先给出误差指标函数，即所有内点的重映射误差的平方和：
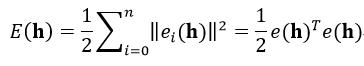（24）
式中，n表示内点的总数，h是单应矩阵H的向量形式，第i对匹配点对的重映射误差ei为：
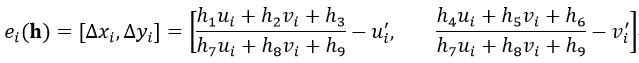（25）
而e(h)则为：
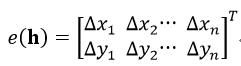（26）
LM算法用于迭代计算h的公式为：
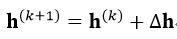（27）
式中，h的上标表示迭代的次数，步长∆h为：
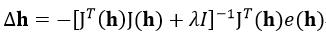（28）
式中，I为单位矩阵，λ为大于0的常数，如果λ为0，则LM算法为高斯牛顿法，如果λ取值很大，则LM算法接近梯度下降法。因此当每迭代成功一步时，需把λ减小一些，这样在接近误差目标的时候，逐渐与高斯牛顿法相似。J(h)为式24的E(h)的雅可比矩阵（Jacobian矩阵），我们在前面已分析过了，H是只有8个自由度的单应矩阵，所以我们可以把H进行归一化处理，使h9为1，则J(h)只需对H中前8个元素求偏导数：
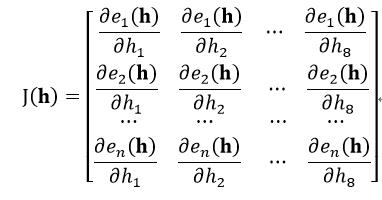（29）
式中，n表示待拼接的图像数量。
下面我们就分别给出ei(h)（式25，其中h9＝1）对h的偏导数：
（30）
由于ei(h)是由横坐标和纵坐标两个值组成的，因此在计算E(h)（式24）和∆h（式28）时，先分别对横、纵坐标单独进行相关运算，然后再把横、纵坐标下的两个值相加。
下面我们给出LM算法计算h的步骤：
●把RANSAC最后计算得到的h作为LM算法的初始h，并初始化λ为0.001；
●进入迭代，当满足最大迭代次数或∆h小于一定程度（即误差目标函数变化很小）时，退出迭代；
▲ 由式28计算∆h；
▲比较E(h+∆h)和E(h)的大小，如果E(h+∆h)小于E(h)，则h←h+∆h，λ←λ/10；如果E(h+∆h)大于E(h)，则λ←10λ。
2.2 源码
class detail::FeaturesMatcher表示特征匹配：
class CV_EXPORTS FeaturesMatcher
public:
virtual ~FeaturesMatcher()
//两个重载( )运算符
//第一个重载( )运算符负责的是两幅图像之间的匹配，它主要是调用match函数，features1和features2分别表示待匹配的两幅图像的特征，matches_info表示匹配信息
void operator ()(const ImageFeatures &features1, const ImageFeatures &features2,
MatchesInfo& matches_info) match(features1, features2, matches_info);
//第二个重载( )运算符负责的是所有待拼接图像的匹配，它可以实现并行处理，在执行的过程需要调用第一个重载( )运算符
void operator ()(const std::vector<ImageFeatures> &features, std::vector<MatchesInfo> &pairwise_matches,
const cv::Mat &mask = cv::Mat());
//判断是否能够进行并行处理
bool isThreadSafe() const return is_thread_safe_;
virtual void collectGarbage() //释放已被分配、但还没有被使用的内存
protected:
FeaturesMatcher(bool is_thread_safe = false) : is_thread_safe_(is_thread_safe)
//虚函数，调用子类BestOf2NearestMatcher的match函数，即应用2-NN方法实现匹配，目前只实现了该方法的匹配
virtual void match(const ImageFeatures &features1, const ImageFeatures &features2,
MatchesInfo& matches_info) = 0;
bool is_thread_safe_; //表示是否可以进行并行处理
;
FeaturesMatcher类的第二个重载( )运算符：
void FeaturesMatcher::operator ()(const vector<ImageFeatures> &features, vector<MatchesInfo> &pairwise_matches,
const Mat &mask)
//features表示所有图像的特征
//pairwise_matches表示两幅图像之间的匹配信息
//mask表示图像掩码，指出哪些图像不参与匹配
const int num_images = static_cast<int>(features.size()); //得到待拼接的图像数量
//确保图像掩码的格式正确
CV_Assert(mask.empty() || (mask.type() == CV_8U && mask.cols == num_images && mask.rows));
Mat_<uchar> mask_(mask); //复制
if (mask_.empty()) //都置1，表示都进行匹配
mask_ = Mat::ones(num_images, num_images, CV_8U);
vector<pair<int,int> > near_pairs; //定义特征点匹配对
//两个嵌套for循环表示得到不同的两个待拼接图像
for (int i = 0; i < num_images - 1; ++i)
for (int j = i + 1; j < num_images; ++j)
//如果这两幅图像都得到了特征点，并且它们需要匹配，则把这两幅图像组成一个匹配图像对，放入near_pairs中
if (features[i].keypoints.size() > 0 && features[j].keypoints.size() > 0 && mask_(i, j))
near_pairs.push_back(make_pair(i, j));
//重新定义pairwise_matches的大小
pairwise_matches.resize(num_images * num_images);
//实例化MatchPairsBody结构
MatchPairsBody body(*this, features, pairwise_matches, near_pairs);
//如果并行处理可靠，则并行处理匹配图像对的特征点匹配，否则串行处理
if (is_thread_safe_)
parallel_for_(Range(0, static_cast<int>(near_pairs.size())), body);
else
body(Range(0, static_cast<int>(near_pairs.size())));
LOGLN_CHAT("");
MatchPairsBody结构：
struct MatchPairsBody : ParallelLoopBody
//构造函数
MatchPairsBody(FeaturesMatcher &_matcher, const vector<ImageFeatures> &_features,
vector<MatchesInfo> &_pairwise_matches, vector<pair<int,int> > &_near_pairs)
: matcher(_matcher), features(_features),
pairwise_matches(_pairwise_matches), near_pairs(_near_pairs)
//重载( )运算符，完成特征点匹配
void operator ()(const Range &r) const
const int num_images = static_cast<int>(features.size()); //待拼接的图像数量
for (int i = r.start; i < r.end; ++i) //遍历匹配对
int from = near_pairs[i].first; //提取出当前匹配对的第一幅图像
int to = near_pairs[i].second; //提取出当前匹配对的第二幅图像
int pair_idx = from*num_images + to; //得到当前匹配对的索引
//执行FeaturesMatcher类的第一个重载( )运算符，即调用该类的match函数
matcher(features[from], features[to], pairwise_matches[pair_idx]);
//得到两个匹配对的图像索引
pairwise_matches[pair_idx].src_img_idx = from;
pairwise_matches[pair_idx].dst_img_idx = to;
//另一种索引的形式，因为第i幅图像与第j幅图像匹配，也等于第j幅图像与第i幅图像匹配
size_t dual_pair_idx = to*num_images + from;
pairwise_matches[dual_pair_idx] = pairwise_matches[pair_idx];
pairwise_matches[dual_pair_idx].src_img_idx = to;
pairwise_matches[dual_pair_idx].dst_img_idx = from;
//把第一种索引形式下得到的单应矩阵H复制给第二种索引形式下的H
if (!pairwise_matches[pair_idx].H.empty())
pairwise_matches[dual_pair_idx].H = pairwise_matches[pair_idx].H.inv();
//交换两个匹配下的索引值
for (size_t j = 0; j < pairwise_matches[dual_pair_idx].matches.size(); ++j)
std::swap(pairwise_matches[dual_pair_idx].matches[j].queryIdx,
pairwise_matches[dual_pair_idx].matches[j].trainIdx);
LOG(".");
FeaturesMatcher &matcher;
const vector<ImageFeatures> &features;
vector<MatchesInfo> &pairwise_matches;
vector<pair<int,int> > &near_pairs;
private:
void operator =(const MatchPairsBody&);
;
BestOf2NearestMatcher是FeaturesMatcher的一个子类，它的作用是应用2-NN方法（即找到两个最近邻的特征点）实现特征匹配，这里我们主要介绍它的构造函数和match函数。
BestOf2NearestMatcher类的构造函数：
BestOf2NearestMatcher::BestOf2NearestMatcher(bool try_use_gpu, float match_conf, int num_matches_thresh1, int num_matches_thresh2)
//try_use_gpu表示是否使用GPU，缺省值为false
//match_conf用来衡量两个最近邻的特征点的相似程度，即式1中的ρ，该值在0和1之间，越接近1，两个特征点就越不相近，缺省值为0.3
//num_matches_thresh1表示两幅图像匹配点对的数量阈值，小于该值，则说明两幅图像没有重叠的地方，无需拼接，缺省值为6
//num_matches_thresh2表示内点的阈值，小于该值，说明再用内点来计算单应矩阵就不再有意义，缺省值为6
#if defined(HAVE_OPENCV_GPU) && !defined(DYNAMIC_CUDA_SUPPORT)
if (try_use_gpu && getCudaEnabledDeviceCount() > 0)
impl_ = new GpuMatcher(match_conf);
else
#else
(void)try_use_gpu; //清空该变量
#endif
//实例化CpuMatcher类，CpuMatcher也是FeaturesMatcher类的一个子类，它主要负责特征匹配，而不负责单应矩阵的计算
impl_ = new CpuMatcher(match_conf);
is_thread_safe_ = impl_->isThreadSafe(); //赋值，表示可以并行处理图像匹配
num_matches_thresh1_ = num_matches_thresh1; //阈值赋值
num_matches_thresh2_ = num_matches_thresh2; //阈值赋值
BestOf2NearestMatcher类的match函数：
void BestOf2NearestMatcher::match(const ImageFeatures &features1, const ImageFeatures &features2,
MatchesInfo &matches_info)
//features1和features2分别表示待匹配的两幅图像的特征
//matches_info表示匹配信息
//调用CpuMatcher类中的match函数，得到匹配信息matches_info，该函数在后面会详细介绍
(*impl_)(features1, features2, matches_info);
// Check if it makes sense to find homography
//判断两幅图像的匹配点对的数量是否达到了设置的阈值，如果小于该阈值，说明两幅图像没有重叠的地方，无需再进行拼接
if (matches_info.matches.size() < static_cast<size_t>(num_matches_thresh1_))
return;
// Construct point-point correspondences for homography estimation
//定义两个矩阵，用于保存两幅图像的匹配点对的坐标
Mat src_points(1, static_cast<int>(matches_info.matches.size()), CV_32FC2);
Mat dst_points(1, static_cast<int>(matches_info.matches.size()), CV_32FC2);
//遍历所有匹配点对，得到匹配点对的特征点坐标
for (size_t i = 0; i < matches_info.matches.size(); ++i)
const DMatch& m = matches_info.matches[i];
//得到第一幅图像的当前匹配点对的特征点坐标
Point2f p = features1.keypoints[m.queryIdx].pt;
//以图像的中心处为坐标原点，得到此时的特征点坐标，因为默认情况下是以图像的左上角为坐标原点的
p.x -= features1.img_size.width * 0.5f;
p.y -= features1.img_size.height * 0.5f;
src_points.at<Point2f>(0, static_cast<int>(i)) = p; //特征点坐标赋值
//得到第二幅图像的当前匹配点对的特征点坐标
p = features2.keypoints[m.trainIdx].pt;
//以图像的中心处为坐标原点，得到此时的特征点坐标，因为默认情况下是以图像的左上角为坐标原点的
p.x -= features2.img_size.width * 0.5f;
p.y -= features2.img_size.height * 0.5f;
dst_points.at<Point2f>(0, static_cast<int>(i)) = p; //特征点坐标赋值
// Find pair-wise motion
//利用所有的匹配点对得到单应矩阵，findHomography函数在后面有详细的讲解，src_points和dst_points分别表示两幅图像的特征点，它们是匹配点对的关系，matches_info.inliers_mask表示内点的掩码，即哪些特征点属于内点，CV_RANSAC表示使用RANSAC的方法来得到单应矩阵
matches_info.H = findHomography(src_points, dst_points, matches_info.inliers_mask, CV_RANSAC);
//计算单应矩阵的行列式的值，如果小于一个很小的值，则直接退出该函数
if (std::abs(determinant(matches_info.H)) < numeric_limits<double>::epsilon())
return;
// Find number of inliers
matches_info.num_inliers = 0; //匹配点对的内点数先清零
//由内点掩码得到内点数
for (size_t i = 0; i < matches_info.inliers_mask.size(); ++i)
if (matches_info.inliers_mask[i])
matches_info.num_inliers++;
// These coeffs are from paper M. Brown and D. Lowe. "Automatic Panoramic Image Stitching
// using Invariant Features"
//计算匹配置信度c，式23
matches_info.confidence = matches_info.num_inliers / (8 + 0.3 * matches_info.matches.size());
// Set zero confidence to remove matches between too close images, as they don't provide
// additional information anyway. The threshold was set experimentally.
//如果匹配置信度太大（大于3，3为实验数据），则认为这两幅图像十分接近，可以被看成是一幅图像，因此无需匹配，并要把置信度重新赋值为0
matches_info.confidence = matches_info.confidence > 3. ? 0. : matches_info.confidence;
// Check if we should try to refine motion
//判断内点数是否小于阈值，如果小于，则直接退出
if (matches_info.num_inliers < num_matches_thresh2_)
return;
// Construct point-point correspondences for inliers only
//重新创建src_points和dst_points这两个矩阵，用来存储内点
src_points.create(1, matches_info.num_inliers, CV_32FC2);
dst_points.create(1, matches_info.num_inliers, CV_32FC2);
int inlier_idx = 0; //表示内点索引
for (size_t i = 0; i < matches_info.matches.size(); ++i) //遍历匹配点对，得到内点
if (!matches_info.inliers_mask[i]) //不是内点
continue;
const DMatch& m = matches_info.matches[i]; //赋值
Point2f p = features1.keypoints[m.queryIdx].pt; //第一幅图像的内点坐标
p.x -= features1.img_size.width * 0.5f; //把坐标原点移至图像中心处
p.y -= features1.img_size.height * 0.5f;
src_points.at<Point2f>(0, inlier_idx) = p; //赋值
p = features2.keypoints[m.trainIdx].pt; //第二幅图像的内点坐标
p.x -= features2.img_size.width * 0.5f; //把坐标原点移至图像中心处
p.y -= features2.img_size.height * 0.5f;
dst_points.at<Point2f>(0, inlier_idx) = p; //赋值
inlier_idx++; //索引计数
// Rerun motion estimation on inliers only
//最后再用内点来计算单应矩阵，其实在上次调用findHomography函数时，findHomography函数内部已实现了用内点计算单应矩阵，这里又执行了一遍是为了增强鲁棒性
matches_info.H = findHomography(src_points, dst_points, CV_RANSAC);
CpuMatcher类中的match函数主要负责特征匹配：
void CpuMatcher::match(const ImageFeatures &features1, const ImageFeatures &features2, MatchesInfo& matches_info)
//确保两幅图像的特征描述符的类型一致，以及第二幅图像的描述符的格式正确
CV_Assert(features1.descriptors.type() == features2.descriptors.type());
CV_Assert(features2.descriptors.depth() == CV_8U || features2.descriptors.depth() == CV_32F);
#ifdef HAVE_TEGRA_OPTIMIZATION
if (tegra::match2nearest(features1, features2, matches_info, match_conf_))
return;
#endif
matches_info.matches.clear(); //清空
//定义K-D树形式的索引
Ptr<flann::IndexParams> indexParams = new flann::KDTreeIndexParams();
//定义搜索参数
Ptr<flann::SearchParams> searchParams = new flann::SearchParams();
if (features2.descriptors.depth() == CV_8U)
indexParams->setAlgorithm(cvflann::FLANN_INDEX_LSH);
searchParams->setAlgorithm(cvflann::FLANN_INDEX_LSH);
//使用FLANN方法匹配，定义matcher变量
FlannBasedMatcher matcher(indexParams, searchParams);
vector< vector<DMatch> > pair_matches; //表示邻域特征点
MatchesSet matches; //表示匹配点对
// Find 1->2 matches
//在第二幅图像中，找到与第一幅图像的特征点最相近的两个特征点
matcher.knnMatch(features1.descriptors, features2.descriptors, pair_matches, 2);
for (size_t i = 0; i < pair_matches.size(); ++i) //遍历这两次匹配结果
//如果相近的特征点少于2个，则继续下个匹配
if (pair_matches[i].size() < 2)
continue;
//得到两个最相近的特征点
const DMatch& m0 = pair_matches[i][0];
const DMatch& m1 = pair_matches[i][1];
//比较这两个最相近的特征点的相似程度，当满足一定条件时（用match_conf_变量来衡量），才能认为匹配成功
if (m0.distance < (1.f - match_conf_) * m1.distance) //式1
//把匹配点对分别保存在matches_info和matches中
matches_info.matches.push_back(m0);
matches.insert(make_pair(m0.queryIdx, m0.trainIdx));
LOG("\\n1->2 matches: " << matches_info.matches.size() << endl);
// Find 2->1 matches
pair_matches.clear(); //变量清零
//在第一幅图像中，找到与第二幅图像的特征点最相近的两个特征点
matcher.knnMatch(features2.descriptors, features1.descriptors, pair_matches, 2);
for (size_t i = 0; i < pair_matches.size(); ++i) //遍历这两次匹配结果
//如果相近的特征点少于2个，则继续下个匹配
if (pair_matches[i].size() < 2)
continue;
//得到两个最相近的特征点
const DMatch& m0 = pair_matches[i][0];
const DMatch& m1 = pair_matches[i][1];
if (m0.distance < (1.f - match_conf_) * m1.distance) //表明匹配成功，式1
//如果当前的匹配点对还没有被上一次调用knnMatch函数时得到，则需要把这次的匹配点对保存下来
if (matches.find(make_pair(m0.trainIdx, m0.queryIdx)) == matches.end())
matches_info.matches.push_back(DMatch(m0.trainIdx, m0.queryIdx, m0.distance));
LOG("1->2 & 2->1 matches: " << matches_info.matches.size() << endl);
findHomography函数的作用是得到单应矩阵H，它有两种形式，但归根到底都是执行的下面这种形式：
cv::Mat cv::findHomography( InputArray _points1, InputArray _points2,
int method, double ransacReprojThreshold, OutputArray _mask )
//_points1和_points2分别表示两幅图像匹配点对的特征点
//method表示计算单应矩阵的方法
//ransacReprojThreshold表示重映射误差阈值η，该参数仅在RANSAC算法中使用
//_mask表示输出掩码，用以区分内点和外点
//该函数返回单应矩阵
//得到两幅图像匹配点对的特征点矩阵的形式
Mat points1 = _points1.getMat(), points2 = _points2.getMat();
int npoints = points1.checkVector(2); //匹配点对的数量
//确保匹配点对数量大于0，并且两幅图像的匹配点对数量和类型要一致
CV_Assert( npoints >= 0 && points2.checkVector(2) == npoints &&
points1.type() == points2.type());
Mat H(3, 3, CV_64F); //表示单应矩阵
CvMat _pt1 = points1, _pt2 = points2; //赋值
//c_mask表示_mask的另一种形式，p_mask表示c_mask的指针
CvMat matH = H, c_mask, *p_mask = 0;
if( _mask.needed() ) //如果需要掩码_mask
_mask.create(npoints, 1, CV_8U, -1, true); //创建_mask
p_mask = &(c_mask = _mask.getMat()); //赋值
bool ok = cvFindHomography( &_pt1, &_pt2, &matH, method, ransacReprojThreshold, p_mask ) > 0; //调用cvFindHomography函数
if( !ok ) //如果没有得到单应矩阵
H = Scalar(0); //赋值单应矩阵为0矩阵
return H; //返回单应矩阵
具体计算单应矩阵的函数cvFindHomography：
CV_IMPL int
cvFindHomography( const CvMat* objectPoints, const CvMat* imagePoints,
CvMat* __H, int method, double ransacReprojThreshold,
CvMat* mask )
const double confidence = 0.995; //表示式20中的q
const int maxIters = 2000; //初始化RANSAC算法的最大迭代次数
const double defaultRANSACReprojThreshold = 3; //表示重映射误差阈值η的默认值
bool result = false; //表示单应矩阵的计算是否成功
//m和M分别表示imagePoints和objectPoints的齐次坐标下的值，tempMask表示掩码
Ptr<CvMat> m, M, tempMask;
double H[9]; //代表单应矩阵H的向量形式h
CvMat matH = cvMat( 3, 3, CV_64FC1, H ); //表示单应矩阵
int count; //表示特征点的数量
//确保输入的两个特征点是矩阵的形式
CV_Assert( CV_IS_MAT(imagePoints) && CV_IS_MAT(objectPoints) );
count = MAX(imagePoints->cols, imagePoints->rows); //得到特征点的数量
CV_Assert( count >= 4 ); //确保特征点的数量必须不小于4个
//如果输入的重映射误差阈值η不大于0，则重新设置为默认值
if( ransacReprojThreshold <= 0 )
ransacReprojThreshold = defaultRANSACReprojThreshold;
//把特征点imagePoints的直角坐标转换为齐次坐标m
m = cvCreateMat( 1, count, CV_64FC2 );
cvConvertPointsHomogeneous( imagePoints, m );
//把特征点objectPoints的直角坐标转换为齐次坐标M
M = cvCreateMat( 1, count, CV_64FC2 );
cvConvertPointsHomogeneous( objectPoints, M );
if( mask ) //如果定义了掩码mask，则必须确保该变量的格式正确
CV_Assert( CV_IS_MASK_ARR(mask) && CV_IS_MAT_CONT(mask->type) &&
(mask->rows == 1 || mask->cols == 1) &&
mask->rows*mask->cols == count );
//创建tempMask，并赋值为1
if( mask || count > 4 )
tempMask = cvCreateMat( 1, count, CV_8U );
if( !tempMask.empty() )
cvSet( tempMask, cvScalarAll(1.) );
//定义CvHomographyEstimator类变量，表示用4个匹配点对估计计算单应矩阵
CvHomographyEstimator estimator(4);
//基于method值的不同，应用不同的算法来计算单应矩阵，在这里，我们用的是RANSAC算法，所以调用的是runRANSAC函数，该函数会在后面给出详细的介绍
if( count == 4 )
method = 0;
if( method == CV_LMEDS ) //最小中值法
result = estimator.runLMeDS( M, m, &matH, tempMask, confidence, maxIters );
else if( method == CV_RANSAC ) //RANSAC算法
result = estimator.runRANSAC( M, m, &matH, tempMask, ransacReprojThreshold, confidence, maxIters);
else //最小二乘法
result = estimator.runKernel( M, m, &matH ) > 0;
//如果应用的是最小中值法或RANSAC算法，并且得到了正确的单应矩阵，则需要应用所有的内点得到最终的单应矩阵
if( result && count > 4 )
//在M中提取出内点
icvCompressPoints( (CvPoint2D64f*)M->data.ptr, tempMask->data.ptr, 1, count );
//在m中提取出内点，并得到内点的数量count
count = icvCompressPoints( (CvPoint2D64f*)m->data.ptr, tempMask->data.ptr, 1, count );
//重新定义m和M的长度，因为前count个元素就是内点
M->cols = m->cols = count;
//如果是RANSAC方法，则再用所有的内点得到最终的单应矩阵matH
if( method == CV_RANSAC )
estimator.runKernel( M, m, &matH );
//应用LM算法计算单应函数，refine函数在后面会给出详细的介绍
estimator.refine( M, m, &matH, 10 );
if( result ) //转换单应矩阵的格式
cvConvert( &matH, __H );
if( mask && tempMask ) //转换内点掩码mask的格式
if( CV_ARE_SIZES_EQ(mask, tempMask) )
cvCopy( tempMask, mask );
else
cvTranspose( tempMask, mask );
return (int)result; //返回
在前面的cvFindHomography函数中，用到了CvHomographyEstimator类，而它是CvModelEstimator2的子类，在该父类中实现了具体的计算单应矩阵的不同算法，在这里我们只介绍runRANSAC函数：
bool CvModelEstimator2::runRANSAC( const CvMat* m1, const CvMat* m2, CvMat* model,
CvMat* mask0, double reprojThreshold,
double confidence, int maxIters )
//m1和m2分别为两幅图像的特征点
//model表示输出得到的单应矩阵
//mask0表示输出的掩码
//reprojThreshold表示重映射误差阈值
//confidence表示式20中的q，该值为0.995
//maxIters表示最大迭代次数
bool result = false; //表示输出标志变量
cv::Ptr<CvMat> mask = cvCloneMat(mask0); //复制
//models分别表示为单应矩阵、重映射误差和掩码
cv::Ptr<CvMat> models, err, tmask;
cv::Ptr<CvMat> ms1, ms2; //表示计算单应矩阵时要应用的特征点矩阵形式
int iter, niters = maxIters; //分别表示迭代索引和最大迭代次数
//count表示特征点的数量，maxGoodCount表示最佳单应矩阵下的内点的数量
int count = m1->rows*m1->cols, maxGoodCount = 0;
//确保m1、m2和mask0的大小一致
CV_Assert( CV_ARE_SIZES_EQ(m1, m2) && CV_ARE_SIZES_EQ(m1, mask) );
//全局变量modelPoints表示计算单应矩阵所需要的特征点的数量，在这里，该值在定义CvHomographyEstimator类时，已通过构造函数被赋值为4
if( count < modelPoints ) //特征点的数量不能小于modelPoints
return false;
//全局变量modelSize和maxBasicSolutions分别表示单应矩阵尺寸大小和分辨率，在这里，这两个值在定义CvHomographyEstimator类时，已通过构造函数分别被默认为cvSize(3,3)和1
//创建models、err和tmask
models = cvCreateMat( modelSize.height*maxBasicSolutions, modelSize.width, CV_64FC1 );
err = cvCreateMat( 1, count, CV_32FC1 );
tmask = cvCreateMat( 1, count, CV_8UC1 );
//创建ms1和ms2
if( count > modelPoints ) //特征点的数量大于modelPoints
ms1 = cvCreateMat( 1, modelPoints, m1->type );
ms2 = cvCreateMat( 1, modelPoints, m2->type );
else //特征点的数量等于modelPoints
niters = 1; //表示只迭代一次
ms1 = cvCloneMat(m1);
ms2 = cvCloneMat(m2);
for( iter = 0; iter < niters; iter++ ) //进入迭代循环
int i, goodCount, nmodels; //goodCount表示内点的数量
//如果特征点的数量大于modelPoints，则需要随机抽取出modelPoints个特征点
if( count > modelPoints )
//分别从m1和m2中经过不大于300次的迭代，抽取出modelPoints个特征点，放入ms1和ms2中，并且要求modelPoints个特征点中任意3点都不能共线
bool found = getSubset( m1, m2, ms1, ms2, 300 );
if( !found ) //如果此次的迭代，没能成功抽取出modelPoints个特征点
if( iter == 0 ) //如果是第0次迭代，则退出该函数
return false;
break; //退出迭代循环
//调用CvHomographyEstimator::runKernel函数，利用最小二乘法计算单应矩阵models，该函数在后面给出详细的介绍，如果执行runKernel时，得到了单应函数，则nmodels为1，否则为0
nmodels = runKernel( ms1, ms2, models );
if( nmodels <= 0 ) //此次迭代没有得到单应矩阵，则进行下次迭代
continue;
//得到了单应矩阵，此循环只执行一次，因为此时nmodels为1
for( i = 0; i < nmodels; i++ )
CvMat model_i;
//把3×3的单应矩阵models转换为1×9的行向量的形式model_i
cvGetRows( models, &model_i, i*modelSize.height, (i+1)*modelSize.height );
//以掩码的形式得到内点，findInliers在后面给出详细的介绍
goodCount = findInliers( m1, m2, &model_i, err, tmask, reprojThreshold );
//如果当前得到内点数量比以前的多，则更新最佳单应矩阵
if( goodCount > MAX(maxGoodCount, modelPoints-1) )
std::swap(tmask, mask); //更新掩码
cvCopy( &model_i, model ); //更新单应矩阵
maxGoodCount = goodCount; //更新最大内点数
//重新计算最大迭代次数niters，后面有详细介绍
niters = cvRANSACUpdateNumIters( confidence,
(double)(count - goodCount)/count, modelPoints, niters );
if( maxGoodCount > 0 ) //得到了单应矩阵，重新赋值掩码
if( mask != mask0 )
cvCopy( mask, mask0 );
result = true; //表示得到了单应矩阵
return result; //函数返回
前面有多个地方调用了runKernel函数，它的本质是利用最小二乘法计算单应矩阵：
int CvHomographyEstimator::runKernel( const CvMat* m1, const CvMat* m2, CvMat* H )
//m1和m2表示匹配点对的特征点
//H表示得到的单应矩阵
int i, count = m1->rows*m1->cols; //count表示特征点的数量
const CvPoint2D64f* M = (const CvPoint2D64f*)m1->data.ptr; //得到矩阵m1的指针
const CvPoint2D64f* m = (const CvPoint2D64f*)m2->data.ptr; //得到矩阵m2的指针
//LtL表示式18中的待分解的矩阵ATA，W表示特征值，V表示特征向量
double LtL[9][9], W[9][1], V[9][9];
//把上面定义的数组转换为矩阵的形式
CvMat _LtL = cvMat( 9, 9, CV_64F, LtL );
CvMat matW = cvMat( 9, 1, CV_64F, W );
CvMat matV = cvMat( 9, 9, CV_64F, V );
CvMat _H0 = cvMat( 3, 3, CV_64F, V[8] ); //表示最后一个特征向量，即为式18的h
CvMat _Htemp = cvMat( 3, 3, CV_64F, V[7] ); //表示临时用到的向量变量
//cM和cm表示位移量，sM和sm表示尺度
CvPoint2D64f cM=0,0, cm=0,0, sM=0,0, sm=0,0;
//按式10计算位移量
for( i = 0; i < count; i++ )
cm.x += m[i].x; cm.y += m[i].y;
cM.x += M[i].x; cM.y += M[i].y;
cm.x /= count; cm.y /= count;
cM.x /= count; cM.y /= count;
//按式11计算坐标尺度
for( i = 0; i < count; i++ )
sm.x += fabs(m[i].x - cm.x);
sm.y += fabs(m[i].y - cm.y);
sM.x += fabs(M[i].x - cM.x);
sM.y += fabs(M[i].y - cM.y);
//式11中的分母值不能太小
if( fabs(sm.x) < DBL_EPSILON || fabs(sm.y) < DBL_EPSILON ||
fabs(sM.x) < DBL_EPSILON || fabs(sM.y) < DBL_EPSILON )
return 0; //函数返回，0表示计算失败
sm.x = count/sm.x; sm.y = count/sm.y;
sM.x = count/sM.x; sM.y = count/sM.y;
double invHnorm[9] = 1./sm.x, 0, cm.x, 0, 1./sm.y, cm.y, 0, 0, 1 ; //式16
double Hnorm2[9] = sM.x, 0, -cM.x*sM.x, 0, sM.y, -cM.y*sM.y, 0, 0, 1 ; //式12中的T
CvMat _invHnorm = cvMat( 3, 3, CV_64FC1, invHnorm ); //矩阵形式
CvMat _Hnorm2 = cvMat( 3, 3, CV_64FC1, Hnorm2 ); //矩阵形式
cvZero( &_LtL ); //_LtL清零
for( i = 0; i < count; i++ ) //遍历所有的匹配点对
double x = (m[i].x - cm.x)*sm.x, y = (m[i].y - cm.y)*sm.y; //表示式14的第一项
double X = (M[i].x - cM.x)*sM.x, Y = (M[i].y - cM.y)*sM.y; //表示式14的第二项
double Lx[] = X, Y, 1, 0, 0, 0, -x*X, -x*Y, -x ; //表示式7中的第一行
double Ly[] = 0, 0, 0, X, Y, 1, -y*X, -y*Y, -y ; //表示式7中的第二行
int j, k;
//因为ATA是对称矩阵，所以这里只需得到该矩阵的右上角元素即可
for( j = 0; j < 9; j++ )
for( k = j; k < 9; k++ )
LtL[j][k] += Lx[j]*Lx[k] + Ly[j]*Ly[k];
//把ATA的右上角元素复制到左下角，构成完整的ATA
cvCompleteSymm( &_LtL );
//cvSVD( &_LtL, &matW, 0, &matV, CV_SVD_MODIFY_A + CV_SVD_V_T );
cvEigenVV( &_LtL, &matV, &matW ); //对ATA进行特征值分解
//下面两个矩阵乘法实现了式15
cvMatMul( &_invHnorm, &_H0, &_Htemp );
cvMatMul( &_Htemp, &_Hnorm2, &_H0 );
//对H进行归一化处理，使h9为1
cvConvertScale( &_H0, H, 1./_H0.data.db[8] );
return 1;
得到内点的函数：
int CvModelEstimator2::findInliers( const CvMat* m1, const CvMat* m2,
const CvMat* model, CvMat* _err,
CvMat* _mask, double threshold )
//m1和m2表示匹配点对的特征点
//model表示单应矩阵H
//_err表示重映射误差
//_mask表示内点掩码，内点是用掩码的方式表示的
//threshold表示重映射误差的阈值η
//count表示特征点的数量，goodCount表示最终得到的内点数量
int i, count = _err->rows*_err->cols, goodCount = 0;
const float* err = _err->data.fl; //表示误差指针
uchar* mask = _mask->data.ptr; //表示掩码指针
//调用子类中的computeReprojError函数，见下面的分析
computeReprojError( m1, m2, model, _err );
threshold *= threshold; //误差阈值的平方
//遍历所有特征点，以掩码的形式记录下误差小于阈值的特征点，即内点，并计数
for( i = 0; i < count; i++ )
goodCount += mask[i] = err[i] <= threshold;
return goodCount; //返回内点数量
计算重映射误差，即式21：
oid CvHomographyEstimator::computeReprojError( const CvMat* m1, const CvMat* m2,
const CvMat* model, CvMat* _err )
//m1和m2为匹配点对
//model表示单应矩阵H
//_err表示所有匹配点对的重映射误差，即式21几何距离的平方
int i, count = m1->rows*m1->cols; //count表示特征点的数量
const CvPoint2D64f* M = (const CvPoint2D64f*)m1->data.ptr; //特征点复制指针
const CvPoint2D64f* m = (const CvPoint2D64f*)m2->data.ptr; //特征点复制指针
const double* H = model->data.db; //单应矩阵复制指针
float* err = _err->data.fl; //误差复制指针
for( i = 0; i < count; i++ ) //遍历所有特征点，计算重映射误差
double ww = 1./(H[6]*M[i].x + H[7]*M[i].y + 1.); //式21中分式的分母部分
double dx = (H[0]*M[i].x + H[1]*M[i].y + H[2])*ww - m[i].x; //式21中x坐标之差
double dy = (H[3]*M[i].x + H[4]*M[i].y + H[5])*ww - m[i].y; //式21中y坐标之差
err[i] = (float)(dx*dx + dy*dy); //得到当前匹配点对的重映射误差
利用LM算法计算单应矩阵H：
bool CvHomographyEstimator::refine( const CvMat* m1, const CvMat* m2, CvMat* model, int maxIters )
//m1和m2分别是匹配点对的内点
//model为输入输出变量，输入表示LM算法的初始化H，输出表示LM算法最终得到的H
//maxIters为LM算法的最大迭代次数
//实例化CvLevMarq类，表示LM算法，CvLevMarq类构造函数的第一个参数表示需要优化变量的数量，因为这里我们要得到H的前8个元素，所以该变量设置为8；CvLevMarq类构造函数的第二个参数这里没有用到，所以该变量设置为0；CvLevMarq类构造函数的第三个参数表示LM算法的迭代终止条件
CvLevMarq solver(8, 0, cvTermCriteria(CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, maxIters, DBL_EPSILON));
int i, j, k, count = m1->rows*m1->cols; //count表示特征点的数量
const CvPoint2D64f* M = (const CvPoint2D64f*)m1->data.ptr; //m1指针复制
const CvPoint2D64f* m = (const CvPoint2D64f*)m2->data.ptr; //m2指针复制
//modelPart和solver.param都表示的是单应矩阵
CvMat modelPart = cvMat( solver.param->rows, solver.param->cols, model->type, model->data.ptr );
cvCopy( &modelPart, solver.param ); //复制，初始化用于LM算法的单应矩阵
for(;;) //死循环
const CvMat* _param = 0; //_param表示单应矩阵
CvMat *_JtJ = 0, *_JtErr = 0; //_JtJ表示式28中的JTJ，_JtErr表示式28中的JTe
double* _errNorm = 0; //_errNorm表示式24的误差指标函数
//调用updateAlt函数，由式27和式28计算更新迭代后单应矩阵_param
if( !solver.updateAlt( _param, _JtJ, _JtErr, _errNorm ))
break; //满足迭代终止条件，则退出死循环
//遍历所有内点，计算更新_JtJ、_JtErr和_errNorm
for( i = 0; i < count; i++ )
const double* h = _param->data.db; //单应矩阵赋值
double Mx = M[i].x, My = M[i].y; //得到m1的坐标
double ww = h[6]*Mx + h[7]*My + 1.; //得到式30中分母部分
ww = fabs(ww) > DBL_EPSILON ? 1./ww : 0; //倒数
//计算式25中的横、纵坐标的分式部分
double _xi = (h[0]*Mx + h[1]*My + h[2])*ww;
double _yi = (h[3]*Mx + h[4]*My + h[5])*ww;
double err[] = _xi - m[i].x, _yi - m[i].y ; //式25
if( _JtJ || _JtErr )
double J[][8] = //式30
Mx*ww, My*ww, ww, 0, 0, 0, -Mx*ww*_xi, -My*ww*_xi ,
0, 0, 0, Mx*ww, My*ww, ww, -Mx*ww*_yi, -My*ww*_yi
;
//计算式28中的JTJ和JTe
for( j = 0; j < 8; j++ )
for( k = j; k < 8; k++ )
_JtJ->data.db[j*8+k] += J[0][j]*J[0][k] + J[1][j]*J[1][k];
_JtErr->data.db[j] += J[0][j]*err[0] + J[1][j]*err[1];
if( _errNorm ) //计算式24
*_errNorm += err[0]*err[0] + err[1]*err[1];
cvCopy( solver.param, &modelPart ); //复制单应矩阵
return true;
更新RANSAC迭代次数，即计算式20：
CV_IMPL int
cvRANSACUpdateNumIters( double p, double ep,
int model_points, int max_iters )
//p表示式20中的q
//ep表示式20中的ε
//model_points表示单应矩阵所需要的匹配点对数，这里为4
//max_iters表示迭代的次数
//该函数返回更新后的迭代次数N，即式20的结果
if( model_points <= 0 ) //这里model_points是等于4的
CV_Error( CV_StsOutOfRange, "the number of model points should be positive" );
//确保p和ep都在0和1之间
p = MAX(p, 0.);
p = MIN(p, 1.);
ep = MAX(ep, 0.);
ep = MIN(ep, 1.);
// avoid inf's & nan's
double num = MAX(1. - p, DBL_MIN); //式20中分子log里面的部分
double denom = 1. - pow(1. - ep,model_points); //式20中分母log里面的部分
if( denom < DBL_MIN ) //分母不能太小
return 0;
num = log(num); //式20的分子
denom = log(denom); //式20的分母
//计算式20，更新迭代次数N
return denom >= 0 || -num >= max_iters*(-denom) ?
max_iters : cvRound(num/denom);
2.3 应用
下面我们给出用拼接算法中的匹配方法进行特征匹配的程序：
#include "opencv2/core/core.hpp"
#include "highgui.h"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/features2d/features2d.hpp"
#include "opencv2/nonfree/nonfree.hpp"
#include "opencv2/legacy/legacy.hpp"
#include "opencv2/stitching/detail/autocalib.hpp"
#include "opencv2/stitching/detail/blenders.hpp"
#include "opencv2/stitching/detail/camera.hpp"
#include "opencv2/stitching/detail/exposure_compensate.hpp"
#include "opencv2/stitching/detail/matchers.hpp"
#include "opencv2/stitching/detail/motion_estimators.hpp"
#include "opencv2/stitching/detail/seam_finders.hpp"
#include "opencv2/stitching/detail/util.hpp"
#include "opencv2/stitching/detail/warpers.hpp"
#include "opencv2/stitching/warpers.hpp"
#include <iostream>
#include <fstream>
#include <string>
#include <iomanip>
using namespace cv;
using namespace std;
using namespace detail;
int main(int argc, char** argv)
vector<Mat> imgs; //表示待拼接的图像矢量队列
Mat img = imread("1.jpg"); //读取两幅图像，并存入队列
imgs.push_back(img);
img = imread("2.jpg");
imgs.push_back(img);
Ptr<FeaturesFinder> finder; //特征检测
finder = new SurfFeaturesFinder();
vector<ImageFeatures> features(2);
(*finder)(imgs[0], features[0]);
(*finder)(imgs[1], features[1]);
vector<MatchesInfo> pairwise_matches; //特征匹配
BestOf2NearestMatcher matcher(false, 0.3f, 6, 6); //定义特征匹配器，2NN方法
matcher(features, pairwise_matches); //进行特征匹配
Mat dispimg; //两幅图像合并成一幅图像显示
dispimg.create(Size(imgs[0].cols+imgs[1].cols, max(imgs[1].rows,imgs[1].rows)), CV_8UC3);
Mat imgROI = dispimg(Rect(0, 0, (int)(imgs[0].cols), (int)(imgs[0].rows)));
resize(imgs[0], imgROI, Size((int)(imgs[0].cols), (int)(imgs[0].rows)));
imgROI = dispimg(Rect((int)(imgs[0].cols), 0, (int)(imgs[1].cols), (int)(imgs[1].rows)));
resize(imgs[1], imgROI, Size((int)(imgs[1].cols), (int)(imgs[1].rows)));
Point2f p1, p2; //分别表示两幅图像内的匹配点对
int j=0;
for (size_t i = 0; i < pairwise_matches[1].matches.size(); ++i) //遍历匹配点对
if (!pairwise_matches[1].inliers_mask[i]) //不是内点，则继续下一次循环
continue;
const DMatch& m = pairwise_matches[1].matches[i]; //得到内点的匹配点对
p1 = features[0].keypoints[m.queryIdx].pt;
p2 = features[1].keypoints[m.trainIdx].pt;
p2.x += features[0].img_size.width; //p2在合并图像上的坐标
line(dispimg, p1, p2, Scalar(0,0,255), 1, CV_AA); //画直线
if(j++==10) //内点数量较多，我们只显示10个
break;
//在终端显示内点数量和单应矩阵
cout<<"内点数量："<<endl;
cout<<setw(10)<<pairwise_matches[1].matches.size()<<endl<<endl;
const double* h = reinterpret_cast<const double*>(pairwise_matches[1].H.data);
cout<<"单应矩阵："<<endl;
cout<<setw(10)<<(int)(h[0]以上是关于Opencv2.4.9源码分析——Stitching的主要内容，如果未能解决你的问题，请参考以下文章
Opencv2.4.9源码分析——Gradient Boosted Trees
Win7下qt5.3.1+opencv2.4.9编译环境的搭建（好多 Opencv2.4.9源码分析的博客）