MATLAB实现矩阵里数值的大小对应颜色的深浅

Posted 2023-04-17

生成如图所示的热点图（设矩阵中的数值越大处对应的条目越亮）。希望大家能帮帮我，谢谢！

MATLAB实现矩阵里数值的大小对应颜色的深浅？数据如果存在矩阵a里面
直接用
imagesc(a)就可以
如果想像图中那样用黑白灰度表示，再加一句
colormap(gray(256))
xy是坐标，z为对应计算出来的值，matlab生成二维图，用颜色表示数值的大小，什么函数能实现求举例？
感觉你可以绘制出三维图去surf，设置不显示网格线，然后设置视角为俯视，再加上colorbar应该就能达到你的要求。
figure1=figure（’color’，[1,1,1]）1 图像转为矩阵后，图像大小和矩阵大小是一样的。
2 图像的最小分辨单元是像素，每个图像有m*n个像素，m代表图像的长，n代表图像的宽；那么与图像对应的矩阵就有m行，n列，总共也有m*n个像素单元，(m,n)就代表该像素在图像中的位置，相当于把图像放到坐标系下，m代表横坐标，n代表纵坐标，(m,n)确定一个像素的位置；而(m,n)处的值代表图像中该点的灰度值，灰度值范围0-255。 参考技术A

数据如果存在矩阵a里面

直接用

imagesc(a)就可以

如果想像图中那样用黑白灰度表示，再加一句

colormap(gray(256))

xy是坐标，z为对应计算出来的值，matlab生成二维图，用颜色表示数值的大小，什么函数能实现求举例？

感觉你可以绘制出三维图去surf，设置不显示网格线，然后设置视角为俯视，再加上colorbar应该就能达到你的要求。

figure1=figure（’color’，[1,1,1]）

参考技术B 数据如果存在矩阵a里面
直接用
imagesc(a)就可以
如果想像图中那样用黑白灰度表示，再加一句
colormap(gray(256))追问

哇哦，好神奇！我实现了一个很小的矩阵的图形化热度图表示，我接下来要继续努力完善了。谢谢！非常感谢！我查了好多好多资料，有种蓦然回首，那人却在灯火阑珊处的赶脚~嘿嘿

本回答被提问者和网友采纳 参考技术C 如果数据在矩阵a内，可用heatmap命令生成热图
heatmap(a) 参考技术D 请问，这中马赛克形式的填充图要怎么实现？非常感谢

Matlab数值积分

实验目的：

1.熟悉Matlab矩阵操作

2.用Matlab实现求积公式：梯形，辛普森，复合梯形，复合辛普森等算法

3.学会数值积分有关应用

实验要求：

1.掌握梯形和辛普森算法

2.掌握复合梯形和复合辛普森算法

3.掌握判断迭代停止的手段

实验内容：

1.矩阵的四则运算、幂运算；矩阵元素的查找、排序、求和、求积差分。

2.用Matlab实现求积公式：梯形，辛普森，复合梯形，复合辛普森等算法

3.学会数值积分有关应用

（补充2，不在实验过程中展示）

实验步骤：

　　1.矩阵的四则运算，进行加减法的前提是参与运算的两个矩阵或多个矩阵必须具有相同的行数和列数；或者其中有一个或多个矩阵为标量。其加减法定义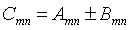：，当其中含有标量x时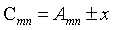，，且矩阵的加法运算满足“交换律”、“结合律”、“存在零元”、“存在负元”的运算律。矩阵加减法示例：

　　

 

 

 　　

 

 

 　　

 

 

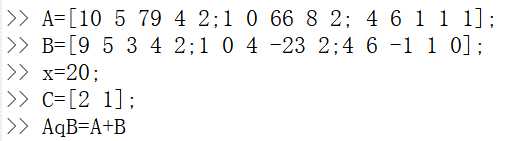
 　　数与矩阵到乘法、矩阵与矩阵的乘法、矩阵的除法。

 　　C的元素就是用书x乘矩阵A对应的元素而得到，数与矩阵的乘法满足下列运算律：， ， ，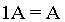 

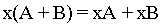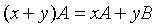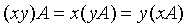
 　　数乘示例：

　　

 

 

 　　A为m*h矩阵，B为h*n矩阵，则两矩阵的乘积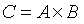为一个矩阵，且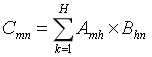且满足“结合律”、“左分配律”、“右分配律”、“单位矩阵的存在性”。矩阵乘法示例：

 

　　

 

 

 　　矩阵的除法是乘法的逆运算，左除“”和右除“/”。若A和B是标量，A/B和BA等价。对一般的二维矩阵A和B，当进行AB运算时，要求A的行数与B的行数相等；当进行A/B运算时，要求A到列数与B的列数相等。矩阵除法示例：

 

 　　

 

 

 　　矩阵的幂运算，当矩阵A为方阵是可进行矩阵的幂运算，其定义为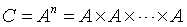：方阵幂运算示例：

 

 

 

　　

 

 

 　　矩阵元素的查找，函数find()的作用是进行矩阵元素的查找，它通常与干洗函数和逻辑运算相结合。语法格式：ind=find(X):该函数查找矩阵X中的非零元素，返回这些元素的单下标；[row,col]=find(X,...):该函数查找矩阵X中的非零元素，函数返回这些元素的双下标i和j。

　　矩阵元素的排序，函数sort()的作用是按升序排序，排序后的矩阵和眼函数矩阵位数一致，语法：B=sort(A):该函数对矩阵A进行升序排序，A可为矩阵或向量；B=sort(A,dim)：当dim=1时矩阵A按列升序，当dim=2时矩阵按行升序；B=sort(...,mode):该函数按mode指定的方式排序（ascend升序，descend降序）。

　　矩阵元素的求和、求积和差分。函数sum()和cumsum()的作用是对矩阵元素求和，函数prod()和cumprod()的作用是对矩阵元素求积，函数diff()的作用计算矩阵的差分示例：

　　

 

 

 

 

 

 

 

 

 

 

 

 

 

 

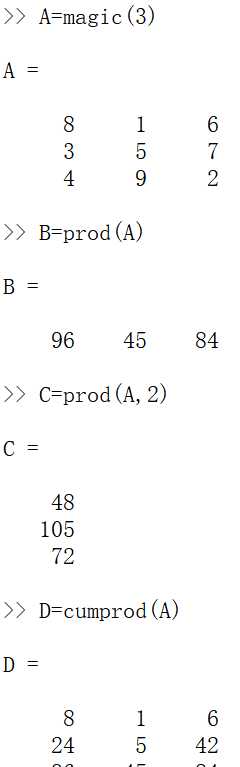
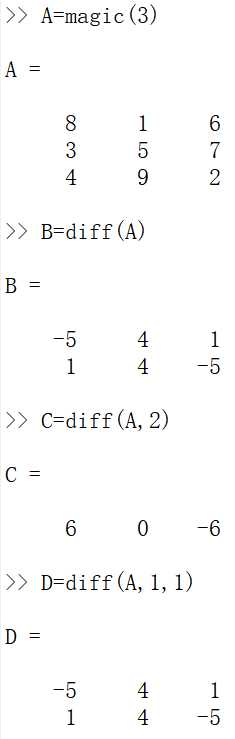
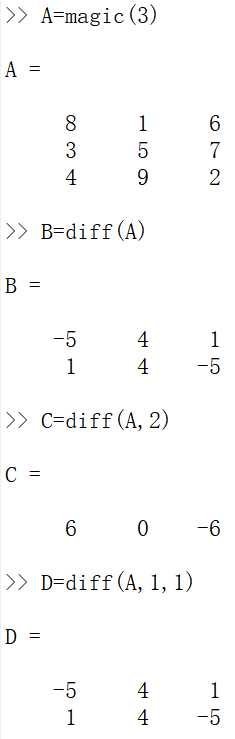
　　2.求积公式，梯形公式示例：

　　

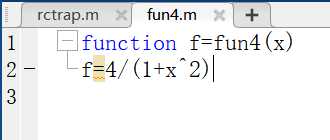
　　梯形求积代码：

 1 function t=rctrap(fun,a,b,n)
 2 %复化梯形公式
 3 %n等分
 4 %a,b区间的左右端点
 5 h=(b-a)/n;
 6 t=0;
 7 for i=1:n-1
 8       t=t+h*feval(fun,i*h+a);
 9 end
10 t=t+0.5*h*(feval(fun,a+eps)+feval(fun,b))

rctrap

　　运行部分截图：

　　 

 

　　辛普森求积代码：

 1 function s=sptrap(fun,a,b,n)
 2 % n，对应的等分点为2n
 3 h=(b-a)/(2*n);
 4 s=0;
 5 for i=1:n
 6 s=s+feval(fun,(2*i-1)*h+a)*4;
 7 end
 8 for i=1:n-1    
 9 s=s+feval(fun,(2*i)*h+a)*2;
10 end
11 s=s+feval(fun,a+eps)+feval(fun,b);
12 s=s*h/3

sptrap

　　运行部分截图：

　　

　　根据梯形公式和估计误差公式编写程序计算积分，分别取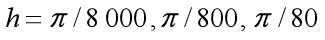，用复合梯形公式计算定积分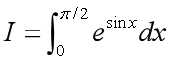并与精确值比较.然后观察 对计算结果的有效数字和绝对误差的影响.

1 h=pi/8000;a=0;b=pi/2;x=a:h:b;n=length(x), y=exp(sin(x));
2 z1=(y(1)+y(n))*h/2; z2=sum(y(2:n-1))*h; z8000=z1+z2,
3 syms t
4 f=exp(sin(t)); intf=int(f,t,a,b), Fs=double(intf),
5 Juewucha8000=abs(z8000-Fs)

Untitled12

　　运行部分示例：

 　　

 

 　　用复合梯形公式计算定积分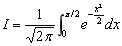，并与精确值比较.然后观察 对计算结果的有效数字和绝对误差的影响.

 

　　

 

 　　代码：

 1 function T=rctrap1(fun1,a,b,m)
 2 n=1;h=b-a; T=zeros(1,m+1); x=a; T(1)=h*(feval(fun1,a)+feval(fun1,b))/2;
 3 for i=1:m 
 4            h=h/2; n=2*n; s=0;
 5           for k=1:n/2
 6            x=a+h*(2*k-1); s=s+feval(fun1,x);
 7 end
 8 T(i+1)=T(i)/2+h*s;
 9 end
10 T=T(1:m);

rctrap1

　　运行：

 

 　　

　　用复合辛普森公式计算定积分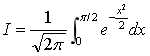取n=20001个等距节点，并与精确值比较.然后再取n=13，观察 n对误差的影响.解 由n=2m+1=20001,得m=10000.根据辛普森公式编写并输入下面的程序。代码：

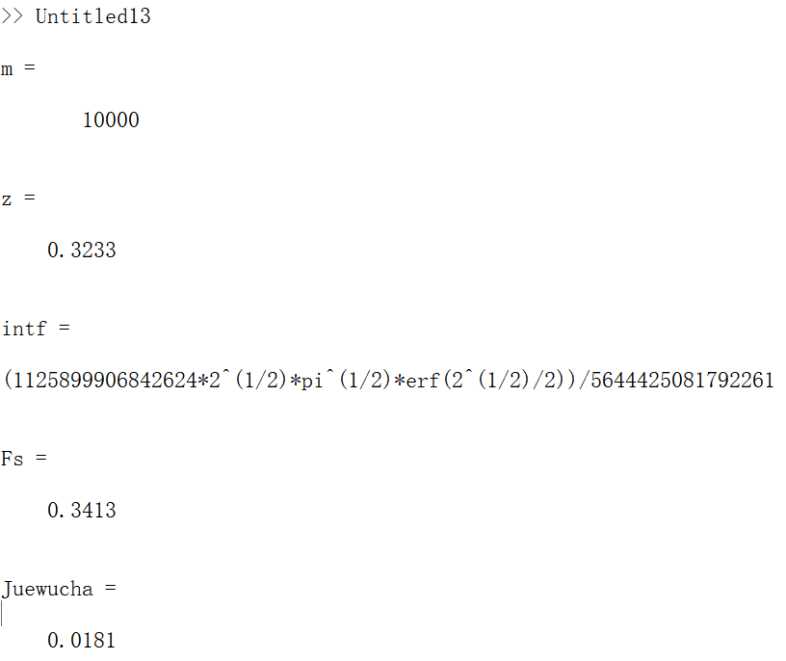
1 a=0;b=1;m=10000
2 m=6; h=(b-a)/(2*m); x=a:h:b; 
3 y=exp((-x.^2)./2)./(sqrt(2*pi));
4 z1=y(1)+y(2*m+1); z2=2*sum(y(2:2:2*m)); 
5 z3=4*sum(y(3:2:2*m));
6 z=(z1+z2+z3)*h/3, syms t,f=exp((-t^2)/2)/(sqrt(2*pi));
7 intf=int(f,t,a,b), Fs=double(intf), Juewucha=abs(z-Fs)

Untitled13

　　运行：

　　

 

 　　复合辛普森数值积分的MATLAB程序comsimpson（fun,a,b,n)。用comsimpson.m和quad.m分别计算定积分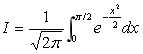取精度为10e-4，并与精确值比较.。代码：

 

　　

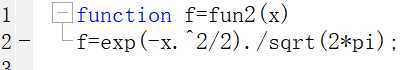
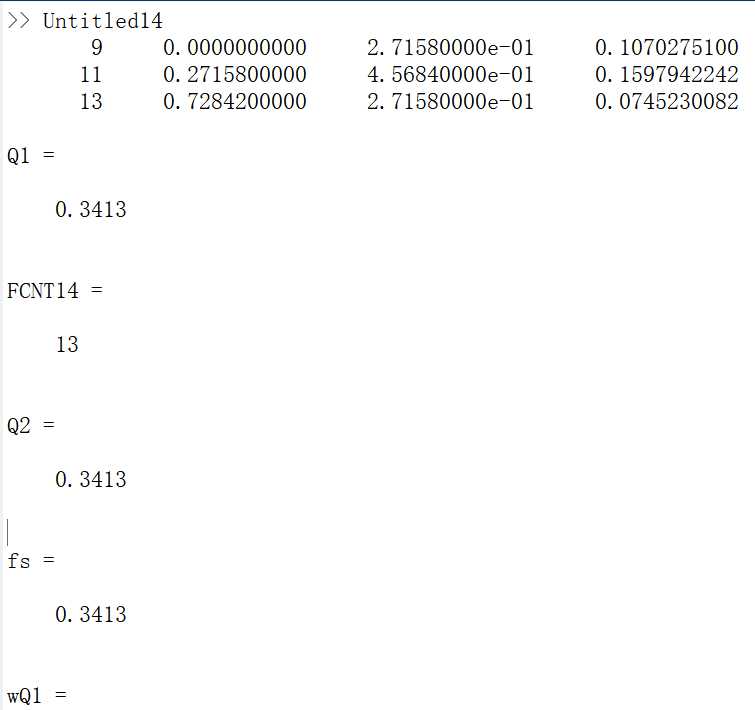
1 [Q1,FCNT14] = quad(@fun2,0,1,1.e-4,3),
2 Q2 =comsimpson (@fun2,0,1,10000)
3 syms x
4 fi=int(exp( (-x^2)/2)/(sqrt(2*pi)),x,0, 1);
5 fs=double(fi)
6 wQ1= double (abs(fi-Q1)), wQ2= double (abs(fi-Q2))

Untitled14

　　

 

 　　运行：

　　

　　

 

 　　

 

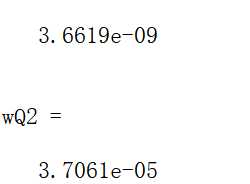
　　3.数值分析的应用。利用复合梯形公式求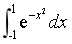。代码：

1 function I=tquad(x,y)
2 n=length(x);m=length(y);
3 if n~=m
4     error(‘向量x,y的长度必须一致‘);
5 end
6 h=(x(n)-x(1))/(n-1);
7 a=[1 2*ones(1,n-2) 1];
8 I=h/2*sum(a.*y);

tquad

 　　运行：

 

 　　

 

 

 

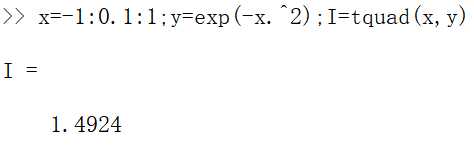
小结：

　　在参考PPT和书本的MATLAB编程之后，感觉解决问题使用计算机的方法，就好像使用一种特殊的语言与一堆无机物交流，并通过一些物理的方法使它回应我们。解数学题的编程的关键，就是熟悉数学规律，并使用该编程语言简洁地表达出来。