LeetCode No.202 快乐数

Posted 2022-08-28 AI算法攻城狮

一、题目描述

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为1，也可能是 无限循环 但始终变不到1。
如果这个过程 结果为1，那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：
输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：
输入：n = 2
输出：false

提示：
1 <= n <= 2^31 - 1

二、解题思路

用哈希集合检测循环
我们可以先举几个例子。我们从 7 开始。则下一个数字是 49（因为 7^2=49），然后下一个数字是 97（因为 4^2+9^2=97）。我们可以不断重复该的过程，直到我们得到 1。因为我们得到了 1，我们知道 7 是一个快乐数，函数应该返回 true。

再举一个例子，让我们从 116开始。通过反复通过平方和计算下一个数字，我们最终得到 58，再继续计算之后，我们又回到 58。由于我们回到了一个已经计算过的数字，可以知道有一个循环，因此不可能达到 1。所以对于 116，函数应该返回 false。

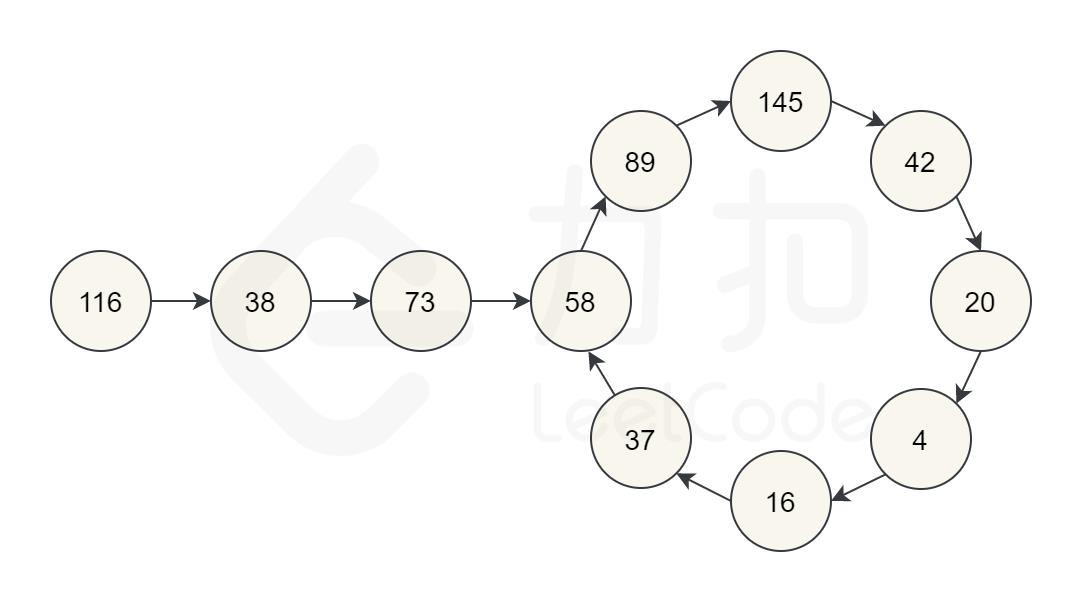
根据我们的探索，我们猜测会有以下三种可能。

最终会得到 1。
最终会进入循环。
值会越来越大，最后接近无穷大。
第三个情况比较难以检测和处理。我们怎么知道它会继续变大，而不是最终得到 1 呢？我们可以仔细想一想，每一位数的最大数字的下一位数是多少。

Digits	Largest	Next
1	9	81
2	99	162
3	999	243
4	9999	324
13	9999999999999	1053

对于 3 位数的数字，它不可能大于 243。这意味着它要么被困在 243 以下的循环内，要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位，直到降到 3 位为止。所以我们知道，最坏的情况下，算法可能会在 243 以下的所有数字上循环，然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去，所以我们排除第三种选择。

即使在代码中你不需要处理第三种情况，你仍然需要理解为什么它永远不会发生，这样你就可以证明为什么你不处理它。

算法

算法分为两部分，我们需要设计和编写代码。

给一个数字 n，它的下一个数字是什么？
按照一系列的数字来判断我们是否进入了一个循环。
第 1 部分我们按照题目的要求做数位分离，求平方和。
第 2 部分可以使用哈希集合完成。每次生成链中的下一个数字时，我们都会检查它是否已经在哈希集合中。

如果它不在哈希集合中，我们应该添加它。
如果它在哈希集合中，这意味着我们处于一个循环中，因此应该返回 false。
我们使用哈希集合而不是向量、列表或数组的原因是因为我们反复检查其中是否存在某数字。检查数字是否在哈希集合中需要 O(1) 的时间，而对于其他数据结构，则需要 O(n)的时间。选择正确的数据结构是解决这些问题的关键部分。

三、代码

class Solution:
    def isHappy(self, n: int) -> bool:
        def get_next(n):
            total_sum=0
            while n>0:
                n, digit = divmod(n, 10)
                total_sum += digit ** 2
                n=n/10
            return total_sum
        seen=set()
        while n!=1 and n not in seen:
            seen.add(n)
            n=get_next(n)
        return n==1

四、复杂度分析

确定这个问题的时间复杂度对于一个「简单」级别的问题来说是一个挑战。如果您对这些问题还不熟悉，可以尝试只计算 getNext(n) 函数的时间复杂度。

时间复杂度：O(243⋅3+logn+loglogn+logloglogn)... = O(logn)。
查找给定数字的下一个值的成本为O(logn)，因为我们正在处理数字中的每位数字，而数字中的位数由logn 给定。
要计算出总的时间复杂度，我们需要仔细考虑循环中有多少个数字，它们有多大。
我们在上面确定，一旦一个数字低于 243，它就不可能回到 243 以上。因此，我们就可以用 243以下最长循环的长度来代替 243，不过，因为常数无论如何都无关紧要，所以我们不会担心它。
对于高于 243的 n，我们需要考虑循环中每个数高于 243的成本。通过数学运算，我们可以证明在最坏的情况下，这些成本将是O(logn)+O(loglogn)+O(logloglogn)...。幸运的是，O(logn)是占主导地位的部分，而其他部分相比之下都很小（总的来说，它们的总和小于logn），所以我们可以忽略它们。
空间复杂度：O(logn)。与时间复杂度密切相关的是衡量我们放入哈希集合中的数字以及它们有多大的指标。对于足够大的 n，大部分空间将由 n 本身占用。我们可以很容易地优化到 O(243⋅3)=O(1)，方法是只保存集合中小于243 的数字，因为对于较高的数字，无论如何都不可能返回到它们。