OpenGL基础仿射变换原理解析

Posted 2023-04-05

参考技术A 仿射变换(Affine Transformation)

仿射变换可以通过一系列的原子变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切（Shear）。

几种典型的仿射变换如下：

将每一点移动到(x+tx, y+ty)，变换矩阵为：

平移变换是一种“刚体变换”，rigid-body transformation，就是不会产生形变的理想物体。
效果：

将每一点的横坐标放大（缩小）至sx倍，纵坐标放大（缩小）至sy倍，变换矩阵为：

变换效果如下：

变换矩阵为：

相当于一个横向剪切与一个纵向剪切的复合

效果：

目标图形围绕原点顺时针旋转theta弧度，变换矩阵为：

效果：

旋转变换，目标图形以(x, y)为轴心顺时针旋转theta弧度，变换矩阵为：

相当于两次平移变换与一次原点旋转变换的复合：

先移动到中心节点，然后旋转，然后再移动回去。

物体变化从最终显示效果的实现基本有两种实现方式:

视觉可以理解为屏幕坐标。是一个虚拟的固定的坐标系。

视图变化是当观察者移动位置时视图相应的发生角度的变换，默认观察者是以z轴负方向观察，当观察沿x轴负方向观察时，实际观察模型的侧面。
一般都是先进行视觉变化，已确定观察的视角，然后进行其它变化。这样更容易理解变化的过程。

是用于操纵模型或某一对象，通过变换改变了其位置，大小或者角度。

模型视图二次元是模型视图两种变换在线性变换管线中的进行组合，成为一个单独的变化矩阵。即模型视图矩阵。

将模型视图变换之后应用到顶点上，这种变换后实际上是确认了视景体和剪裁平面。
对于平行投影来说，视景体是一个四边平行于投影方向，长度无限的四棱柱；
对于透视投影来说，则是以投影中心为顶点的四棱锥。

当以上变换结束后，我们得到了一个场景的二维投影，这时候我们需要将其映射到窗口的某片区域进行显示，还包括颜色缓冲区与窗口像素间的转换。

模型视图矩阵是一个4x4的矩阵，所表示一个变换后的坐标系，模型视图变换就是通过将要变换的顶点和模型变换矩阵相乘得到一个变换后相对于视觉坐标系新的坐标系。
下面是一个模型视图变换的例子

因为计算机只识别单元立方的坐标系,有时候我们需要跳出坐标系进行变换,比如说当我们采用投影变换后得到的非单元立方的坐标系,这时候就要通过模型视图矩阵转型成单位立方矩阵.
下面是一个通过透视投影然后经过模型视图投影矩阵变换的例子

OpenCV图像变换(仿射变换与透视变换)

仿射变换(affine transform)与透视变换(perspective transform)在图像还原、图像局部变化处理方面有重要意义。通常，在2D平面中，仿射变换的应用较多，而在3D平面中，透视变换又有了自己的一席之地。两种变换原理相似，结果也类似，可针对不同的场合使用适当的变换。

仿射变换和透视变换的数学原理不需深究，其计算方法为坐标向量和变换矩阵的乘积，换言之就是矩阵运算。在应用层面，仿射变换是图像基于3个固定顶点的变换，如图所示：

 

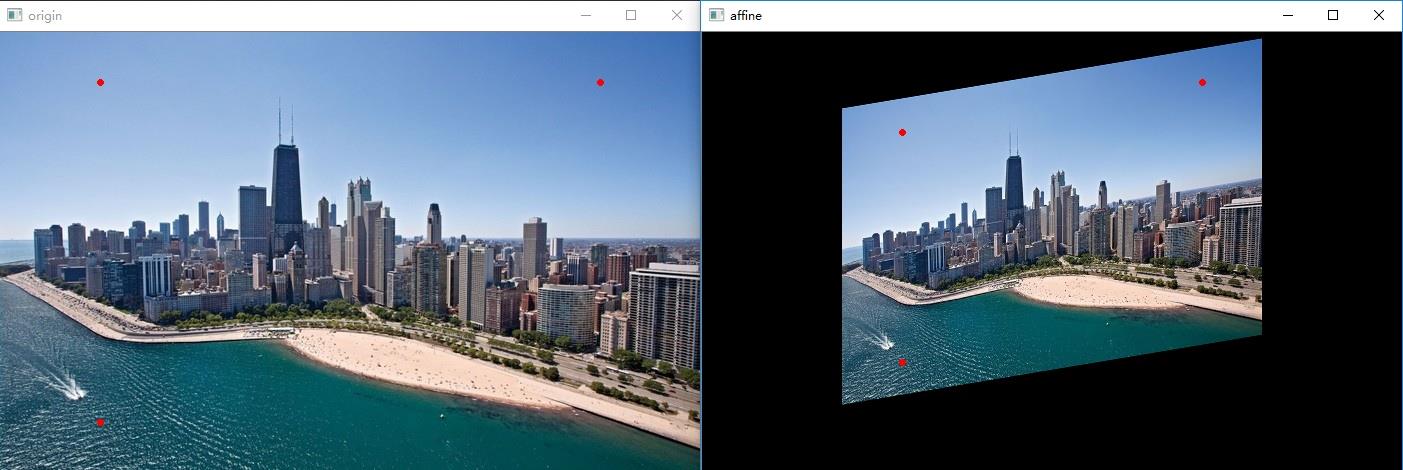
图中红点即为固定顶点，在变换先后固定顶点的像素值不变，图像整体则根据变换规则进行变换

同理，透视变换是图像基于4个固定顶点的变换，如图所示：

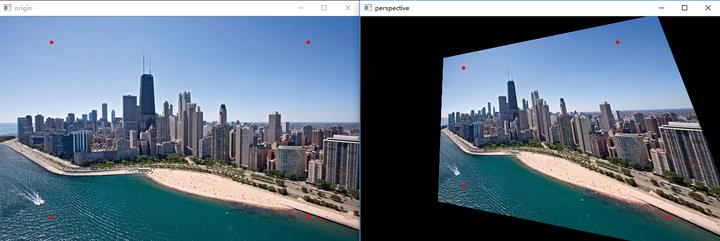
在OpenCV中，仿射变换和透视变换均有封装好的函数，分别为

void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

与

void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

两种变换函数形式完全相同，因此以仿射变换函数为例：

void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

参数InputArray src：输入变换前图像

参数OutputArray dst：输出变换后图像，需要初始化一个空矩阵用来保存结果，不用设定矩阵尺寸

参数InputArray M：变换矩阵，用另一个函数getAffineTransform()计算

参数Size dsize：设置输出图像大小

参数int flags=INTER_LINEAR：设置插值方式，默认方式为线性插值

后两个参数不常用，在此不赘述

关于生成变换矩阵InputArray M的函数getAffineTransform()：

Mat getAffineTransform(const Point2f* src, const Point2f* dst)

参数const Point2f* src：原图的三个固定顶点

参数const Point2f* dst：目标图像的三个固定顶点

返回值：Mat型变换矩阵，可直接用于warpAffine()函数

注意，顶点数组长度超过3个，则会自动以前3个为变换顶点；数组可用Point2f[]或Point2f*表示

示例代码如下：

	//读取原图
	Mat I = imread("..//img.jpg");
	//设置空矩阵用于保存目标图像
	Mat dst;
	//设置原图变换顶点
	Point2f AffinePoints0[3] = { Point2f(100, 50), Point2f(100, 390), Point2f(600, 50) };
	//设置目标图像变换顶点
	Point2f AffinePoints1[3] = { Point2f(200, 100), Point2f(200, 330), Point2f(500, 50) };
	//计算变换矩阵
	Mat Trans = getAffineTransform(AffinePoints0, AffinePoints1);
	//矩阵仿射变换
	warpAffine(I, dst, Trans, Size(I.cols, I.rows));
	//分别显示变换先后图像进行对比
	imshow("src", I);
	imshow("dst", dst);
	waitKey();

同理，透视变换与仿射变换函数类似：

void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

生成变换矩阵函数为：

Mat getPerspectiveTransform(const Point2f* src, const Point2f* dst)

注意，透视变换顶点为4个

两种变换完整代码及结果比较：

#include <iostream>
#include <opencv.hpp>
using namespace std;
using namespace cv;

Mat AffineTrans(Mat src, Point2f* scrPoints, Point2f* dstPoints)
{
	Mat dst;
	Mat Trans = getAffineTransform(scrPoints, dstPoints);
	warpAffine(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);
	return dst;
}

Mat PerspectiveTrans(Mat src, Point2f* scrPoints, Point2f* dstPoints)
{
	Mat dst;
	Mat Trans = getPerspectiveTransform(scrPoints, dstPoints);
	warpPerspective(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);
	return dst;
}

void main()
{
	Mat I = imread("..//img.jpg");	//700*438

	Point2f AffinePoints0[4] = { Point2f(100, 50), Point2f(100, 390), Point2f(600, 50), Point2f(600, 390) };
	Point2f AffinePoints1[4] = { Point2f(200, 100), Point2f(200, 330), Point2f(500, 50), Point2f(600, 390) };
	Mat dst_affine = AffineTrans(I, AffinePoints0, AffinePoints1);
	Mat dst_perspective = PerspectiveTrans(I, AffinePoints0, AffinePoints1);

	for (int i = 0; i < 4; i++)
	{
		circle(I, AffinePoints0[i], 2, Scalar(0, 0, 255), 2);
		circle(dst_affine, AffinePoints1[i], 2, Scalar(0, 0, 255), 2);
		circle(dst_perspective, AffinePoints1[i], 2, Scalar(0, 0, 255), 2);
	}

	imshow("origin", I);
	imshow("affine", dst_affine);
	imshow("perspective", dst_perspective);
	waitKey();
}

结果如图：

 

可以看出，仿射变换以3个点为基准点，即使数组长度为4也仅取前3个点作为基准点；透视变换以4个点为基准点，两种变换结果不相同。应根据实际情况判断使用哪种变换方式更佳

 

转自：https://zhuanlan.zhihu.com/p/24591720