信噪比(dB)换算公式

Posted 2023-03-31 毕业回老家

SNR(dB) = 10*lg(SNR);

1、举例：

0(dB) = 1 =10^0;

10(dB) = 10 =10^1;

20(dB) = 100 =10^2;

30(dB) = 1000 =10^3;

即10*n (dB) = 10^n;

2、转换成dB的意义

压缩坐标轴。

3、图像SNR(dB)与SNR对比

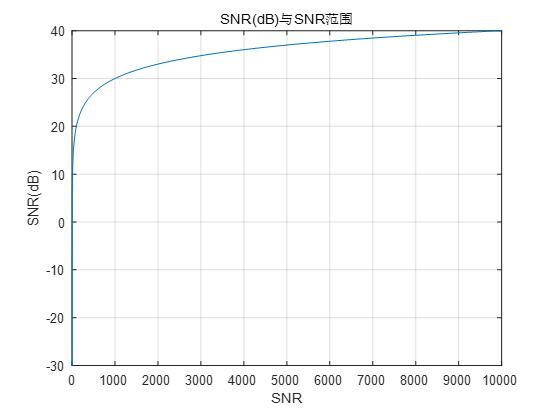
可以看，SNR范围从0-1000，SNR(dB)的最大值只要到40 

4、SNR（dB）作为自变量作图，就不能再用plot了

semilogx(X,Y) 在 x 轴上使用以 10 为底的对数刻度、在 y 轴上使用线性刻度来绘制 x 和 y 坐标。

即横轴单位是(dB)，纵轴是正常的线性坐标。

意义：压缩横轴。

(1)要绘制由线段连接的一组坐标，请将 X 和 Y 指定为相同长度的向量。

(2)要在同一组坐标轴上绘制多组坐标，请将 X 或 Y 中的至少一个指定为矩阵。

在作图时，规定X是用10为底的对数刻度，但是在定义和图中标注X范围时，用的都是正常线性值，只是将线性值用dB的刻度排练而已。

配套函数：

y = logspace(a,b,n) 在 10 的幂 10^a 和 10^b（10 的 N 次幂）之间生成 n 个点。

x = logspace(-1,2);%X的范围：0.1——100
y = x;
semilogx(x,y)&作图，X的坐标是dB
grid on

 5、应用

以提高信道容量的两种方式为例：

5.1增加带宽，带宽增加会提高信道容量，但是不是无极限的，因为带宽增加，噪声功率也增加。当带宽趋于无穷时，信道容量趋于1.44*S/n0

代码：

clc;
clear;
W=logspace(-2,10);%信道带宽范围：0.01—10^10，不用化成dB
S=3;%信号平均功率
N0=0.00001;%单位带宽噪声功率
SNR=S./(N0*W);%信噪比
C=W.*log2(1+SNR);%香农公式
semilogx(W,C),xlabel('W(Hz)'),ylabel('C'),title('带宽对信道容量影响'),grid on;%作图

5.2增加信噪比，无极限，信噪比无穷大，信道容量无穷大。

 代码：

clc;
clear;
SNR = logspace(-4,2);%信噪比范围：不用化成dB
W = 3000;%信道带宽
C=W.*log2(1+SNR);%香农公式
semilogx(SNR,C),xlabel('SNR'),ylabel('C'),title('带宽对信道容量影响'),grid on;%作图

18位采样意义

      面前寻找18位Σ-Δ音频A/D芯片几乎没有，或是早期停产的，基本都是24位的，还有少量16位的。24位十分难以实现，其中之一就是片内外干扰，对于片外干扰容限计算公式如下：

分辨电压 = (基准电压 / 采样位数) * 换算单位(微伏)

多数24位音频采样A/D芯片工作电压不高，但输入端故意拉宽电压，且采用低阻差分方式，以提高信噪比。大多基准电压为2Vrms，要换算为峰峰值，公式为：

峰峰系数（peak-to-peak）= 2√2 V  (≈2.828 V)。

峰峰电压 = 有效值 * 峰峰系数，峰峰基准电压为 = 2V * 2.828 = 5.656V，也就是输入端差分范围。

24位分辨电压 = (基准电压 / 采样位数) * 换算单位(微伏) = (5.656V / 2^24) * 10^6 = 0.33712uV，高级高压摆中速运放窄带宽内峰峰噪音不少于数微伏，噪音已严重超过分辨率。就是无线话筒，也要有线进入线路才能采样，对传输信号屏蔽，也是有限的。还有开关电源顽固性的干扰是无法克服的。这仅仅是对输入噪声容限的影响。实现起来十分困难。对于18位计算公式如下：

18位分辨电压 = (5.656V / 2^18) * 10^6 = 21.5759uV，要求噪音、干扰、漂移要小于21.5759微伏，只要舍得付出点代价，是有可能实现的。

20位分辨电压 = (5.656V / 2^20) * 10^6 = 5.3939uV，要求噪音、干扰、漂移要小于5.3939微伏，只要不惜代价，是有可能实现的。

当量化精度为16bit时，动态范围为96.32分贝，人耳的无痛苦极限声压是90分贝，已到极限。由于数码的阶梯效应，造成低位1/2不确定性，且无法克服，每一位可影响6分贝不确定性，16位采样刚好达到人耳的无痛苦极限声压90分贝，仅是理论计算值。为了实现真正的90分贝或大于90分贝，则要提高量化精度，17位从来没有过，那就18位了。再高已无意义，16位的细度已无法分辨。为什么选择90分贝，因为是人耳的无痛苦极限。