单通道和多通道影象的区别？

Posted 2023-03-25

参考技术A 　　在做机器视觉时，常常要将一个多通道影象分离成几个单通道影象或者将几个单通道影象合成一个多通道影象，以方便影象处理，加深单通道影象和多通道影象这两个概念的理解。
　　单通道和多通道影象相关概念
　　影象通道在RGB色彩模式下就是指在下就是指那单独的红色R、绿色G、蓝色B部分。也就是说，一幅完整的影象，是由红色绿色蓝色三个通道组成的。他们共同作用产生了完整的影象。同样在HSV色系中指的是色调H，饱和度S，亮度V三个通道。除了这两个三通道影象模式，以下列举了还列举一些影象模式
　　影象模式
　　1、点阵图模式

　　点阵图模式是1位深度的影象。它只是黑和白两种颜色。它可以由扫描或置入黑色的向量线条影象生成，也能由灰度模式或双色调模式转换而成。其他影象模式不能直接转换为点阵图模式。

　　2、灰度模式

　　灰度模式是8位深度的影象模式。也就是28，28=256，在全黑和全白之间插有254个灰度等级的颜色来描绘灰度模式的影象。

　　所有模式的影象都能换成灰度模式，甚至点阵图也可转换为灰度模式。Photoshop几乎所有的功能都支援灰度模式。

　　3、双色调模式

　　双色调模式不是单个的影象模式，而是一个分类。它仅仅是单色调、双色调、三色调和四色调的一个统称。双色调模式只有一个通道。双色调模式和点阵图模式一样，也只有灰度模式才能转换。

　　4、RGB模式

　　RGB模式是数码影象中最重要的一个模式，Photoshop的全部功能都支援它，因为Photoshop就是以它为基础来开发的。显示屏上显示的颜色是RGB模式，电视萤幕也是RGB模式，所不同的它不是用数码而是用电平来描述的。扫描器和数码相机都是捕捉RGB影象资讯的。

　　RGB模式是相加的模式，当R、G、B的值都达到最大值时，三色合成便成白色。

　　RGB模式是24位颜色深度。它共有三个通道，每个通道都有8位深度。三个通道合成一起可生成1677万种颜色，我们也称之谓“真彩色”。

　　5、CMYK模式

　　CMYK模式是用来列印或印刷的模式，它是相减的模式，当C、M、Y三值达到最大值时，在理论上应为黑色，但实际上因颜料的关系，呈显的不是黑色，而是深褐色。为弥补这个问题，所以加进了黑色K。

　　由于加了黑色，CMYK共有四个通道，正因为如此，对于同一个影象档案来说，CMYK模式比RGB模式的资讯量要大四分之一。

　　但RGB模式的色域范围比CMYK模式大。因为印刷颜料在印刷过程中不能重现RGB色彩。

　　CMY和RGB为互补色。

　　C-青色：由G-绿色和B-蓝色合成，其中没有R-红色成份;

　　M-洋红：由R-红色和B-蓝色合成，其中没有G-绿色成份;

　　Y-黄色：由R-绿色和G-红色合成，其中没有B-蓝色成份;

　　CMYK模式不能转换为索引模式。

　　Photoshop的大部分功能不支援CMYK模式

　　6、Lab模式

　　Lab模式是24位颜色深度的影象模式，有三个通道。L通道是亮度通道Lightness，a和b两个为色彩通道。它的特点在于：

　　1他的色域范围最广，它和RGB与CMYK模式的关系如下：

　　就色域范围而言Lab>RGB>CMYK

　　2此模式下的影象是独立于装置外的，它的颜色不会因不同的印刷装置，显示器和操作平台而改变。由于它有以上的有点，当Photoshop把RGB模式和CMYK模式互相转换时，它成为中间模式，颜色资讯就不会因以上两模式的色域范围不同而丢失。

　　a分量是由绿色向红色过度。

　　B分量是由蓝色向黄色过渡。

　　Lab模式不能转换为索引模式。

　　Photoshop的大部分功能不支援Lab模式。

　　7、索引颜色模式

　　索引颜色模式是8位颜色深度模式，它最多只能拥有256种颜色。

　　1每一副影象都各自拥有一张颜色表，而随影象不同，颜色表也不同。这一点是至关重要的。

　　2它的资讯量小，又可制动画，所以它的影象和动画被广泛地用于网页制作上。

　　3它可制成透明影象，在网页使用。

　　在转换时，只有灰度和RGB两种模式，不能转换成索引颜色模式。

　　转换时只有两个选择是实用的：

　　随样性 当影象颜色数大于256时，使用该选项，Photoshop会定做颜色表。实际当影象颜色小于256时，使用该选项，就用实际的颜色制作颜色表。

　　Photoshop完全不支援索引颜色模式。

　　8、多通道模式

　　多通道模式是把含有通道的影象分割成单个的通道。

　　CMYK模式转为多通道模式时，生成的通道为青色、洋红、黄色和黑色四个通道。

　　Lab模式转为多通道模式时，生成三个Alpha通道。

　　9、8位/通道和16位/通道

　　在灰度、RGB和CMYK模式下可以用每个通道16位深度来取代8位深度。那么，每个通道的颜色数从256色剧增到65536色，可生成更好的颜色细节。
　　目前，由于装置的不支援，16位/通道的影象不能被列印或印刷。 猜你喜欢

卷积神经网络多输入通道和多输出通道（channels）

多输入通道和多输出通道（channels）

• 5.3 多输入通道和多输出通道
• • 5.3.1 多输入通道
  • 5.3.2 多输出通道
  • 5.3.3 $1\times 1$卷积层
  • 小结

5.3 多输入通道和多输出通道

前面两节里我们用到的输入和输出都是二维数组，但真实数据的维度经常更高。例如，彩色图像在高和宽2个维度外还有RGB（红、绿、蓝）3个颜色通道。假设彩色图像的高和宽分别是$h$和$w$（像素），那么它可以表示为一个$3\times h\times w$的多维数组。我们将大小为3的这一维称为通道（channel）维。本节我们将介绍含多个输入通道或多个输出通道的卷积核。

5.3.1 多输入通道

当输入数据含多个通道时，我们需要构造一个输入通道数与输入数据的通道数相同的卷积核，从而能够与含多通道的输入数据做互相关运算。

假设输入数据的通道数为$c_i$，那么卷积核的输入通道数同样为$c_i$。设卷积核窗口形状为$k_h\times k_w$。当$c_i=1$时，我们知道卷积核只包含一个形状为$k_h\times k_w$的二维数组。当$c_i>1$时，我们将会为每个输入通道各分配一个形状为$k_h\times k_w$的核数组。把这$c_i$个数组在输入通道维上连结，即得到一个形状为$c_i\times k_h\times k_w$的卷积核。

由于输入和卷积核各有$c_i$个通道，我们可以在各个通道上对输入的二维数组和卷积核的二维核数组做互相关运算，再将这$c_i$个互相关运算的二维输出按通道相加，得到一个二维数组。这就是含多个通道的输入数据与多输入通道的卷积核做二维互相关运算的输出。

图5.4展示了含2个输入通道的二维互相关计算的例子。在每个通道上，二维输入数组与二维核数组做互相关运算，再按通道相加即得到输出。图5.4中阴影部分为第一个输出元素及其计算所使用的输入和核数组元素：$(1\times 1+2\times 2+4\times 3+5\times 4)+(0\times 0+1\times 1+3\times 2+4\times 3)=56$。

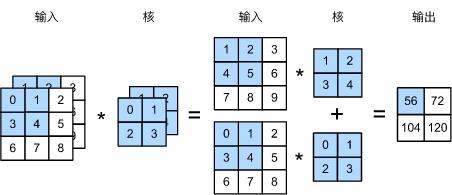
图5.4 含2个输入通道的互相关计算

接下来我们实现含多个输入通道的互相关运算。我们只需要对每个通道做互相关运算，然后通过add_n函数来进行累加。

import torch
from torch import nn
import sys
sys.path.append("..") 
import d2lzh_pytorch as d2l

def corr2d_multi_in(X, K):
    # 沿着X和K的第0维（通道维）分别计算再相加
    res = d2l.corr2d(X[0, :, :], K[0, :, :])
    for i in range(1, X.shape[0]):
        res += d2l.corr2d(X[i, :, :], K[i, :, :])
    return res

我们可以构造图5.4中的输入数组X、核数组K来验证互相关运算的输出。

X = torch.tensor([[[0, 1, 2], [3, 4, 5], [6, 7, 8]],
              [[1, 2, 3], [4, 5, 6], [7, 8, 9]]])
K = torch.tensor([[[0, 1], [2, 3]], [[1, 2], [3, 4]]])

corr2d_multi_in(X, K)

输出：

tensor([[ 56.,  72.],
        [104., 120.]])

5.3.2 多输出通道

当输入通道有多个时，因为我们对各个通道的结果做了累加，所以不论输入通道数是多少，输出通道数总是为1。

设卷积核输入通道数和输出通道数分别为$c_i$和$c_o$，高和宽分别为$k_h$和$k_w$。如果希望得到含多个通道的输出，我们可以为每个输出通道分别创建形状为$c_i\times k_h\times k_w$的核数组。将它们在输出通道维上连结，卷积核的形状即$c_o\times c_i\times k_h\times k_w$。在做互相关运算时，每个输出通道上的结果由卷积核在该输出通道上的核数组与整个输入数组计算而来。

下面我们实现一个互相关运算函数来计算多个通道的输出。

def corr2d_multi_in_out(X, K):
    # 对K的第0维遍历，每次同输入X做互相关计算。所有结果使用stack函数合并在一起
    return torch.stack([corr2d_multi_in(X, k) for k in K])

我们将核数组K同K+1（K中每个元素加一）和K+2连结在一起来构造一个输出通道数为3的卷积核。

K = torch.stack([K, K + 1, K + 2])
K.shape # torch.Size([3, 2, 2, 2])

print(torch.stack([torch.randint(1, 8, [2, 2]), torch.randint(1, 8, [2, 2])]).shape)

tensor([[[1, 7],
         [7, 6]],

        [[5, 5],
         [2, 1]]])
torch.Size([2, 2, 2])

下面我们对输入数组X与核数组K做互相关运算。此时的输出含有3个通道。其中第一个通道的结果与之前输入数组X与多输入通道、单输出通道核的计算结果一致。

corr2d_multi_in_out(X, K)

输出：

tensor([[[ 56.,  72.],
         [104., 120.]],

        [[ 76., 100.],
         [148., 172.]],

        [[ 96., 128.],
         [192., 224.]]])

5.3.3 $1\times 1$卷积层

最后我们讨论卷积窗口形状为$1\times 1$（$k_h=k_w=1$）的多通道卷积层。我们通常称之为$1\times 1$卷积层，并将其中的卷积运算称为$1\times 1$卷积。因为使用了最小窗口，$1\times 1$卷积失去了卷积层可以识别高和宽维度上相邻元素构成的模式的功能。

实际上，$1\times 1$卷积的主要计算发生在通道维上。图5.5展示了使用输入通道数为3、输出通道数为2的$1\times 1$卷积核的互相关计算。值得注意的是，输入和输出具有相同的高和宽。输出中的每个元素来自输入中在高和宽上相同位置的元素在不同通道之间的按权重累加。假设我们将通道维当作特征维，将高和宽维度上的元素当成数据样本，那么$1\times 1$卷积层的作用与全连接层等价。

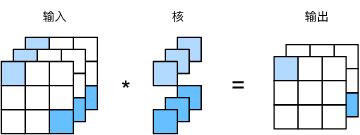
图5.5 1x1卷积核的互相关计算。输入和输出具有相同的高和宽

下面我们使用全连接层中的矩阵乘法来实现$1\times 1$卷积。这里需要在矩阵乘法运算前后对数据形状做一些调整。

def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.view(c_i, h * 
以上是关于单通道和多通道影象的区别？的主要内容，如果未能解决你的问题，请参考以下文章
 
 求助，关于心电图机的单通道和多通道
 机器学习-卷积神经网络CNN中的单通道和多通道图片差异
 卷积神经网络多输入通道和多输出通道（channels）
 NAudio WaveStream 和多通道
 文件列表遍历和多通道图片裁剪
 深度学习入门基础CNN系列——感受野和多输入通道多输出通道以及批量操作基本概念