分享一个很不错的车辆垂向动力学matlab工具箱
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了分享一个很不错的车辆垂向动力学matlab工具箱相关的知识,希望对你有一定的参考价值。
✅作者简介:热爱科研的算法开发者,Python、Matlab项目可交流、沟通、学习。
matlab二分之一车辆模型垂向动力学
1、内容简介
235
2、内容说明
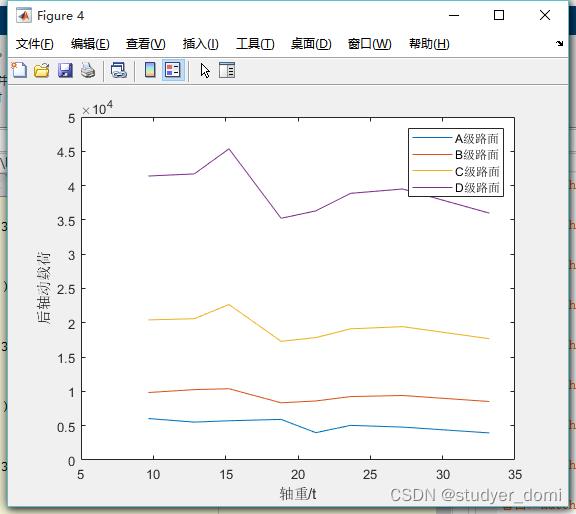
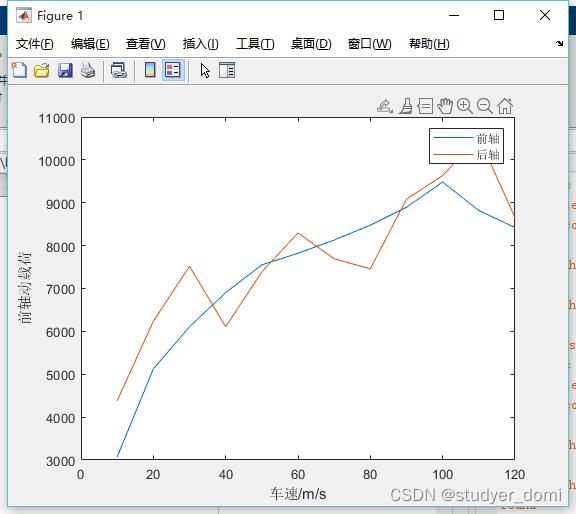
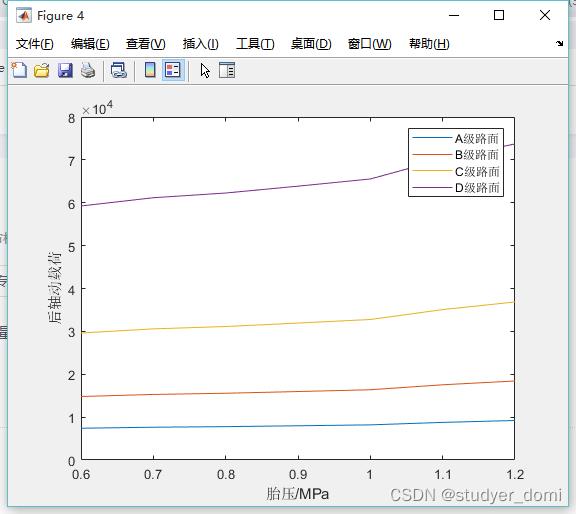
根据所建立的车辆模型,在不同车速、轴重、载荷、胎压,不同等级路面不平度下车辆对地面的动载荷和动载系数。车速、路面等级系数、车辆轴重、胎压、车辆重量等等最好可以是变化的量。
路面功率谱密度表达式:
(2—2)
式中:—参考空间频率,=0.1m-1;
—参考空间频率下的路面功率谱密度值,称为路面不平度系数;
w—频率指数,一般取w=2;
车辆以一定的速度v在空间频率Ω的路面上行驶时,需要通过转换将速度影响因子出现在PSD中,并将空间频率功率谱密度转换为时间功率谱密度。当车辆以恒速v经过空间频率Ω的路面时,时间频率f(Hz)为:
(2—15)
时间频率f和空间频率Ω的关系为:
(2—16)
时间频率功率谱密度和空间频率功率谱密度的关系为:
(2—17)
则时间频率功率谱密度为:
(2—18)
时间频率的不平度垂直速度的功率谱密度关系为:
(2—19)
时间频率的不平度加速度的功率谱密度关系为:
(2—20)
随机正弦三角级数法采用的表达式为式(2-8):
(2—8)
式中:—时间频率,与空间频率的关系为,;
—[0,2π]上均匀分布的随机数
时间频率时,在已知车速v的行驶下,可以经过计算来求得时间频率下的功率谱密度。由平稳随机过程平均功率的频谱的展开性质,得到路面不平度的方差为:
(2—21)
将区间划分成m个小区间,第i个小区间处的中心频率处的功率谱密度来代替第i个小区间整体上的功率谱密度值,得到第i个小区间上的方差为:
(i=1,2,,m) (2—22)
可以看作每个小区间内包含的功率。
路面不平度的方差的表达式(2—21)经过离散化后可近似表示为:
(i=1,2,,m) (2—23)
划分的每个小区间的频率为(i=1,2,,m),且其标准差为的正弦波函数表达式为:
(2—24)
将各个小区间的正弦波函数叠加在一起,即可得到时域路面随机激励:
(2—25)
式中:—[0,2]范围内的均匀分布随机数;
t—车辆行驶时间
同样,时域路面随机激励对时间求导,可以得到随机路面激励竖向速度值为:
(2—26)
再对式(2—26)进行时间t求导,即得到随机路面激励竖向加速度值:
(2—27)
当时间频率区间划分的m个小区间取的足够细密,m取的足够大时,式(2—25)计算仿真生成的时域随机路面谱的频率特征和给定路面谱一致。因此,生成的可以作为车辆在恒速v及给定的路面条件下的路面时域随机输入激励,经过傅里叶变换及其逆变换就可以换算得到路面频域随机输入激励。
地面作用于轮胎的时间频率一般介于0.5Hz30Hz,因此车辆振动系统的固有频率取f1= 0Hz,f2= 50Hz.城市市区内车辆速度一般为10km/h50km/h,省道道路和国道道路车速一般为40km/h80km/h,高速公路车速规定范围为60km/h120km/h。随着我国经济和科技的发展,高等级路面的建设越来越多,高等级路面在我国范围越来越广,逐步以高等级路面取代低等级路面。在本文进行研究时采用我国的路面功率谱标准,选取A、B、C、D三个等级的路面进行研究,路面不平度系数分别为:4、16、64、256×10-6m-2/m-1, 空间参考频率Ω0 =0.1m-1,频率指数w=2.
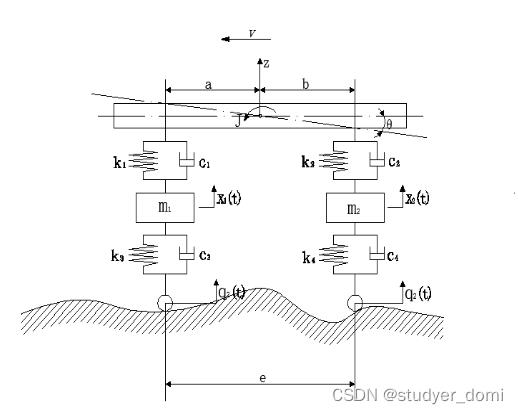
二分之一车辆模型
它将车辆前后轴统一在一个模型中,左、右轴之间的相互影响耦合作用视为很小。二分之一车辆模型假设,车辆模型简化为如图3-2所示。本模型中的四个自由度分别为:车身的垂直振动z,俯仰角度θ,前后车轮的垂向跳动x1和x2。m3— 悬架部分质量(又称为簧上质量),包括汽车的车厢和载重部分等等;
m1— 前轴簧下质量(又为前轴非悬挂部分质量),包括轮圈、轮胎、轮轴等;
m2— 后轴簧下质量(又为后轴非悬挂部分质量),包括轮圈、轮胎、轮轴等;
J—车身的转动惯量,单位为kg/m2; θ—车身俯仰摆角;
a, b— 汽车的前、后轴到质心的距离; v—汽车前进行驶速度和方向;
k1—前悬架系统的刚度系数; k2—后悬架系统的刚度系数;
k3—前轮胎的刚度系数; k4—后轮胎的刚度系数;
c1—前悬架系统的阻尼系数; c2—后悬架系统的阻尼系数;
c3—前轮胎的阻尼系数; c4—后轮胎的阻尼系数;
x1(t)—前轴簧下质量垂向位移; x2(t)—后轴簧下质量垂向位移;
z(t)—汽车模型车身垂向位移; e—前后轴距;
q1(t)—前轮路面不平度随机激励; q2(t)—后轮路面不平度随机激励;
本文中二分之一车辆模型的振动的微分方程为:
M+C+KX=f(t) (3—4)
展开式为:
(3—5)
(3—6)
(3—7) (3—8)
其中:
质量矩阵 M=;
阻尼矩阵 C=;
刚度矩阵 K=;
位移矩阵 X=;
激励矩阵 ;
进而可以求得出轮胎对路面的动荷载:
前后轮的动载系数为:
由于q1和q2为前后桥承受的路面不平度激励,这两个信号是相同的,均为第二章所仿真得出的路面不平度信号,但是它们之间只差了一个时间差,可以根据前后桥的距离及车辆的速度求出,,则.
前轴簧下质量m1=297kg
后轴簧下质量m2=524kg
簧上质量m3=6461kg
车身转动惯量J=46249N.m2
a=3.79m,b=2.31m,L=6.1m
前轮胎刚度系数k3=788100N/m
后轮胎刚度系数k4=875667N/m
前悬架刚度系数k1=198251N/m
后悬架刚度系数k2=1138367N/m
前轮胎阻尼系数c3—=2000Ns/m
后轮胎阻尼系数c4=2000Ns/m
前悬架阻尼系数c1=15000Ns/m
后悬架阻尼系数c2=15000Ns/m答1疑2咨3询4企q鹅q号:1762016542
3、仿真分析
4、参考论文
略
以上是关于分享一个很不错的车辆垂向动力学matlab工具箱的主要内容,如果未能解决你的问题,请参考以下文章