品味数学之美－RSA原理浅析

Posted 2023-03-17

参考技术A

在探究RSA算法的原理之前，我们先来学习一点有趣的数论知识（数学分支之一，主要研究整数的性质）。你会发现一些简单的数学知识竟然背后有如此神奇的魔力。

说起质数，想必大家不陌生了，一个大于1的整数除了其本身和1之外，不存在因数则被称为质数或者是素数。比如2、3、5、7等。在小学课堂里，我们可能只是记住了这个概念，但是这里我谈下自己的一些思考帮助大家理解，质数就好比是构成数字的基本元素，想想看，氢分子仅由两个氢原子（组成一个氢分子）构成，那么一个非质数的6=3*2 即表示为6是由两个“3”元素或3个“2”元素构成。其中“3”或者“2”是不可以继续拆分的元素（3，2都是质数）。所以对一个非质数进行因式分解过程就好比对一个物体进行深入解剖，拆分至不可拆分的元素为止。这样看来，数学家们提出这些数学概念，其实也是一种对数字世界的认识和思考的概括，和我们日常生活理解周边事物方式也是相似的。

知道了质数，我们再看看互质关系，那么什么是互质呢？就是说两个数没有相同的因数称为互质关系。我们对6进行因数分解，拆分到质数的乘积即6＝3* 2而 35=5*7,这两者没有相同的因数则称6与35互质，就好像氢气分子只是由氢原子构成，而氧气分子只是由氧原子构成，这二者这间没有相同的原子就是一种互质的体现。
所以互质只是一个数和数之间有没有相同的因数关系的体现(公约数也称公因数)，和两者是不是质数是没有关系的。当然质数之间必然是互质关系，因为它们都是构成数字的不同元素。数学上来表示a,b互质一般用gcd(a,b)=1来表示。即a和b的最大公约数是1.

质数和互质的关系是不是很容易理解？但是大数学家欧拉先生可绝不仅仅停步于此，数学家嘛总爱问一下抽象概括性的问题，希望找寻规律比如

如果能找到规律，无论数字如何千变万化10位数还是100000位数，我们都能根据准则轻易计算数互质关系的数量。你发现了没有，数字也是一片世界，真是一花一世界一叶一如来啊！好了回归正传，对于这个问题欧拉先生给出了他的答案。他是这样作答的：
首先呢上述问题可以简化为一个函数来描述即： \\Phi(n)
这也是数学家老毛病在他们看来任何问题就是对函数的求解。既然这个函数由欧拉提出来的，那么我们就称他为 欧拉函数 .还好这个函数简单只有一个变量，即给定的正整数n。接下来就要分析这个n

n＝1的时候这个问题极其简单：
\\Phi(n)＝1
因为1与任何数包含他自身都构成互质关系。1本身也是质数且不作为其他数的因数，因为任何数乘以1都是其本身

大家想想看n是质数，其自身就不存在因数了，而那些与他非互质关系(存在公约数)的数进行因式分解后一定都会有一个因数与n相等。比如n＝3为一个质数，那么6＝3*2与3是非互质关系，因为存在公约数3。所以我们发现与n非互质关系的数都是n的倍数即(kn)，因为kn>=n所以与n互质的数都小于n即
\\Phi(n)＝n-1

还记得我们前面提到的质数吗，他可是构成数字的元素呀，所以如果n不是质数，那么他一定可以被因式分解拆分成多个质数的乘积。比如24=6*4=3*8=2*2*2*3 比如6=2*3，这些质数因数相互乘积也可以形成如下情况：

我们把相同质数因数进行相乘，很容易将一个非质数分解为两个互质关系的数的乘积，比如24=6*4=2*2*2*3＝3*8
从简单的情况来考虑，即n被拆分为两个互质关系的数的乘积：
即

n=p*q
p与q互质，那么根据剩余定理:

\\Phi \\left( pq\\right) =\\Phi(p)*\\Phi(q)

至于如何证明呢？说实话我也不清楚。在我理解看来，与24互质的数都有这样一个特点：他进行因式分解后其因数不包含有3与2（因为8=2*2*2）。所以与3互质的数定义为集合A，且个数为
\\Phi \\left( 3\\right)
与8互质的数定义为集合B，且个数为
\\Phi \\left( 8\\right)
这AB两组的数字可以在组与组间两两进行组合乘积，构成与24互质的数。所以两组数字个数相乘就可以知道乘积的组合个数，也就知道与24互质的个数了。这样的证明并不严谨但姑且可以先记住。
另外还需要记住欧拉函数是一个 积性函数 ,也就是n如果为多个互质的数构成即(n=a*b*c*d.... )，那么
\\Phi \\left( n\\right)=\\Phi \\left( a\\right) *\\Phi \\left( b\\right)....

也就是n为某一个质数的倍数，比如27=3*3*3=3^3 27就是3的倍数。那么小于27且存在非互质关系的数一定都是3的倍数也就是：1*3、2*3,3*3...9*3 共计9个， 所以3^3 - 9 ＝3^3 - 3^2 .所以归纳一下也就是说如果p是质数，求与p^n 互质的数的个数，只要将如下的数
(1*p)、(2*p)、(3*p)、....(p^n-1 *p) 进行剔除，剩余的都将与p^n （切记p是质数）互质所以我们得出：

\\Phi \\left( p^k\\right)=p^k-p^k-1＝p^k(1-\\dfrac 1p )

当k＝1的时候即
\\Phi \\left( p\\right)=p-1
又回到了之前n为质数的情况下的表达式。这里我们也看到数学追求简洁和普适性的思想，再繁杂的规律都可以变成一个简洁抽象的表达式。

比如24=6*4=3*8=2*2*2*3，因为质数之间就是互质关系而且质数的多次方也是互质关系所以
我们把24演变一下：24=2^3 * 3即把相同的质数进行合并为质数的多次方。这样2^3 与3是互质关系( 质数的多次方之间也都是互质关系 )，于是当我们求与24互质的数的个数时候，就可以套用之前公式即：

\\Phi \\left(24\\right)=\\Phi \\left( 2^3*3\\right)=\\Phi \\left(2^3\\right)*\\Phi \\left(3\\right)=(2^3-2^3-1)(3-1) =8

再进一步归纳因为p1、 p2...pm等都是质数且
n = p_1^k_1p_2^k_2p_3^k_3...p_m^k_m

则由于欧拉函数是积性函数，那么：
\\Phi \\left(n\\right)=\\Phi \\left( p_1^k_1p_2^k_2p_3^k_3...p_m^k_m\\right) =\\Phi \\left( p_1^k_1\\right)* \\Phi \\left( p_2^k_2\\right)*...\\Phi \\left( p_m^k_m\\right)
由上一小节n为质数的多次方的结论
\\Phi \\left( p^k\\right)=p^k-p^k-1＝p^k(1-\\dfrac 1p )
可以得出：
\\Phi \\left( p_1^k_1\\right)* \\Phi \\left( p_2^k_2\\right)*...\\Phi \\left( p_m^k_m\\right)=p_1^k_1p_2^k_2...p_m^k_m*(1-\\dfrac 1p_1 )*(1-\\dfrac 1p_2)...(1-\\dfrac 1p_m )

则
\\Phi \\left(n\\right)=n*(1-\\dfrac 1p_1 )*(1-\\dfrac 1p_2)...(1-\\dfrac 1p_m)
此时我们仍然计算24互质个数则
\\Phi \\left(24\\right)=\\Phi \\left( 2^3*3\\right)=\\Phi \\left(2^3\\right)*\\Phi \\left(3\\right)=24*(1-\\dfrac 12)(1-\\dfrac 13)＝8

上面说的那么多其实归结起来就是这样一个道理：当我们去求小于某个数范围内与其互质的数的个数时候，无非就是把n分为质数还是非质数。

知道了欧拉函数，接下来我们再理解一个同余概念，简单来说也就是25除以3的余数为1，而1除以2的余数为1，则我们称25与1对于模3同余数，用人话来说就是25和1 除以2得到的余数都一样。求余数的过程在数学里的黑话叫取模。所以才有上面那么拗口的说法。但是不要紧，数学喜欢简单不啰嗦，于是搞出了如下的表达式来表达上述说法：
25\\equiv 1\\left( mod\\ 3\\right)
也就是说
25 \\% 3 = 1\\%3=1
注意到了吗？上述表达式也可以这样表述，即25除以3得到的余数为1.围绕着同余这个概念，欧拉大师结合他的欧拉函数活脱脱就搞出了个欧拉定理，我们来看看他有什么发现？

另外根据取模运算的规则：
a^b\\%p = ((a \\% p)^b) \\% p
我们还可以得出
（a^\\Phi \\left(n\\right))^k\\equiv 1\\left( mod\\ n\\right)
因为
(a^\\Phi \\left(n\\right))^k \\% n=（a^\\Phi \\left(n\\right)\\%n)^k\\%n=1^k\\%n =1
我们举个例子：比如
\\Phi \\left(10\\right)＝\\Phi \\left(2*5\\right)=\\Phi \\left(2\\right)*\\Phi \\left(5\\right)=(2-1)*(5-1)=4

所以根据欧拉定理：因为9与10互质所以
9^\\Phi \\left(10\\right)=9^4\\equiv 1\\left( mod\\ 10\\right)
于是(9^4 )^k 除以10都余1。

如果a与n互质，则必然能够找到一个数使得
ab\\equiv 1\\left( mod\\ n\\right)
则b称为a的模反元素，我们可以通过欧拉定理来给予证明
a^\\Phi \\left(n\\right)=1\\left( mod\\ n\\right)
a^\\Phi \\left(n\\right)= a*a^\\Phi \\left(n\\right)-1\\equiv 1\\left( mod\\ n\\right)

模反元素的概念对后续在已知道公钥情况下，计算合适的私钥是有很重要的意义的。
掌握了这些数学知识，你可能觉得这些东西似乎很孤立，看不到任何作用和价值，不过接下来我们来看看RSA是怎么运作的，你就会发现这些看似毫无作用的东西是如何产生价值的。

从加解密的表达式可以看出在，数学原理上公钥和私钥其实并没有什么差异。你可以用公钥加密、私钥解密，也可以用私钥加密，公钥进行解密。但是对于密码学来说，对公钥和私钥会有不同的要求。
另外需要注意的是这里 明文数值不能大于等于N ，否则解密的结果并不会等于明文。

因为加密的公式为：
x^e mod n = y
而解密公式为
y^d mod n = x
从上面表达式可以看出在数学原理上公钥和私钥其实并没有什么差异。你可以用公钥加密、私钥解密，也可以用私钥加密，公钥进行解密。
所以根据：
y=x^e - kn
且因为Y^D mod N = x 所以
y^D \\equiv x (mod\\ n)
所以确定能否加解密的过程本质就是证明：
（x^e - kn)^d \\equiv x (mod\\ n) （1.1）
而根据二项式定理
[图片上传失败...(image-ca75c7-1530364603810)]

（x^e - kn)^d 展开后演变为
x^ed-m_1x^e(d-1)kn+m_2x^e(d-2)(kn)^2...m_n(kn)^d
你会发现二项式展开后，唯有x^ed 没有包含n，因此结合模运算加法运算规则(a + b) % p = (a % p + b % p) % p ，要想证明1.1的表达式，则必然证明：
x^ed \\equiv x (mod\\ n)
由于
ed \\equiv 1 (mod\\ \\Phi \\left(n\\right))
所以
ed=h\\Phi \\left(n\\right))+1
则从证明
x^ed \\equiv x (mod\\ n) 演变为证明
x^h\\Phi \\left(n\\right)*x\\equiv x (mod\\ n)
如果x与n 互质则根据欧拉定理
x^\\Phi \\left(n\\right)\\equiv 1 (mod\\ n)
基于在欧拉定理中提及的，根据取模运算规则可以得出
x^h\\Phi \\left(n\\right)\\equiv 1 (mod\\ n)
仍然是基于取模运算乘法规则，我们又可以得出
x^h\\Phi \\left(n\\right)x\\equiv x (mod\\ n)
这样原式得到证明。
那么如果x与n不互质的情况下，因为n=p*q且p和q都是质数，所以n的因数只有p和q了，因为x与n不互质，那么我们可以认为：
x=k_1p 0 < u< q
或者
x=k_2q 0 < k

请注意k值的取值范围，这里要牢记一点明文值必须大于0且小于n值。
这里我们先姑且定义
x=kq
0 < k< p

那么因为p与q都是质数，根据k<p 我们可以认为k与p是互质的，而p本身就是质数，所以根据费尔马小定理（n
为质数，a与n互质，如果有所遗忘可以回到前面查看相关说明。）
a^n-1\\equiv 1\\left( mod\\ n\\right)
那么
(kq)^p-1\\equiv 1\\left( mod\\ p\\right)
根据费尔马定理我们推得出来的表达式
a^\\Phi \\left(n\\right)\\equiv 1\\left( mod\\ n\\right)
得出
((kq)^p-1)^h*(q-1)\\equiv 1\\left( mod\\ p\\right)
也就是
(kq)^h*(q-1)(p-1)\\equiv 1\\left( mod\\ p\\right)
根据取模运算的运算定义：

得出

(kq)^h*(q-1)(p-1) = 1+u*p
这里的u为任意整数，这时候两边都乘以kq
(kq)^h*(q-1)(p-1)*kq = 1+u*k*q*p
因为n=pq x=kq那么
(x)^\\Phi \\left(n\\right)+1 = x+u*k*n
还是根据之前取模运算定义得出
(x)^h\\Phi \\left(n\\right)+1\\equiv x\\left( mod\\ n\\right)
即原式得到了证明。

之所以RSA是安全的，很大程度取决于n值是否足够大以至于在已知公钥e和模数n的情况下仍然难以找出d。根据之前的谈及的密钥对计算方式：
E*D \\equiv 1(mod\\ M)
要想算出D就必须计算出M 而M = (p-1)(q-1) ，n=p*q则要算出M就需要知道p和q，即从一个庞大的数中分离出两个也很大的质数。大数的素因数分解被认为是一个困难的问题，即使是现代的计算机也非常难于处理，所以许多加密系统的原理都是建基于此。
目前最安全的做法是选择使用rsa-2048，随着2009年12月12日，编号为RSA-768（768 bits, 232 digits）数也被成功分解。这一事件威胁了现通行的1024-bit密钥的安全性。这里的2048表示的是模数N
的二进制位为2048位。而一般公钥世面上普遍选择65535，这是安全性和计算速度之间的综合考虑下选择出来的一个比较妥当的数值。因为加解密函数都是在做大数的指数运算，所以在工程方面会尽量考虑公钥加解密的执行速度，毕竟公钥是被外部使用的。
此外还记得前面提到rsa加密的明文数值大小不能大于N，或者其位数不能超过N的位数的限制。一旦超过密文解密后和原文数据不相匹配，这时候就需要采用分段加密技术。而另一方面明文的值也不能为0或1，-1因为这样导致密文也是0，1或者-1。另外也有一个问题即如果用私钥解密一段非法数据，那么得到是解密失败还是一个毫无意义的解密内容呢？这时候需要采用 rsa padding技术。对这个概念理解可以参考 浅谈RSA Padding 这篇文章。

通过学习一些简单的数论知识即质数、欧拉函数、模反元素等概念后，我们也了解RSA算法大致过程，总的来说公私密钥对需要计算如下几个数据：

RSA的安全性不仅仅建立于大数质因数分解困难这一理论基础上，在工程上如何对上述这些数值的选取也是很大的学问。通过对rsa学习让我对工程和理论之间的关系理解上更进一步。理论确定了方向的可行性，而工程实践则要确保在有限资源下，理论结果是可以应用起来解决特定规模的问题。而在加密算法领域，一旦工程实践出现偏差，往往就容易产生安全漏洞，尽管算法理论证明是安全的。比如rsa中p q值的选择等。这里我罗列几个工程问题有兴趣的童鞋可以再进一步做探索：

多线程之美4一 线程池执行原理浅析

目录结构

引言
一、线程池工作流程图
二、线程池的运行原理
三、线程池的7个参数
四、常用4个阻塞队列
五、四个拒绝策略语义以及测试用例
六、Executors工具类
6.1. Executors提供的三种线程池
6.2 实际开发中应该怎样设定合适线程池？
七、线程池提交任务的2种
八、总结

---

引言

? 我们为什么要使用线程池，它可以给我们带来什么好处？要想合理使用线程池，我们需要对线程池的工作原理有深入的理解和认识，让我们一起来看看吧。

好处：

? 1、处理响应快，不用每次任务到达，都需要等待初始化创建线程再执行，到了就能拿来用。

? 2、资源复用，减少系统资源消耗，减低创建和销毁线程的销毁。

? 3、可方便对线程池中线程统一分配，调优，监控，提高系统稳定性。

一、线程池工作流程图

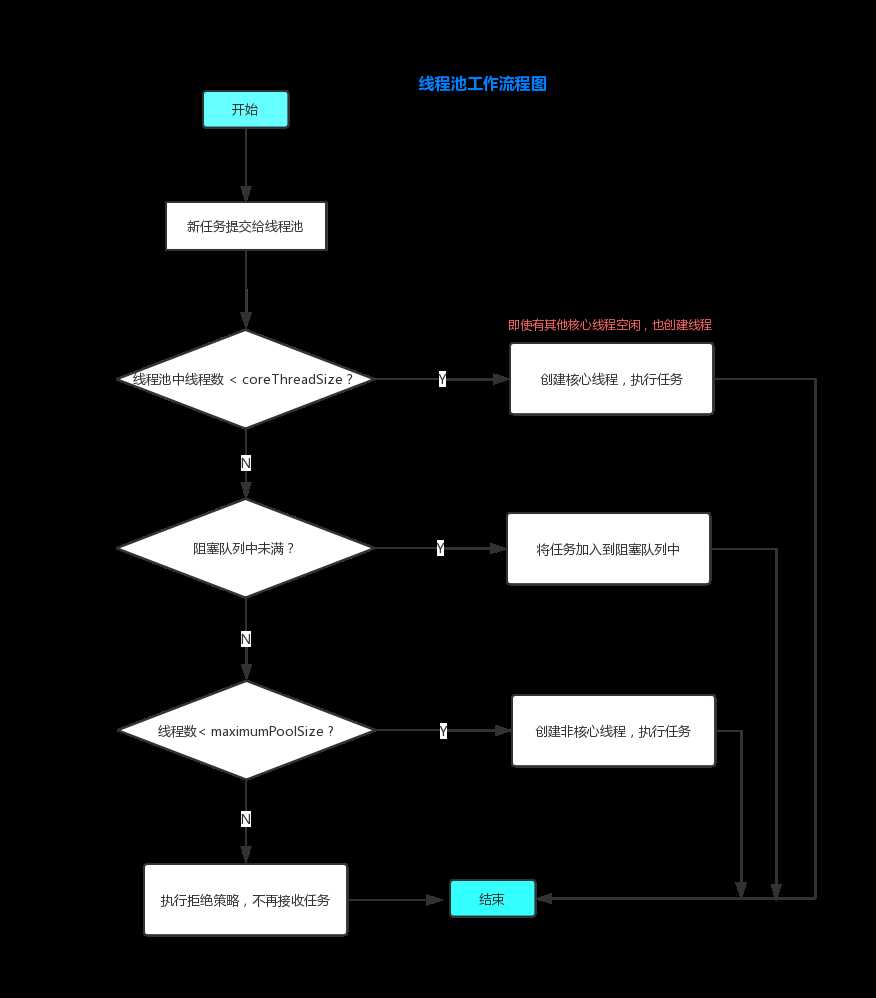
误区: 有没有人之前和我一样，以为当线程池中线程达到最大线程数后，才将任务加入阻塞队列？

二、线程池的运行原理

先讲个小故事，一个银行网点的服务过程：

如某银行网点,总共有窗口5个,提供固定座椅3个供客人休息, 在非工作日窗口并不是全都开放，而是安排轮值窗口，比如开放2个窗口给客户办理业务。当客户1,2 进网点办理业务,可直接去窗口办理,后又来了3位客户,这三位客户只能取号在座椅等待, 这时如果再来3位客户,这时座椅不够坐了，大堂经理为了尽快给客户办理，只好增派人手,开放其他3个窗口;
这时5个窗口全部开放为客户办理业务,座椅还有3位客户排号等待；这时正值客流高峰期,如果再来客户办理业务,网点接待不过来,为了不让客户等待太长时间，这时可以对再来客户劝说选择其他时间过来，或者去其他就近网点办理。当客户高峰过去,客户逐渐稀少，这时临时增派人手的窗口工作人员就可以关闭窗口,只保留轮值2个窗口继续提供服务。

类比银行的服务过程，线程池的执行原理与之相似：

线程池中一开始没有线程,在有新任务加入进来，才创建核心线程处理任务,(针对某些业务需求,可以线程池预热执行prestartAllCoreThreads()方法,可以在线程池初始化后就创建好所有的核心线程)。当多个任务进来,线程池中的线程来不及处理完手上任务,就创建新的线程去处理，当线程数达到核心线程数（ corePoolSize),就不再创建新的线程了，再有多的任务添加进来，加入阻塞队列等待；这里核心线程就如银行网点的轮值窗口，阻塞队列就如网点中的座椅, 但是网点中座椅是有限的，而线程池中的阻塞队列有可能接近无限,下文会详细讲述几种队列,这里假定线程池中队列也是有限的，在新加入的任务在阻塞队列中已经装不下的时候，这时就得加派人手,如果线程池中还没有达到最大线程数，创建新的线程来处理任务，如果线程池已经达到最大线程数，如网点办理窗口都开放了，等候区的椅子也坐满了客户，这时就得执行拒绝策略，不再接收新的任务；实际的拒绝策略方式更灵活，这里如此便于理解，下文再深入探讨。当线程处理完阻塞队列中任务，新加入的任务减少，或者没有任务添加，线程池中的非核心线程在空闲一定时间（keepAliveTime）后就被回收，可以节约资源。核心线程不会被回收，等待处理新加入的任务。

类比关系：

线程池 --> 银行网点
线程 --> 办理业务的窗口
任务 --> 客户
阻塞队列 --> 等候区的座椅
核心线程数 --> 轮值的窗口
最大线程数 --> 网点可以开放的所有窗口

三、线程池的7个参数

  public ThreadPoolExecutor(int corePoolSize,
                              int maximumPoolSize,
                              long keepAliveTime,
                              TimeUnit unit,
                     BlockingQueue<Runnable> workQueue,
                            ThreadFactory threadFactory,
                      RejectedExecutionHandler handler)

• 1、corePoolSize, 核心线程数
• 2、maximumPoolSize, 线程池中可以创建的最大线程数
• 3、keepAliveTime, 这个参数仅对非核心线程有效,当非核心线程空闲（没有任务执行）超过keepAliveTime时间就会被回收。
• 4、unit, keepAliveTime的时间单位, 如秒,分等
• 5、workQueue，阻塞队列，用于存放提交的任务, 在没有空闲的核心线程时，新加入的任务放入阻塞队列中等待执行。
• 6、threadFactory，用于创建线程的工厂。
• 7、handler,用于拒绝新添加的任务，当线程池中阻塞队列已满, 且线程池中已经达到最大线程数，再有新的任务提交进来，执行的拒绝策略。

四、常用4个阻塞队列

1) ArrayBlockingQueue 底层数组
2) LinkedBlockingQueue 底层链表
3) SynchronousQueue 不存储元素的队列， 没有容量的阻塞队列，每个插入操作必须等待另一个线程的对应移除操作,较难理解，见下文示例分析。

4)PriorityBlockingQueue: 优先级排序队列，优先级高的任务先被执行，可能会导致优先级低的始终执行不到，导致饥饿现象。

注：在Executos工具类提供的三种线程池中， FixedThreadPool，SingleThreadExecutor都使用的LinkedBlockingQueue 链表结构的队列， CachedThreadPool使用的SynchronousQueue没有容量的队列。

五、四个拒绝策略语义以及测试用例

1、AbortPolicy: 直接抛出异常 （默认方式）
2、CallerRunsPolicy: 抛给调用者去执行任务，如谁创建了线程池提交任务进来，那就找谁去执行，如主线程
3、DiscardOldestPolicy: 丢弃在队列中时间最长的，即当前排在队列首位的（先进来的任务),开发中是有适用业务场景，如等待最久的任务已经不具有再执行的意义了，如时效性比较强的业务。或者业务可允许一些任务。
4、DiscardPolicy: 新加入的任务直接丢弃，也不抛异常，直接不处理。

示例如下：

• 1、AbortPolicy 策略

提交9个任务，超出线程池可最大容纳量8个

package ThreadPoolExcutor;

import java.util.concurrent.*;

/**
 * @author zdd
 * 2019/12/1 11:16 上午
 * Description: 测试线程池4中拒绝策略
 */
public class ExcutorTest1 {

    public static void main(String[] args) {

     //   System.out.println("cpu number:"+ Runtime.getRuntime().availableProcessors());

         //实际开发中 自己创建线程池
        //  核心线程数2，最大线程数5，阻塞队列容量3，即最大可容纳8个任务，再多就要执行拒绝策略。
        ExecutorService executorService = new ThreadPoolExecutor(
                2,
                5,
                1L,
                TimeUnit.SECONDS,
                new LinkedBlockingQueue<Runnable>(3),
                Executors.defaultThreadFactory(),
                new ThreadPoolExecutor.AbortPolicy());

        //提交9个任务，超出线程池可最大容纳量8个 
        for (int i = 0; i < 9; i++) { 
           final int index =i+1;
           //此时任务实际还未被提交，打印只是为了方便可见。
            System.out.println("任务"+index +"被提交");
            executorService.execute(()-> {
                try {
                    //休眠1s,模拟处理任务
                    TimeUnit.SECONDS.sleep(1); } catch (InterruptedException e) { e.printStackTrace();
                }
                System.out.println(Thread.currentThread().getName()+ " 执行任务" +index);
            }) ;
        }

        executorService.shutdown();
    }
}

执行结果：直接抛出异常

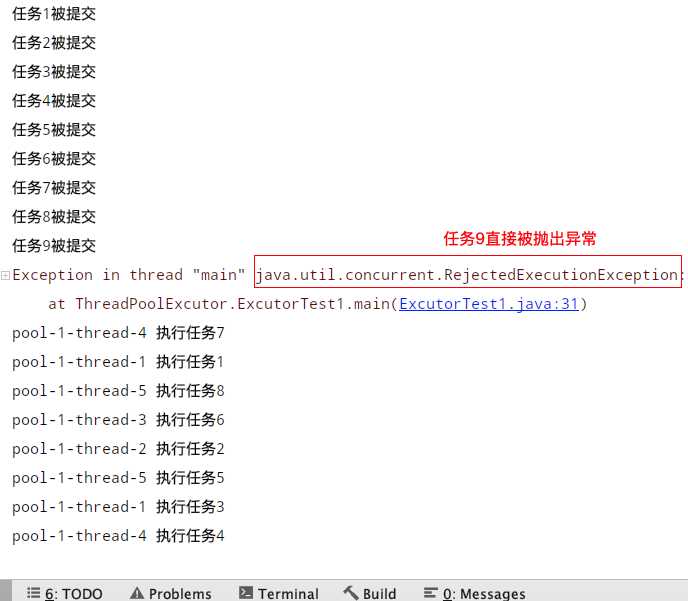
• 2、CallerRunsPolicy策略

new ThreadPoolExecutor.CallerRunsPolicy() //线程池采用该策略

执行结果：可见任务9被调用者主线程执行

• 3、DiscardOldestPolicy策略

   new ThreadPoolExecutor.DiscardOldestPolicy()) 

执行过程： 任务1，2提交直接创建核心线程执行，任务3，4，5依次被放入阻塞队列中，任务6，7，8再提交创建非核心线程执行，此时任务9提交进来，执行拒绝策略，将阻塞队列中排在首位的任务3丢弃，放入任务9。

执行结果： 可见任务3被丢弃了，未执行。

• 4、DiscardPolicy 策略

new ThreadPoolExecutor.DiscardPolicy() //修改此处策略

执行结果： 可见有9个任务被提交，实际就8个任务被执行，任务9直接被丢弃

六、Executors工具类

Executors, Executor,ExecutorService, ThreadPoolExecutor 之间的关系？

如下类图所示：

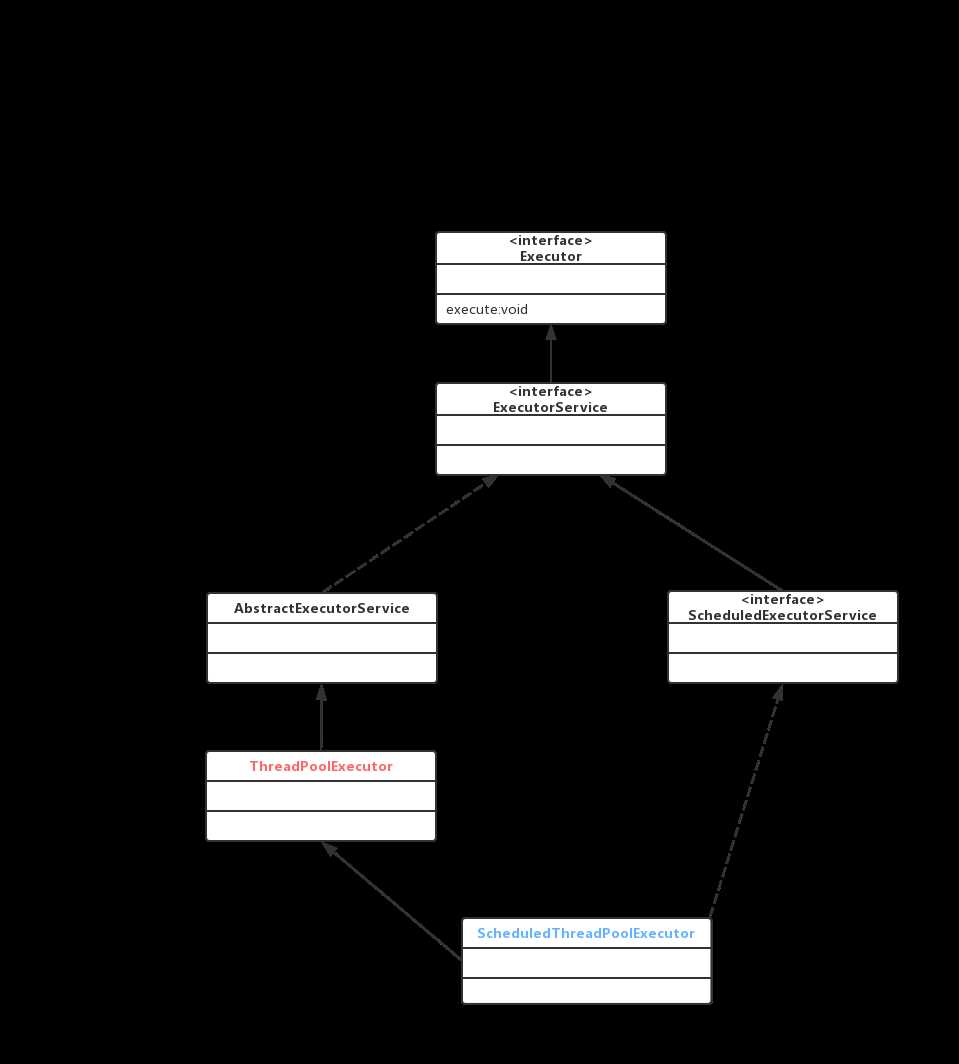
Executors是一个工具类,就如集合中Collections 一样，可以提供一些辅助的方法便于我们日常开发，如帮助创建线程池等。

在线程池中核心的类是上图颜色标识的ThreadPoolExecutor和 SchduledThreadPoolExecutor 两个类

• ThreadPoolExecutor：创建线程池核心类，可以根据业务自定义符合需求的线程池。

• SchduledThreadPoolExecutor：用于操作一些需要定时执行的任务，或者需要周期性执行的任务，如Timer类的功能，但是比Timer类更强大，因为Timer运行的多个TimeTask 中，只要其中之一没有被捕获处理异常，其他所有的都将被停止运行，SchduledThreadPoolExecutor没有这个问题。

6.1. Executors提供的三种线程池

Exectutos为我们提供了FixedThreadPool, SingleThreadExecutor, CachedThreadPool 三种线程池，

实际工作中如何使用线程池、用jdk工具类Excutors提供的三类，还是自己写，为什么？

• 1、固定数量线程的线程池 - FixedThreadPool

//1,固定数量线程池
public static ExecutorService newFixedThreadPool(int nThreads) {
  
        return new ThreadPoolExecutor(
          nThreads, 
          nThreads,
           0L, 
          TimeUnit.MILLISECONDS,
           new LinkedBlockingQueue<Runnable>());
    }

 //2,可见队列默认大小非常大
  public LinkedBlockingQueue() {
        this(Integer.MAX_VALUE);
    }
/** 
解析：
Integer.MAX_VALUE = 2^31 -1,大概21亿,近似无界队列
1）核心线程数== 最大线程数
2）阻塞队列近似无界
3)由于1，2，空闲线程的最大生存时间(keepAliveTime)也是无效的,不会创建其他非核心线程

存在问题：网上有推荐使用该种方式创建线程池，因为有一个无界的阻塞队列，在生产环境出现业务突刺（访问高峰，任务突然暴增等),不会出现任务丢失；可一旦出现该种情况，阻塞队列就算无界，服务器资源，如内存等也是有限的，也无法处理如此多的任务，有OOM(内存溢出)的风险，也不是推荐的方法。
**/

• 2、仅有一个线程处理任务- SingleThreadExecutor

public static ExecutorService newSingleThreadExecutor() {
        return new FinalizableDelegatedExecutorService
            (new ThreadPoolExecutor(1, 1,
                                    0L, TimeUnit.MILLISECONDS,
                                    new LinkedBlockingQueue<Runnable>()));
    }

/**
解析：

1）核心线程 =最大线程数=1，线程池中仅有1个线程
2）采用无界阻塞队列

1,2,可以实现所有的任务被唯一的线程有序地处理执行。
**/

• 无界线程数量 -- CachedThreadPool

//线程最大线程数近似无界
public static ExecutorService newCachedThreadPool() {
        return new ThreadPoolExecutor(0, Integer.MAX_VALUE,
                                      60L, TimeUnit.SECONDS,
                                      new SynchronousQueue<Runnable>());
    }  

/**
解析：
1)核心线程数 ==0
2）最大线程数无界
3）采用没有容量的阻塞队列
4）空闲线程可存活60s,超过60s无新任务进来就会被回收。
5）如果主线程提交任务的速度大于线程处理任务的速度时，会不断创建新的线程，因最大线程数时无界的，极端情况有可能耗尽cup和内存资源。
6）SynchronousQueue 队列既然没有容量，是怎样是机制实现添加任务和线程获取任务去执行的呢？

那要实现添加和获取任务的配对：即 offer()和 poll() 方法的配对

从添加角度看：主线程添加任务到线程池中（调用SynchronousQueue.offer(task)），当前没有空闲线程可用,则创建新线程处理,有空闲线程给它执行。

从获取角度看：线程池中线程处理完手上任务后，去阻塞队列获取新的任务（调用SynchronousQueue.poll()方法），没有任务空闲的线程在SynchronousQueue中等待最多60s,即空闲线程去队列中等待任务提交,在这期间主线程没有新任务提交，线程就会被回收，如有新任务提交则处理执行。免于被回收的厄运； 当线程池中较长时间没有新任务添加，整个线程池都空闲时，线程都会被回收，此时没有线程存在，可节约资源。
**/

在分析了Executors工具类提供的创建三种线程池, 虽然简单易用，但在实际开发中我们却不建议使用，因此我们需要根据公司业务来自己创建线程池。在阿里巴巴的Java开发手册中也强制不让使用Executors去创建线程池，都有OOM的风险。如：

6.2 实际开发中应该怎样设定合适线程池？

cpu 密集型任务：尽量创建少一些线程 , cpu个数+1

IO 密集型任务： 线程数可以多一些，cup个数*2

//可获取当前设备的cpu个数
Runtime.getRuntime().availableProcessors()

七、线程池提交任务的2种

• execute(): 提交任务无返回值
• submit() ：有返回值，可获取异步任务的执行结果。

void execute(Runnable command)  
//分割线 ---
Future<?> submit(Runnable task)
Future<T> submit(Callable<T> task)

示例: 使用线程池的submit提交异步任务，主线程调用 FutureTask的get() 方法，在异步任务未执行完毕前，主线程阻塞等待，异步任务执行结束，获取到返回结果。

适用场景 ：当一个线程需要开启另一个线程去执行异步任务，而需要异步任务的返回结果，存在数据依赖关系，在实际开发中，可将一次任务拆分为多个子任务，开启多个线程去并发执行，最后异步获取结果，能有效提高程序执行效率。

代码如下：

package ThreadPoolExcutor;

import java.util.concurrent.*;

/**
 * @author zdd
 * 2019/12/5 7:22 下午
 * Description:测试 Callable与FutureTask的简单实用，执行异步任务
 */
public class ThreadPoolSubmitTest {
    public static void main(String[] args) throws ExecutionException, InterruptedException {
       //1,创建线程池
       ExecutorService threadPool =  Executors.newFixedThreadPool(5);
        Callable callableTask = new Callable() {
            @Override
            public Object call() throws Exception {
                try {
                    //1,一个异步任务,模拟执行一个比较耗时的业务。休眠3s
                    TimeUnit.SECONDS.sleep(3);
                    System.out.println("休眠3s结束！ ");
                } catch (InterruptedException e) {
                    e.printStackTrace();
                }
                //2,返回执行结果
                return "ok!";
            }};

       FutureTask<String> futureTask = new FutureTask(callableTask);
       threadPool.submit(futureTask);
       // 2,主线程想要获取 异步任务的执行结果
        System.out.println(futureTask.get());
        //3,关闭线程池
        threadPool.shutdown();
    }
}

执行结果：主线程阻塞等待直至获取到结果

休眠3s结束！  
ok!

八、总结

• 1,在线程池中线程数还未达到核心线程数时，每新来一个任务就创建一个新线程，即使有空闲的线程。
• 2,线程池中不是在达到最大线程数后，再将新提交的任务放入阻塞队列中，而是在大于等于核心线程数后，就将新任务添加到阻塞队列，有些线程池虽然核心线程数等于最大线程数，但是判断对象一定是核心线程数 。
• 3,每次创建线程池，记着使用完毕，执行shutdown()方法，关闭线程池。
• 4,Java为我们提供的线程池更偏向 cpu 密集型任务场景，因为只有在加入阻塞队列失败的情况，才会去尝试创建其他非核心线程，如果我们想要处理IO密集型任务，创建多个线程来处理，又能非常高效，此处可参考Tomcat的线程池原理，她对java原生线程池做了拓展修改，以应对非常多的请求的场景（IO密集任务）。

开发中推荐使用线程池创建线程, 可减少线程的创建和销毁的时间和系统资源的开销，合理使用线程池，可节约资源，减少每次都创建线程的开销，可实现线程的重复使用。本文从线程池的内部工作原理开始介绍、以及Jdk为我们默认提供的三类线程池的特点和缺陷、线程池中常用的3种阻塞队列、以及4种拒绝策略、开发中我们推荐自定义线程池、线程池2种提交任务的方式等；在了解线程池后，开发中我们能够避免踩坑，也能有效让它为我们所用，提升开发效率，节约资源。

---

参考资料：

1、Java 并发编程的艺术 - 方腾飞

2、Java 开发手册