大厂算法面试之leetcode精讲6.深度优先&广度优先
Posted 全栈潇晨
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了大厂算法面试之leetcode精讲6.深度优先&广度优先相关的知识,希望对你有一定的参考价值。
大厂算法面试之leetcode精讲6.深度优先&广度优先
视频教程(高效学习):点击学习
目录:
深度优先&广度优先
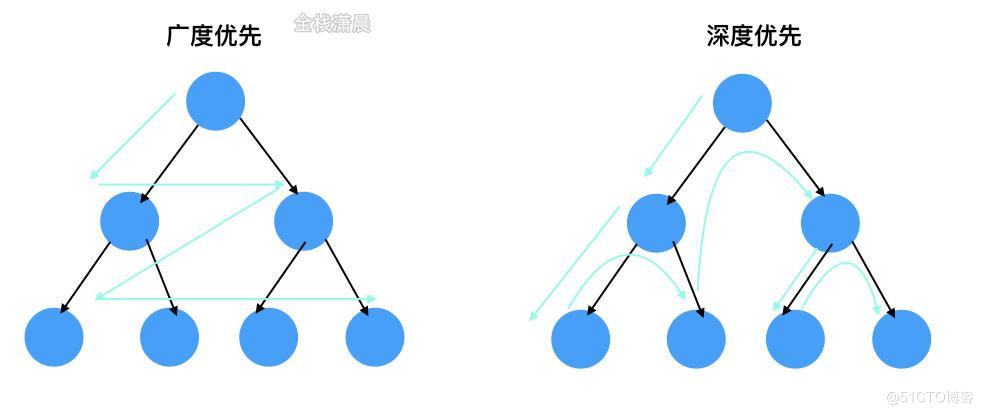
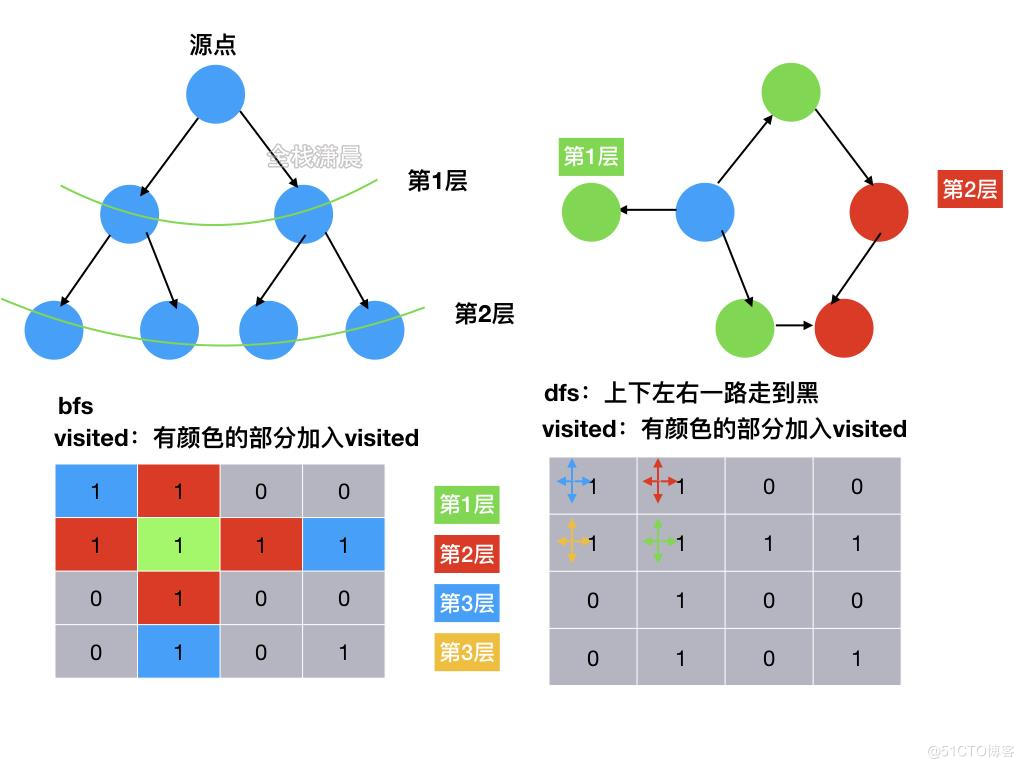
bfs:适用于层序遍历或者寻找最短路径的问。
//bfs伪代码模版
function bfs(graph, start, end) {
queue = [];
queue.append([start]);
visited.add(start);
while (queue)
node = queue.pop();
visited.add(node);
process(node);
nodes = generate_related_nodes(node);
queue.add(nodes);
}
dfs:
//dfs伪代码模版
//递归
function dfs(node, visited) {
visited.add(node);
for (next_node in node.children()) {
if (!next_node in visited)
dfs(next_node, visited);
}
}
//非递归
function dfs(tree) {
if (tree.root === null) {
return [];
}
visited, (stack = []), [tree.node];
while (stack)
node = stack.pop();
visited.add(node);
process(node);
nodes = generate_ralated_nodes(node);
stack.push(nodes);
}695. 岛屿的最大面积 (medium)
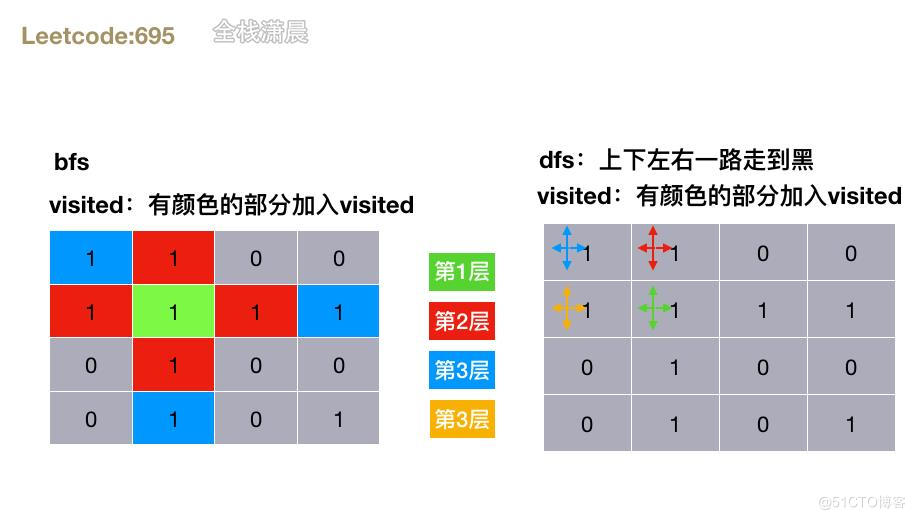
方法1.dfs
- 思路:深度优先,先循环网格, 当
grid[x][y] === 1时,将当前单元格置为0并上下左右不断递归,计算每个岛屿的大小,然后不断更新最大岛屿 - 复杂度:时间复杂度
O(mn),m、n分别是网格的长和宽。空间复杂度O(mn),递归最大深度
js:
var maxAreaOfIsland = function(grid) {
let row = grid.length, col = grid[0].length;
function dfs (x, y) {
//越界判断 当grid[x][y] === 0时 直接返回
if (x < 0 || x >= row || y < 0 || y >= col || grid[x][y] === 0) return 0;
grid[x][y] = 0;//当grid[x][y] === 1时,将当前单元格置为0
let ans = 1, dx = [-1, 1, 0, 0], dy = [0, 0, 1, -1];//方向数组
for (let i = 0; i < dx.length; i++) {//上下左右不断递归,计算每个岛屿的大小
ans += dfs(x + dx[i], y + dy[i]);
}
return ans;
}
let res = 0;
for (let i = 0; i < row; i++) {
for (let j = 0; j < col; j++) {
res = Math.max(res, dfs(i, j));//循环网格 更新最大岛屿
}
}
return res;
};
java
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == 1){
res = Math.max(res, dfs(grid, i, j));
}
}
}
return res;
}
public int dfs(int[][] grid, int i, int j){
if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == 0){
return 0;
}
grid[i][j] = 0;
return 1 + dfs(grid, i - 1, j) + dfs(grid, i + 1, j) + dfs(grid, i, j - 1) + dfs(grid, i, j + 1);
}
}
方法2.bfs
- 思路:广度优先,循环网格,不断将当前网格的坐标加入队列,如果当前网格对应的值是1,则置为0,然后向四周扩散,找到下一层的网格坐标,加入队列,直到队列为空
- 复杂度:时间复杂度
O(mn),m、n分别是网格的长和宽。空间复杂度O(mn),queue的大小
js:
var maxAreaOfIsland = function(grid) {
let ans = 0, row = grid.length, col = grid[0].length;
let dx = [1, -1, 0, 0], dy = [0, 0, 1, -1];//方向数组
for (let i = 0; i < row; i++) {
for (let j = 0; j < col; j++) {
if (grid[i][j] === 0) continue;//循环网格,遇到0就跳过
let queue = [[i, j]], curr = 0;//在队列中加入当前网格的值
while (queue.length > 0) {
let [x, y] = queue.shift();//不断出队
//越界判断
if (x < 0 || x >= row || y < 0 || y >= col || grid[x][y] === 0) continue;
++curr;//更新岛屿的数量
grid[x][y] = 0;//遍历过的网格置为0
for (let k = 0; k < dx.length; k++) {//上下左右遍历,把下一层的节点加入队列
queue.push([x + dx[k], y + dy[k]]);
}
}
ans = Math.max(ans, curr);//更新最大岛屿面积
}
}
return ans;
};
java
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == 1){
res = Math.max(res, bfs(grid, i, j));
}
}
}
return res;
}
public int bfs(int[][] grid, int i, int j){
int[] dx = {1, -1, 0, 0};
int[] dy = {0, 0, 1, -1};
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{i, j});
grid[i][j] = 0;
int area = 1;
while(!queue.isEmpty()){
int[] x = queue.poll();
for(int index = 0; index < 4; index++){
int nx = x[0] + dx[index], ny = x[1] + dy[index];
if(nx>=0 && nx < grid.length && ny >= 0 && ny < grid[0].length && grid[nx][ny] == 1){
grid[nx][ny] = 0;
area += 1;
queue.offer(new int[]{nx, ny});
}
}
}
return area;
}
}
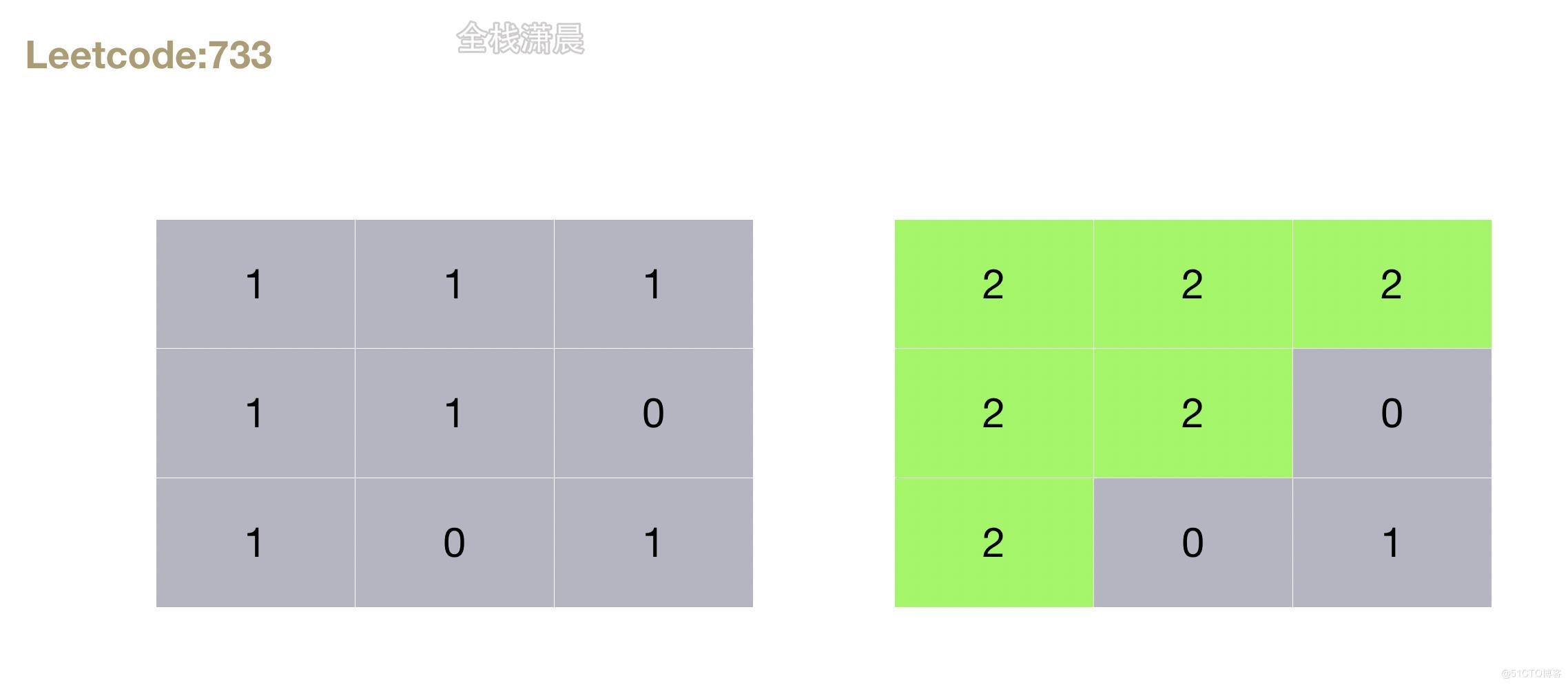
733. 图像渲染 (easy)
方法1.dfs
- 复杂度:时间复杂度
O(mn),m、n分别是网格的长和宽。空间复杂度O(mn),递归最大深度
js:
const floodFill = (image, sr, sc, newColor) => {
const m = image.length;
const n = image[0].length;
const oldColor = image[sr][sc];
if (oldColor == newColor) return image;
const fill = (i, j) => {
if (i < 0 || i >= m || j < 0 || j >= n || image[i][j] != oldColor) {
return;
}
image[i][j] = newColor;
fill(i - 1, j);
fill(i + 1, j);
fill(i, j - 1);
fill(i, j + 1);
};
fill(sr, sc);
return image;
};
方法2.bfs
- 复杂度:时间复杂度
O(mn),m、n分别是网格的长和宽。空间复杂度O(mn),递归最大深度
js:
const floodFill = (image, sr, sc, newColor) => {
const m = image.length;
const n = image[0].length;
const oldColor = image[sr][sc];
if (oldColor == newColor) return image;
const queue = [[sr, sc]];
while (queue.length) {
const [i, j] = queue.shift();
image[i][j] = newColor;
if (i - 1 >= 0 && image[i - 1][j] == oldColor) queue.push([i - 1, j]);
if (i + 1 < m && image[i + 1][j] == oldColor) queue.push([i + 1, j]);
if (j - 1 >= 0 && image[i][j - 1] == oldColor) queue.push([i, j - 1]);
if (j + 1 < n && image[i][j + 1] == oldColor) queue.push([i, j + 1]);
}
return image;
};
以上是关于大厂算法面试之leetcode精讲6.深度优先&广度优先的主要内容,如果未能解决你的问题,请参考以下文章