Sym-NCO: Leveraging Symmetricity for Neural Combinatorial Optimization 学习笔记

Posted 2023-03-12 好奇小圈

文章目录

• 摘要
• 零、一些基础
• • 1.Invariant Representation
• 一、介绍
• • • • 高性能
      • 问题不可知论
      • 架构不可知论
• 二、组合优化马尔可夫决策过程中的对称性
• • 0.基础
  • 1.组合优化马尔可夫决策过程
  • • • 状态
      • 动作
      • 奖励
  • 2.CO-MDP的对称性
  • • （0）基础
    • （1）问题对称性（定义2.1）
    • （2）解对称性（定义2.2）
    • （3）旋转对称性（定理2.1）
• 三、对称神经组合优化
• • 1.通过${\mathcal{L}}_{\mathrm{inv}}$进行不变问题表示
  • 2.通过${\mathcal{L}}_{\mathrm{ps}}$和${\mathcal{L}}_{\mathrm{ss}}$强加问题和解的对称性
  • • （0）基础
    • （1）施加解决方案对称性
    • （2）施加问题和解决方案对称性
• 四、相关工作
• • 1.深部构造启发式
  • 2.等变深度学习
• 五、实验
• • 0.基础
  • 1.任务和基线选择
  • 2.实验设置
  • • • 问题尺寸
      • 超参数
      • 数据集和计算资源
  • 3.性能标准
  • • • 平均成本
      • 评估速度
      • 贪婪/多启动性能
  • 4.实验结果
  • • （1）TSP和CVRP的结果
    • （2）PCTSP和OP的结果
    • （3）real-world TSP的结果
    • （4）应用于各种DRL-NCO方法
    • （5）多起点的时间性能分析
• 六、讨论
• • 1.软不变学习vs.硬约束不变学习
  • • （0）基础
    • （1）${\mathcal{L}}_{inv}$的消融研究
    • （2）与EGNN的比较
  • 2.限制和未来的方向
  • • （1）扩展问题对称性
    • （2）大尺度适应
    • （3）对图形COP的扩展
• 七、附录
• • A 定理2.1的证明
  • B 基线的实施
  • • B.1 指针网络
    • B.2 AM
    • B.3 POMO
  • C 有能力的车辆路径规划问题
  • • C.1 训练超参数
    • C.2 多起点 后处理
    • C.3 投影头的细节
    • C.4 计算资源和计算时间
• 八、主要参考文献
• 九、代码解析
• 相关领域

---

摘要

基于深度强化学习（DRL）的组合优化（CO）方法（如DRL-NCO）已经展现了超过传统CO解决器的显著优点，因为DRL-NCO能够在没有验证求解器得到监督的情况下学习CO求解器标签。本文展示了一个新的训练方案，Sym-NCO，与现有DRL-NCO方法的性能显著提高。Sym-NCO是一种基于正则化器的训练方案，它在各种CO问题和解决方案中利用了通用的对称性。施加旋转不变性和反射不变性等对称性可以大大提高DRL-NCO的泛化能力，因为对称性是某些CO任务所共享的不变性特征。我们的实验结果验证了我们的Sym-NCO大大提高了DRL-NCO方法在四种CO任务中的性能，包括旅行推销员问题（TSP）、能力有限的车辆路径问题（CVRP）、奖品收集TSP（PCTSP）、定向问题（OP），没有使用特定问题的技术。值得注意的是，Sym-NCO不仅优于现有的DRL-NCO方法，而且优于具有竞争力的传统求解器迭代局部搜索（ILS），在PCTSP中有240倍的更快速度。

---

零、一些基础

1.Invariant Representation

不变表示（invariant representation）是一种计算机编程中的概念，指的是一组不受对象状态影响的恒定属性。不变表示可以用于域自适应（domain adaptation）或强化学习（reinforcement learning）等领域，以提高学习效率和泛化能力。不变表示也可以通过相对于一个基准帧（basis frame）来描述所有帧的配置来实现结构的全局位置和方向的不变性。

一、介绍

组合优化问题（COPs）是离散输入空间上的数学优化问题，具有许多有价值的应用价值，包括车辆路由问题（VRPs）、药物发现和半导体芯片设计。然而，由于COP的NP-hard，很难找到一个最优的解决方案。因此，从实际的角度来看，快速计算接近最优的解是必要的。

传统上，COPs是通过整数程序（IP）求解器或手工制作的（meta）启发式方法来解决的。计算基础设施和深度学习的最新进展构思了神经组合优化（NCO）领域，这是一种基于深度学习的COP解决策略。根据训练方案的不同，NCO方法通常分为监督学习和强化学习（RL）。根据解生成方案的不同，NCO方法也被分为改进式和构造启发式。在NCO方法中，基于深度RL（DRL）的建设性启发式（即DRL-NCO）优于传统方法，因为RL的训练能力不依赖于现有的COP解决方案，以及易处理的构造过程，该过程防止违反规则的特定任务，并保证合格的解决方案。

尽管DRL-NCO很强大，但最先进的常规启发式与DRL-NCO之间存在性能差距。为了缩小差距，已经有人尝试对现有的DRL-NCO方法采用特定问题的启发式。然而，设计一个通用的训练方案来提高DRL-NCO的性能仍然具有挑战性。

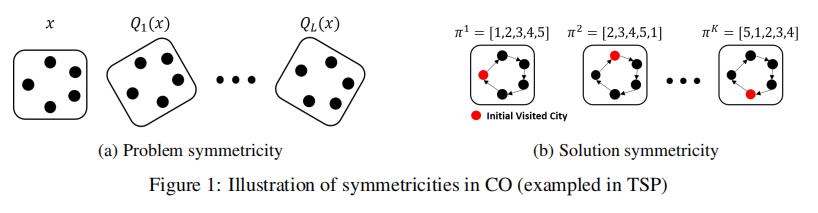
在本研究中，我们提出了对称神经组合优化（Sym-NCO），这是一种适用于通用CO问题的通用训练方案。Sym-NCO是一种基于正则化的训练方案，它利用COPs中常见的对称性来提高现有的DRL-NCO方法的性能。为此，我们首先确定了各种COPs中存在的对称性。Sym-NCO利用了在欧几里得图上定义的COP中固有的两种对称性。首先，由解的旋转不变性推导出的问题的对称性；旋转图必须表现出与原始图相同的最优解，如图1a所示。其次是解的对称性，即具有相同最优值的解之间的共享特征。例如，旅行推销员问题（TSP）中的解对称性包括了第一城市的排列不变性（见图1b）。然而，在训练过程中必须自动识别一般COPs的解对称性。这是因为在没有高度研究的领域知识的情况下，多个最优解之间的共享特征通常是难以处理的。

Sym-NCO由两种新的利用对称性的正则化方法组成。首先，我们提出了一种新的优势REINFORCE算法函数，它可以自动识别和利用对称性，而不施加误导性偏差。其次，我们设计了一种新的表示学习方案，通过利用预先识别的对称性来施加对称性。

我们在各种现有的DRL-NCO方法上实验验证了Sym-NCO，通过解决它们的原始目标问题，而没有使用任何特定于问题的技术。通过利用COPs的对称性，Sym-NCO实现了以下目标：

高性能

Sym-NCO在各种COP任务中以极高的速度（解决10,000个实例的几秒钟）实现了接近最佳的性能（不到2%）。此外，SymNCO以更快240×的速度超过了竞争激烈的PCTSP求解器ILS 。

问题不可知论

Sym-NCO不使用特定于问题的启发式方法来解决各种COPs。Sym-NCO一般适用于TSP、CVRP PCTSP和OP的解决方案。

架构不可知论

Sym-NCO可以很容易地实现到任何编码器-解码器模型上，并施加COPs的对称性。Sym-NCO成功地提高了现有的基于编码器-解码器的DRL-NCO方法的性能，如指针网络、AM和POMO。

二、组合优化马尔可夫决策过程中的对称性

0.基础

本节介绍了在组合优化中发现的几个对称特征，并在马尔可夫决策过程中加以表述。NCO的目标是通过解决以下问题来训练$\theta$参数化求解器$F_{\theta }$，如式（1）：
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmax}}{\mathbb{E}}_{\mathbf{P}\sim \rho }\left[{\mathbb{E}}_{\mathbf{\pi }(\mathbf{P})\sim F_{\theta }(\mathbf{P})}[R(\mathbf{\pi }(\mathbf{P}))]\right]$$
其中$\mathbf{P}=(\mathbf{x},\mathbf{f})$是有$N$个节点的问题实例，由节点坐标$\mathbf{x}={x_i}_{i=1}^N$和相关$N$个特征$\mathbf{f}={x_i}_{i=1}^N$组成。
$\rho$是问题生成分布，
$\mathbf{\pi }(\mathbf{P})$是$\mathbf{P}$的解决方案，
$R(\mathbf{\pi }(\mathbf{P}))$是$\mathbf{\pi }(\mathbf{P})$的目标价值。

1.组合优化马尔可夫决策过程

我们将组合优化马尔可夫决策过程（CO-MDP）定义为COP解的顺序构造。对于一个给定的$\mathbf{P}$，相应的CO-MDP的分量定义如下：

状态

状态${\mathbf{s}}_t=\left({\mathbf{a}}_{1:t},\mathbf{x},\mathbf{f}\right)$是第$t$（部分完成）解决方案，其中${\mathbf{a}}_{1:t}$表示之前选择的节点。初始状态和终端状态$s_0$和$s_T$分别等价于空解和完成解。在本文中，我们将解$\mathbf{\pi }(\mathbf{P})$表示为完全解。

动作

动作$a_t$是从未访问节点中选择一个节点（即$a_t\in {\mathbb{A}}_t=1,\dots ,N\backslash \backslash {\mathbf{a}}_{1:t-1}$）

奖励

奖励$R(\mathbf{\pi }(\mathbf{P}))$是COP的目标。我们假定奖励是${\mathbf{a}}_{1:T}$（解序列）的函数，${\Vert x_i-x_j\Vert }_{i,j\in 1,\dots N}$（相对距离）和$\mathbf{f}$（节点特征）。在TSP，能力受限的VRP（CVRP）和奖励收集TSPs（PCTSP），奖励是旅途长度的负数。在定向运动问题（OP）奖励是价值的总和。

当定义CO-MDP时，我们可以定义解地图为式（2）：
$$\pi (P)\sim F_{\theta }(P)=\prod _{t=1}^T{p}_{\theta }\left(a_t\mid s_t(P)\right)$$
其中$p_{\theta }\left(a_t\mid {\mathbf{s}}_t(\mathbf{P})\right)$是策略，用于在状态$s_t$产生$a^{}$