数据挖掘实战——应用系统负载分析与容量预测(ARIMA模型)
Posted Lingxw_w
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据挖掘实战——应用系统负载分析与容量预测(ARIMA模型)相关的知识,希望对你有一定的参考价值。

项目地址:Datamining_project: 数据挖掘实战项目代码
目录
一、背景和挖掘目标
1、问题背景
应用系统是由服务器、数据库、中间件、存储设备等组成。它在日常运行时,会对底层软硬件造成负荷。其中任何一种资源负载过大,都可能会引起应用系统性能下降甚至瘫痪。及时了解当前应用系统的负载情况,以便提前预防,确保系统安全稳定运行。- 应用系统的负载率:通过对一段时间内软硬件性能的运行状况进行综合评分而获得。
- 负载率趋势:通过系统的当前负载率与历史平均负载率进行比较。
2、传统方法的不足
系统负载分析的传统方法:通过监控采集到的性能数据以及所发出的告警事件,人为进行判断系统的负载情况。此方法虽然能够判断系统故障以及磁盘的容量情况,但是存在一些缺陷和不足:- 磁盘容量的情况没有提供预测的功能。只有当容量将要被耗尽时,会有告警提示。如果是告警服务器的磁盘容量被耗尽,此种情况下,系统即使出现故障,也不会有告警提示。
- 不能提前知道系统负载的程度,只有当系统故障时,通过接受告警才得知。并且当系统真正故障的时,告警的发出大多数情况下会有一定的延迟。
2、原始数据
- 性能属性说明:针对采集的性能信息,对每个属性进行相应说明。
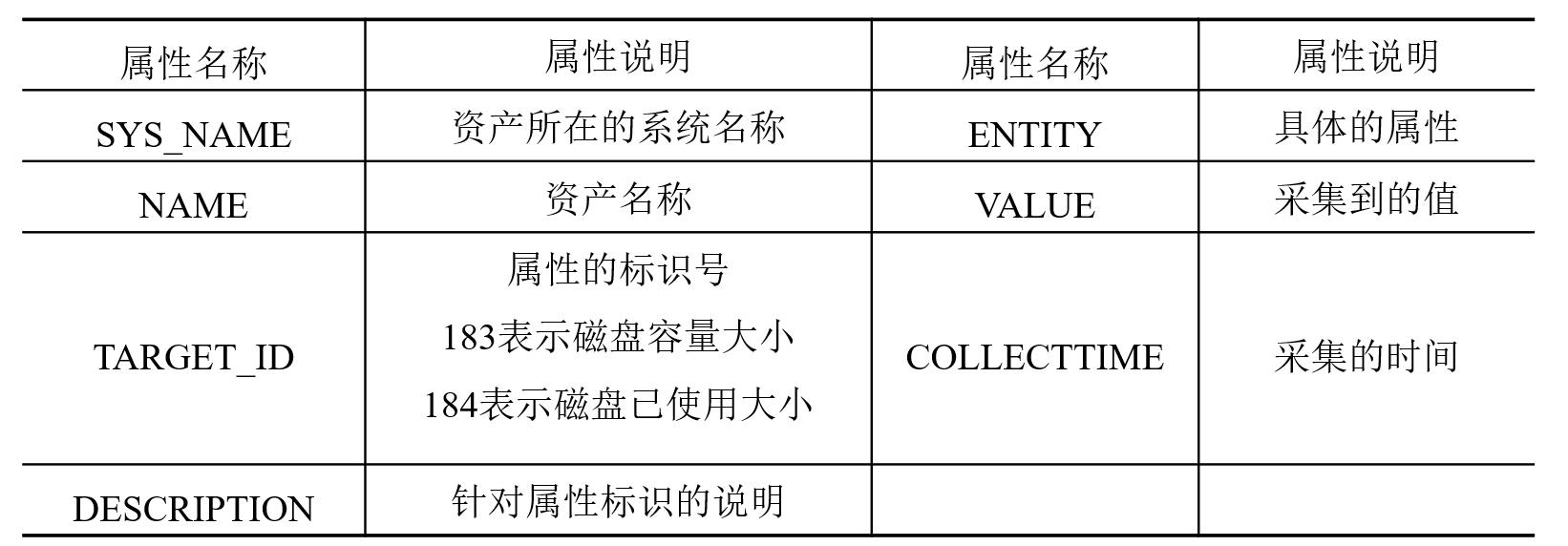
- 磁盘数据:包含应用系统、磁盘基本信息等。
3、挖掘目标
- 针对历史磁盘数据,采用数据挖掘的方法,预测应用系统服务器磁盘已使用空间大小;
- 根据用户需求设置不同的预警等级,将预测值与容量值进行比较,对其结果进行预警判断,为系统管理员提供定制化的预警提示;
二、分析方法与过程
1、初步分析
- 应用系统出现故障通常不是突然瘫痪造成的(除非对服务器直接断电),而是一个渐变的过程。例如系统长时间运行,数据会持续写入存储,存储空间逐渐变少,最终磁盘被写满而导致系统故障。
- 在不考虑人为因素的影响时,存储空间随时间变化存在很强的关联性,且历史数据对未来的发展存在一定的影响,故可采用时间序列分析法对磁盘已使用空间进行预测分析。
2、总体流程
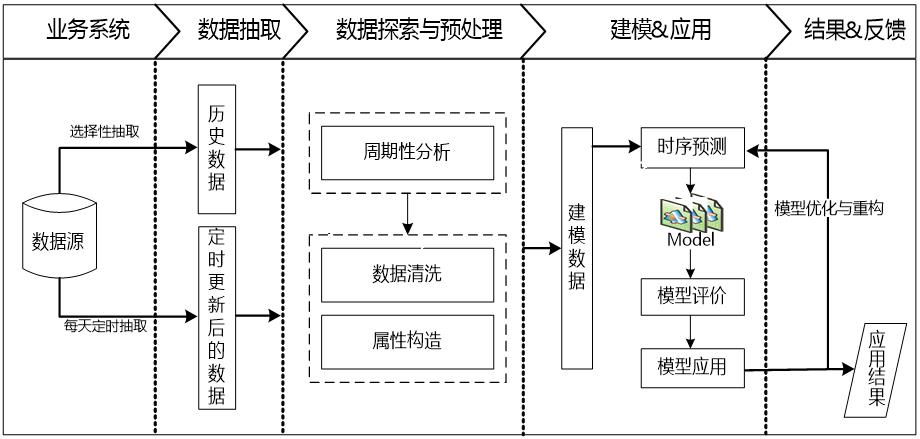
第一步:数据抽取
磁盘使用情况的数据都存放在性能数据中,而监控采集的性能数据中存在大量的其他属性数据。故以属性的标识号(TARGET_ID)与采集指标的时间(COLLECTTIME)为条件,对性能数据进行抽取。
抽取10-01至11-16财务管理系统中某一台数据库服务器的磁盘的相关数据。第二步:探索分析
对数据进行周期性分析,探索数据的平稳性。
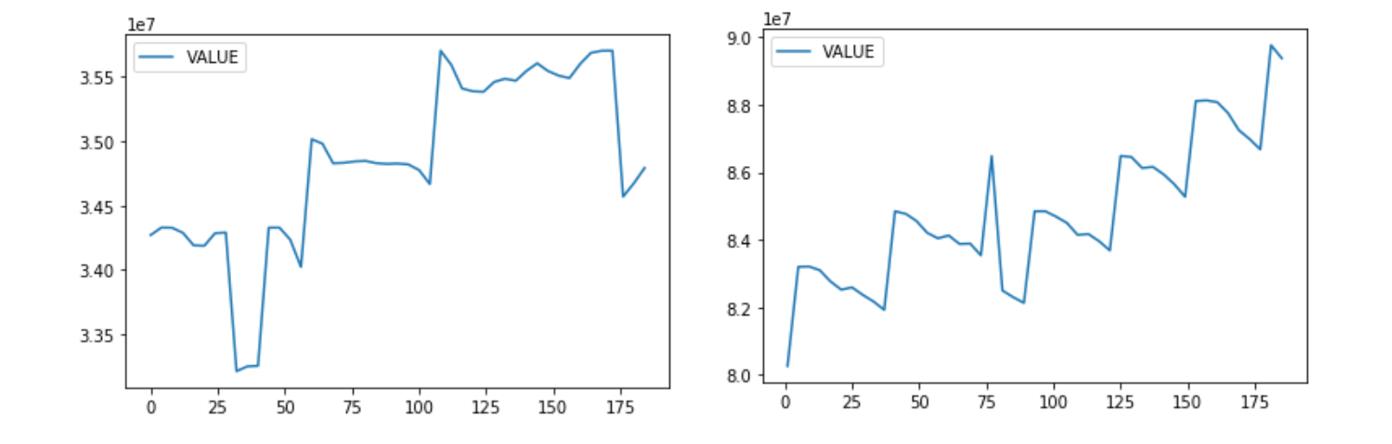
C盘和D盘的使用的大小。
# -*- coding:utf-8 -*-
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_excel('data/discdata.xls')
str1 = 'C:\\\\'
str2 = 'D:\\\\'
dataC = data[(data['DESCRIPTION'] == '磁盘已使用大小') & (data['ENTITY'] == str1)]
dataD = data[(data['DESCRIPTION'] == '磁盘已使用大小') & (data['ENTITY'] == str2)]
dataC.plot(y='VALUE')
dataD.plot(y='VALUE')
plt.show()第三步:数据的预处理
数据清洗:实际业务中,监控系统会每天定时对磁盘的信息进行收集,但是磁盘容量属性一般情况下都是一个定值(不考虑中途扩容的情况),因此磁盘原始数据中会存在磁盘容量的重复数据。
- 剔除磁盘容量的重复数据。
- 将所有服务器的磁盘容量作为一个固定值,方便模型预警时需要。
 属性构造:因每台服务器的磁盘信息可以通过表中NAME,TARGET_ID,ENTITY三个属性进行区分,且每台服务器的上述三个属性值是不变的,所以可以将三个属性的值进行合并。 (实质是将行转换成列)。
属性构造:因每台服务器的磁盘信息可以通过表中NAME,TARGET_ID,ENTITY三个属性进行区分,且每台服务器的上述三个属性值是不变的,所以可以将三个属性的值进行合并。 (实质是将行转换成列)。

# -*-coding: utf-8-*-
import pandas as pd
def attr_trans(x):
result = pd.Series(index=['SYS_NAME', 'CWXT_DB:184:C:\\\\', 'CWXT_DB:184:D:\\\\', 'COLLECTTIME'])
result['SYS_NAME'] = x['SYS_NAME'].iloc[0]
result['COLLECTTIME'] = x['COLLECTTIME'].iloc[0]
result['CWXT_DB:184:C:\\\\'] = x['VALUE'].iloc[0]
result['CWXT_DB:184:D:\\\\'] = x['VALUE'].iloc[1]
return result
discfile = 'data/discdata.xls'
transformeddata = 'data/discdata_processed.xls'
data = pd.read_excel(discfile)
data = data[data['TARGET_ID'] == 184].copy()
# 按时间分组
data_group = data.groupby('COLLECTTIME')
data_processed = data_group.apply(attr_trans)
data_processed.to_excel(transformeddata, index=False)3、构造容量预测模型
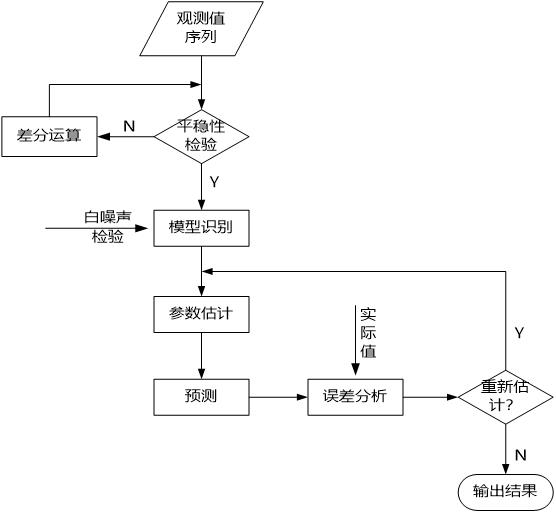
- 平稳性检验:为了确定原始数据序列中没有随机趋势或趋势,需要对数据进行平稳性检验,否则将会产生“伪回归”的现象。方法:单位跟检验或者观察时序图。
- 白噪声检验:为了验证序列中有用的信息是否已被提取完毕,需要对序列进行白噪声检验。如果序列检验为白噪声序列,就说明序列中有用的信息已经被提取完毕了,剩下的全是随机扰动,无法进行预测和使用。方法:一般采用LB统计量检验方法。
- 模型识别:通过AIC、BIC信息准则或者观测自相关图和偏自相关图确定P、Q的参数,识别其模型属于AR、MA和ARMA中的哪一种模型。
- 参数估计:估计模型的其他参数。可以采用极大似然估计、条件最小二乘法确定。
- 模型检验:检测模型残差序列是否属于白噪声序列。

# -*- coding:utf-8 -*-
import pandas as pd
def stationarityTest():
'''
平稳性检验
:return:
'''
discfile = 'data/discdata_processed.xls'
predictnum = 5
data = pd.read_excel(discfile)
data = data.iloc[: len(data) - predictnum]
# 平稳性检验
from statsmodels.tsa.stattools import adfuller as ADF
diff = 0
adf = ADF(data['CWXT_DB:184:D:\\\\'])
while adf[1] > 0.05:
diff = diff + 1
adf = ADF(data['CWXT_DB:184:D:\\\\'].diff(diff).dropna())
print(u'原始序列经过%s阶差分后归于平稳,p值为%s' % (diff, adf[1]))
def whitenoiseTest():
'''
白噪声检验
:return:
'''
discfile = 'data/discdata_processed.xls'
data = pd.read_excel(discfile)
data = data.iloc[: len(data) - 5]
# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
[[lb], [p]] = acorr_ljungbox(data['CWXT_DB:184:D:\\\\'], lags=1)
if p < 0.05:
print(u'原始序列为非白噪声序列,对应的p值为:%s' % p)
else:
print(u'原始该序列为白噪声序列,对应的p值为:%s' % p)
[[lb], [p]] = acorr_ljungbox(data['CWXT_DB:184:D:\\\\'].diff().dropna(), lags=1)
if p < 0.05:
print(u'一阶差分序列为非白噪声序列,对应的p值为:%s' % p)
else:
print(u'一阶差分该序列为白噪声序列,对应的p值为:%s' % p)
def findOptimalpq():
'''
得到模型参数
:return:
'''
discfile = 'data/discdata_processed.xls'
data = pd.read_excel(discfile, index_col='COLLECTTIME')
data = data.iloc[: len(data) - 5]
xdata = data['CWXT_DB:184:D:\\\\']
from statsmodels.tsa.arima_model import ARIMA
# 定阶
# 一般阶数不超过length/10
pmax = int(len(xdata) / 10)
qmax = int(len(xdata) / 10)
# bic矩阵
bic_matrix = []
for p in range(pmax + 1):
tmp = []
for q in range(qmax + 1):
try:
tmp.append(ARIMA(xdata, (p, 1, q)).fit().bic)
except:
tmp.append(None)
bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix)
# 先用stack展平,然后用idxmin找出最小值位置。
p, q = bic_matrix.stack().astype('float64').idxmin()
print(u'BIC最小的p值和q值为:%s、%s' % (p, q))
def arimaModelCheck():
'''
模型检验
:return:
'''
discfile = 'data/discdata_processed.xls'
# 残差延迟个数
lagnum = 12
data = pd.read_excel(discfile, index_col='COLLECTTIME')
data = data.iloc[: len(data) - 5]
xdata = data['CWXT_DB:184:D:\\\\']
# 建立ARIMA(0,1,1)模型
from statsmodels.tsa.arima_model import ARIMA
# 建立并训练模型
arima = ARIMA(xdata, (0, 1, 1)).fit()
# 预测
xdata_pred = arima.predict(typ='levels')
# 计算残差
pred_error = (xdata_pred - xdata).dropna()
from statsmodels.stats.diagnostic import acorr_ljungbox
# 白噪声检验
lb, p = acorr_ljungbox(pred_error, lags=lagnum)
# p值小于0.05,认为是非白噪声。
h = (p < 0.05).sum()
if h > 0:
print(u'模型ARIMA(0,1,1)不符合白噪声检验')
else:
print(u'模型ARIMA(0,1,1)符合白噪声检验')
def calErrors():
'''
误差计算
:return:
'''
# 参数初始化
file = 'data/predictdata.xls'
data = pd.read_excel(file)
# 计算误差
abs_ = (data[u'预测值'] - data[u'实际值']).abs()
mae_ = abs_.mean() # mae
rmse_ = ((abs_ ** 2).mean()) ** 0.5
mape_ = (abs_ / data[u'实际值']).mean()
print(u'平均绝对误差为:%0.4f,\\n均方根误差为:%0.4f,\\n平均绝对百分误差为:%0.6f。' % (mae_, rmse_, mape_))
stationarityTest()
whitenoiseTest()
findOptimalpq()
arimaModelCheck()
calErrors()
模型预测:应用模型进行预测,获取未来5天的预测值。为了方便比较,将单位换算成GB。
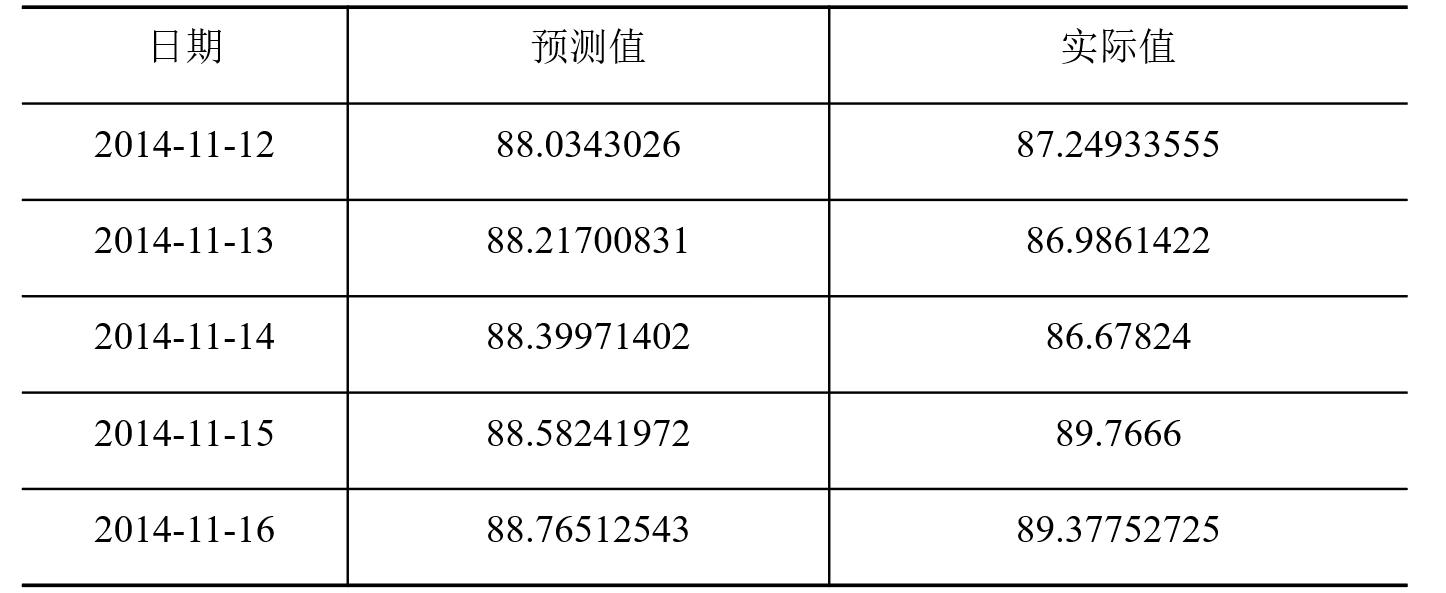
模型评价:
采用三个衡量模型预测精度的统计量指标:平均绝对误差、均方根误差、平均绝对百分误差,从不同侧面反映了算法的预测精度。

模型应用:
- 计算预测使用率:根据模型预测得到的值,计算预测使用率。
- 设定预警等级:根据业务应用一般设置的阈值,也可以根据管理员要求进行相应的调整。
- 发布预警信息

三、总结和思考
- 监控不仅能够获取软硬件的性能数据,同时也能检测到软硬件的日志事件,并通过告警的方式提示用户。因此管理员在维护系统的过程中,特别关注应用系统类别的告警。一旦系统发生故障,则会影响整个公司的运作。但是在监控收集性能以及事件的过程中,会存在各类型告警误告情况。(注:应用系统发生误告时系统实际处于正常阶段)
- 根据历史每天的各种类型的告警数,通过相关性进行检验判断哪些类型告警与应用系统真正故障有关。通过相关类型的告警,预测明后两天的告警数。针对历史的告警数与应用系统的关系,判断系统未来是否发生故障。
- 可通过时序算法预测未来相关类型的告警数,然后采用分类预测算法对预测值进行判断,判断系统未来是否发生故障。
以上是关于数据挖掘实战——应用系统负载分析与容量预测(ARIMA模型)的主要内容,如果未能解决你的问题,请参考以下文章