简介
AMQ(approximate membership queries近似成员查询):
- 是一种字典数据结构
- 是在空间使用和查询错误率的权衡
- 用于解决大量数据的处理
- 拥有以下操作
- 查找
- 插入
- 可选择元素的删除
- 设e误检率,当查询时报出absent值时,e的概率为误检,1-e的概率为确实没有该元素。
- 可以通过调整e值来调整准确度和空间使用的关系
举例
Bloom Filter
Bloom filter
- Bloom Filter(BF)是一种空间效率很高的随机数据结构,它利用位数组很简洁地表示一个集合
- 历史:Bloom-Filter,即布隆过滤器,1970年由Bloom中提出。
- 应用:用于检索一个元素是否在一个集合中。
- 特点:Bloom Filter有可能会出现错误判断,但不会漏掉判断。
- 适用场景:Bloom Filter”不适合那些“零错误的应用场合。而在能容忍低错误率的应用场合下,Bloom Filter比其他常见的算法(如hash,折半查找)极大节省了空间。
- 优点:是空间效率和查询时间都远远超过一般的算法,
- 缺点:是有一定的误识别率和删除困难。
算法过程
- 原理要点:一是位数组, 二是k个独立hash函数。
1)位数组:

- 假设Bloom Filter使用一个m比特的数组来保存信息,初始状态时,Bloom Filter是一个包含m位的位数组,每一位都置为0,即BF整个数组的元素都设置为0。
2)添加元素,k个独立hash函数
-
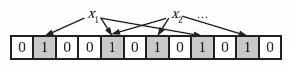
为了表达S={x1, x2,…,xn}这样一个n个元素的集合,Bloom Filter使用k个相互独立的哈希函数(Hash Function),它们分别将集合中的每个元素映射到{1,…,m}的范围中。
-
当我们往Bloom Filter中增加任意一个元素x时候,我们使用k个哈希函数得到k个哈希值,然后将数组中对应的比特位设置为1。即第i个哈希函数映射的位置hashi(x)就会被置为1(1≤i≤k)。
-
注意,如果一个位置多次被置为1,那么只有第一次会起作用,后面几次将没有任何效果。在下图中,k=3,且有两个哈希函数选中同一个位置(从左边数第五位,即第二个“1“处)。
3)判断元素是否存在集合
-
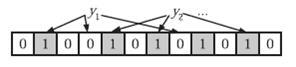
在判断y是否属于这个集合时,我们只需要对y使用k个哈希函数得到k个哈希值,如果所有hashi(y)的位置都是1(1≤i≤k),即k个位置都被设置为1了,那么我们就认为y是集合中的元素,否则就认为y不是集合中的元素。下图中y1就不是集合中的元素(因为y1有一处指向了“0”位)。y2或者属于这个集合,或者刚好是一个false positive。
-
显然这个判断并不保证查找的结果是100%正确的。
Quotient Filter and Cascade Filter
- Quitient Filter 和Cascade Filter算法由Bender等人设计,是一个空间效率高的概率性数据结构
- 应用:用于检索一个元素是否在一个集合中。
- 优点:对插入、查询、删除操作由高吞吐量,比Bloom Filter高了两个数量级。
- 更多详情见[3][4]
参考文献
[1] https://www.cnblogs.com/zhxshseu/p/5289871.html
[2] https://en.wikipedia.org/wiki/Bloom_filter
[3] https://en.wikipedia.org/wiki/Quotient_filter
[4] Don’t Thrash: How to Cache your Hash on Flash