初级程序员软考重点1 计算机内数据表示及编码基础
Posted 编程圈子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了初级程序员软考重点1 计算机内数据表示及编码基础相关的知识,希望对你有一定的参考价值。
初级程序员软考重点1 计算机内数据表示
一、二进制计算
1. 二进制转十进制整数计算
每位的数据*2的次方 值相加即可。
例:
1101 计算十进制:
1101
b
=
1
∗
2
3
+
1
∗
2
2
+
0
∗
2
1
+
1
∗
2
0
=
13
1101b = 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0 = 13
1101b=1∗23+1∗22+0∗21+1∗20=13
2. 十进制整数转二进制
除二取余法,例:42转二进制:
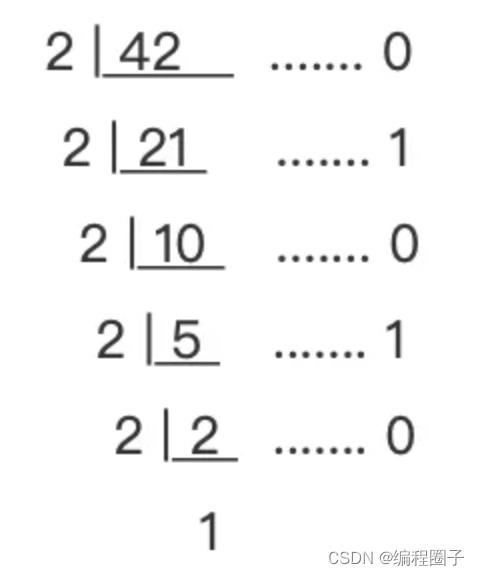
结果倒序组装: 101010b
二、原码、反码、补码、移码
- 正数的原码、反码、补码都保持不变。
- 正负0的表示: 原码、反码有两个0,补码、移码的0是唯一的。
- 计算0-0时,使用补码最好算。计算 0 + ( − 0 ) 0+(-0) 0+(−0)
1. 原码
计算机内保存数据的时候,可能会对数据进行处理。原始数据就是原码。
2. 反码
正数的反码和自身一样,负数反码是将原码除符号位各位求反。
3. 补码
正数的补码和自身一样,负数补码是对原码求反码后再加1。注意:
- 补码中 数值0的值是唯一的。
- 补码运算中,符号位与数值位采用同样的运算规则进行运算;符号位相加如果进位 , 则舍去进位。
4. 移码
偏移2n-1的情况下,移码就是将补码符号位求反。
5. 特殊数值
-127
[
−
127
]
原
=
11111111
[-127]_原=11111111
[−127]原=11111111
[
−
127
]
反
=
1000000
[-127]_反=1000000
[−127]反=1000000
[
−
127
]
补
=
1000001
[-127]_补=1000001
[−127]补=1000001
[
−
127
]
移
=
0000001
[-127]_移=0000001
[−127]移=0000001
-1
[
−
1
]
原
=
1000001
[-1]_原=1000001
[−1]原=1000001
[
−
1
]
反
=
11111110
[-1]_反=11111110
[−1]反=11111110
[
−
1
]
补
=
11111111
[-1]_补=11111111
[−1]补=11111111
[
−
1
]
移
=
01111111
[-1]_移=01111111
[−1]移=01111111
6. 表示范围
| 码制 | 定点整数最小值 | 定点整数最大值 |
|---|---|---|
| 原码 | − ( 2 n − 1 − 1 ) -(2^n-1-1) −(2n−1−1) | + ( 2 n − 1 − 1 ) +(2^n-1-1) +(2n−1−1) |
| 反码 | − ( 2 n − 1 − 1 ) -(2^n-1-1) −(2n−1−1) | + ( 2 n − 1 − 1 ) +(2^n-1-1) +(2n−1−1) |
| 补码 | − 2 n − 1 -2^n-1 −2n−1 | + ( 2 n − 1 − 1 ) +(2^n-1-1) +(2n−1−1) |
| 移码 | − 2 n − 1 -2^n-1 −2n−1 | + ( 2 n − 1 − 1 ) +(2^n-1-1) +(2n−1−1) |
三、浮点数
1. 阶码与尾数
(1)浮点数的表示 :
N = 尾 数 ∗ 基 数 指 数 N=尾数*基数^指数 N=尾数∗基数指数
N = 数 符 ∗ 尾 数 m ∗ 2 阶 符 ∗ 阶 码 e N=数符*尾数m*2^阶符*阶码e N=数符∗尾数m∗2阶符∗阶码e
(2)存储方式 :
| 阶符 | 阶码e | 数符 | 尾数m |
|---|
(3)特点
- 阶码的位数决定数的表示范围,位数越多范围越大;
- 尾数的位数决定数的有效精度,位数越多精度越高
IEEE754标准提供了两种规格的浮点格式:32位单精度格式和64位双精度格式。
32位单精度格式
| 1位 | 8位 | 23位 |
|---|---|---|
| 符号 | 阶码 | 尾数 |
64位双精度格式
| 1位 | 11位 | 52位 |
|---|---|---|
| 符号 | 阶码 | 尾数 |
其中:
- 符号位: 1表示负数,0表示正数
- 尾数:使用原码表示,规格化尾数的第一位总是1,所以1是省略的。
- 阶码:使用移码表示,偏置常数为 2 n − 1 − 1 2^n-1-1 2n−1−1
2. 示例: +178.125基于 IEEE 754标准规格化表示
(1) 转二进制
[ + 178.125 ] 10 = [ 10110010.001 ] 2 [+178.125]_10 = [10110010.001]_2 [+178.125]10=[10110010.001]2
(2) 构造尾数
将10110010.001的小数点向左移7位,去掉头部的1,尾数部分补足23位:
01100100010000000000000
(3) 构造阶码
IEEE 754规定8位阶码的偏移量为127,加上偏移量后转二进制。
上一步尾数左移了7位,127+7=254,
[
254
]
1
0
=
[
10000110
]
2
[254]_10 = [10000110]_2
[254]10=[10000110]2
(4) 符号位: 0
(5) 组合结果
0 10000110 01100100010000000000000
3. 对阶
- 在对浮点数进行加、减运算时,要先进行对阶,
- 对阶的规则是:小阶向大阶看齐;
- 阶码小的尾数右移,每右移一位、阶码加1,直到两数阶码相等。
4. 浮点数加减运算过程
- 对阶
- 尾数计算
- 结果格式化
5. 浮点数转二进制
-37/64采用8位定点机器码表示
- 转成分数形式
- 分子转成二进制
- 分子部分尾数右移
- 添加符号位
- 补足位数
四、编码基础
1. 海明码
基本知识
海明码可以进行检错和纠错。海明码在原数据中的一些固定位置插入数据,以进行奇偶校检,能更正一个比特的错误;两个比特出错时,只能侦测不能更正;三个以上比特出错,则不能侦测和纠错。
海明码校验位长度:
- 2-4位:3位校验位
- 5-11位:4位校验位
示例
对0100 1101进行海明码编码,下面P表示校验位,R表示数据位:
(1) 数据和校验位填充,校验位在P1 P2 P4 P8处
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | P4 | 1 | 1 | 0 | P3 | 1 | P2 | P1 |
(2) 计算校验位值
计算P1:从右边第1位开始把间隔1位的比特位取出来,数1数量。上表中可数得:
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | P4 | 1 | 1 | 0 | P3 | 1 | P2 | P1 |
1数量为3奇数,进行偶校验,把P1填 1。
计算P2:从右边第2位开始隔2划2:
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | P4 | 1 | 1 | 0 | P3 | 1 | P2 | P1 |
1数量为偶数,P2填0。
计算P3:从右边第4位隔4划4:
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | P4 | 1 | 1 | 0 | P3 | 1 | P2 | P1 |
1的数量为偶数,P3=0。
计算P4:从右边第8位隔8划8:
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | P4 | 1 | 1 | 0 | P3 | 1 | P2 | P1 |
计算得P4=1
编码结果:
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
侦测和更正
(1) 侦测校验位
将上面数据位错误的数据:
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
从右侧P1开始,隔1取1计算1的数量,偶数个即为正确
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
从右侧P2开始,隔2取2,1为奇数个,校验不通过
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
从右侧P4开始,隔4取4,1为奇数个,校验不通过
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
从右侧P8开始,隔8取8,1为奇数个,校验通过
| 海明码位置 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幂 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
(2) 确定出错位置
P2,P4校验不通过,2+4=6,可知第6位错误。
(3) 纠正
第6个取反即为正确数据。
2. 循环冗余校验码
循环冗余校验码(CRC)利用生成多项式为k个数据位产生r个校验位来进行编码,其编码长度为
k
+
r
k+r
k+r。
CRC由两部分组成,左边为数据,右边为校验码。如果数据占k位,则校验占n-k位。
这里n是CRC码的字长,所以又被称为(n,k)码。
求CRC编码时,采用的模2运算。
3. 哈夫曼树
构造哈夫曼树过程:
假设n个权值为w1, w2, ……, wn,准备构造的哈夫曼树有n个叶子节点,其构造规则:
从森林里选出权值最小结点合并,作为一棵新树的子树,且新权的根结点权值为其子树根节点权值之和;
从森林里删除选取的两棵树,将新树加入森林;
重复上面步骤。
示例
| 结点 | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 权值 | 0.19 | 0.05 | 0.23 | 0.13 | 0.34 | 0.06 |
构造的哈夫曼树:
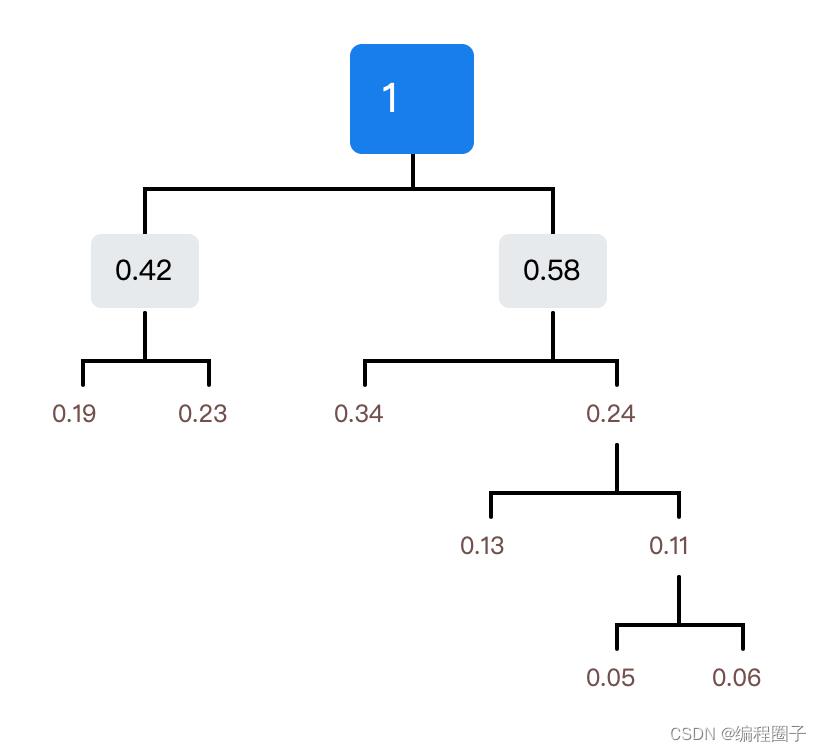
以上是关于初级程序员软考重点1 计算机内数据表示及编码基础的主要内容,如果未能解决你的问题,请参考以下文章