Bagging（Bootstrap aggregating）随机森林（random forests）AdaBoost

Posted 2020-07-13 Xurtle

引言

在这篇文章中，我会详细地介绍Bagging、随机森林和AdaBoost算法的实现，并比较它们之间的优缺点，并用scikit-learn分别实现了这3种算法来拟合Wine数据集。全篇文章伴随着实例，由浅入深，看过这篇文章以后，相信大家一定对ensemble的这些方法有了很清晰地了解。

Bagging

bagging能提升机器学习算法的稳定性和准确性，它可以减少模型的方差从而避免overfitting。它通常应用在决策树方法中，其实它可以应用到任何其它机器学习算法中。如果大家对决策树的算法不太理解，请大家参考这篇文章：决策树ID3、C4.5、C5.0以及CART算法之间的比较，在下面的例子中，都会涉及到决策树，希望大家能理解一下这个算法。

下面，我介绍一下bagging技术的过程：

假设我有一个大小为$n$的训练集D，bagging会从D中有放回的均匀地抽样，假设我用bagging生成了$m个新的训练集D_i，每个D_i的大小为j$。由于我有放回的进行抽样，那么在$D_i$中的样本有可能是重复的。如果$j=n$，这种取样称为bootstrap取样。现在，我们可以用上面的$m$个训练集来拟合$m$个模型，然后结合这些模型进行预测。对于回归问题来说，我们平均这些模型的输出;对于分类问题来说，我们进行投票（voting）。bagging可以改良不稳定算法的性能，比如：人工神经网络、CART等等。下面，我举一个具体的例子说明一下bagging。

假设有一个训练集$D$的大小为7，我想用bagging生成3个新的训练集$D_i,每个D_i的大小为7$，结果如下表：

样本索引	$bagging（D_1）$	$bagging（D_2）$	$bagging（D_3）$
1	2	7	3
2	2	3	4
3	1	2	3
4	3	1	3
5	5	1	6
6	2	5	1
7	6	4	1

那么现在我就可以用上面生成的3个新训练集来拟合模型了。

决策树是一个很流行的机器学习算法。这个算法的性能在特征值的缩放和各种转换的情况下依然保持不变，即使在包含不相关特征的前提下，它依然很健壮。然而，决策树很容易过拟合训练集。它有低的偏差，但是有很高的方差，因此它的准确性不怎么好。

bagging是早期的集成方法（ensemble method），它可以重复地构建多个决策树基于有放回地重新采样，然后集成这些决策树模型进行投票，从而得到更好地准确性。稍后，我会介绍决策森林算法，它可以比bagging更好地解决决策树overfitting的问题。这些方法虽然会增加一些模型的偏差和丢失一些可解释性，但是它们通常会使模型具有更好地性能。

下面，我用scikit-learn实现bagging来拟合Wine数据集来实战一下bagging方法。这是数据集的介绍：Wine数据集

import pandas as pd
df_wine = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols', 'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue', 'OD280/OD315 of diluted wines', 'Proline']
df_wine = df_wine[df_wine['Class label'] != 1] # 数据集中有3个类别，这里我们只用其中的2个类别
y = df_wine['Class label'].values
X = df_wine[['Alcohol', 'Hue']].values # 为了可视化的目的，我们只选择2个特征

from sklearn.preprocessing import LabelEncoder
from sklearn.cross_validation import train_test_split
le = LabelEncoder()
y = le.fit_transform(y) # 把label转换为0和1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40,  random_state=1) # 拆分训练集的40%作为测试集

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
tree = DecisionTreeClassifier(criterion='entropy', max_depth=None)
# 生成500个决策树，详细的参数建议参考官方文档
bag = BaggingClassifier(base_estimator=tree, n_estimators=500, max_samples=1.0, max_features=1.0, bootstrap=True, bootstrap_features=False, n_jobs=1, random_state=1)

# 度量单个决策树的准确性
from sklearn.metrics import accuracy_score
tree = tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train, tree_test))
# Output：Decision tree train/test accuracies 1.000/0.854

# 度量bagging分类器的准确性
bag = bag.fit(X_train, y_train)
y_train_pred = bag.predict(X_train)
y_test_pred = bag.predict(X_test)
bag_train = accuracy_score(y_train, y_train_pred)
bag_test = accuracy_score(y_test, y_test_pred)
print('Bagging train/test accuracies %.3f/%.3f' % (bag_train, bag_test))
# Output：Bagging train/test accuracies 1.000/0.896

从上面的输出我们可以看出，Bagging分类器的效果的确要比单个决策树的效果好。下面，让我们打印出两个分类器的决策边界，看看它们之间有什么不同，代码如下：

x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
f, axarr = plt.subplots(nrows=1, ncols=2, sharex='col', sharey='row', figsize=(8, 3))

for idx, clf, tt in zip([0, 1], [tree, bag], ['Decision Tree', 'Bagging']):
    clf.fit(X_train, y_train)
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    axarr[idx].contourf(xx, yy, Z, alpha=0.3)
    axarr[idx].scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], c='blue', marker='^')
    axarr[idx].scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], c='red', marker='o')
    axarr[idx].set_title(tt)

plt.show()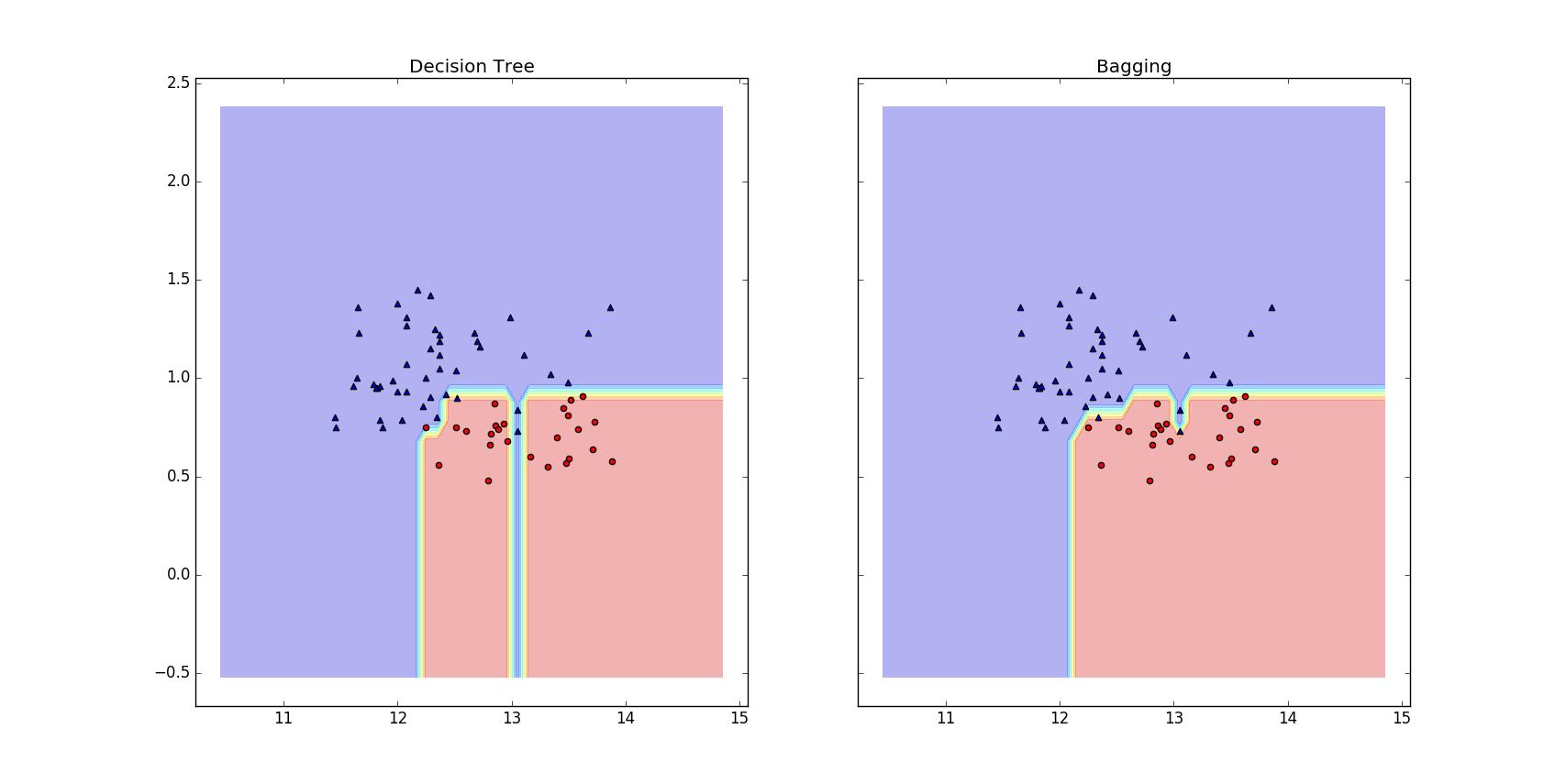

从上图我们可以看出，Bagging分类器的决策边界更加平滑。注意：bagging是不能减小模型的偏差的，因此我们要选择具有低偏差的分类器来集成，例如：没有修剪的决策树。

随机森林（random forests）

随机森林与上面Bagging方法的唯一的区别是，随机森林在生成决策树的时候用随机选择的特征。之所以这么做的原因是，如果训练集中的几个特征对输出的结果有很强的预测性，那么这些特征会被每个决策树所应用，这样会导致树之间具有相关性，这样并不会减小模型的方差。

随机森林通常可以总结为以下4个简单的步骤：

1. 从原始训练集中进行bootstrap抽样
2. 用步骤1中的bootstrap样本生成决策树
   
   • 随机选择特征子集
   • 用上面的特征子集来拆分树的节点
3. 重复1和2两个步骤
4. 集成所有生成的决策树进行预测

在上面的步骤2中，我们训练单个决策树的时候并没有用全部的特征，我们只用了特征的子集。假设我们全部的特征大小为$m$，那么$\\sqrt m$个特征子集是一个很好地选择。

随机森林并不像决策树一样有很好地解释性，这是它的一个缺点。但是，随机森林有更好地准确性，同时我们也并不需要修剪随机森林。对于随机森林来说，我们只需要选择一个参数，生成决策树的个数。通常情况下，你决策树的个数越多，性能越好，但是，你的计算开销同时也增大了。

下面，我用随机森林训练上面的Wine数据集。这次我不在只选择数据集的2个特征了，我要用全部的13个特征。而且这次的输出我用了3个类别。代码如下：

import pandas as pd
df_wine = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols', 'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue', 'OD280/OD315 of diluted wines', 'Proline']
y = df_wine['Class label'].values
X = df_wine.values[:, 1:]

from sklearn.preprocessing import LabelEncoder
from sklearn.cross_validation import train_test_split
le = LabelEncoder()
y = le.fit_transform(y) # 把label转换为0和1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40,  random_state=1) # 拆分训练集的40%作为测试集

from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=1000, criterion='gini', max_features='sqrt', max_depth=None, min_samples_split=2, bootstrap=True, n_jobs=1, random_state=1)
# 度量随机森林的准确性
rf = rf.fit(X_train, y_train)
y_train_pred = rf.predict(X_train)
y_test_pred = rf.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('Random Forest train/test accuracies %.3f/%.3f' % (tree_train, tree_test)) 

# output: Random Forest train/test accuracies 1.000/0.986

对于上面RandomForestClassifier类的参数信息，我强烈建议大家去官网查看：RandomForestClassifier类

Boosting

声明：下面的部分内容是我从Bishop模式识别与机器学习（Pattern Recognition and Machine Learning）书中翻译下来的，如果你想对Boosting有一个更深刻的理解，我建议你读书中的14.3节。

Boosting集合多个’base’分类器从而使它的性能比任何单个base分类器都好地多。在这个小节中，我描述一个更广泛使用的boosting算法adaptive boosting（AdaBoost）。即使base分类器的性能比随机猜测稍微好一点（因此base分类器也叫做weak learners），Boosting依旧会得到一个很好地预测结果。Boosting最初的目的是解决分类问题，现在它也可以解决回归问题。

Boosting与Bagging主要的不同是：Boosting的base分类器是按顺序训练的（in sequence），训练每个base分类器时所使用的训练集是加权重的，而训练集中的每个样本的权重系数取决于前一个base分类器的性能。如果前一个base分类器错误分类地样本点，那么这个样本点在下一个base分类器训练时会有一个更大的权重。一旦训练完所有的base分类器，我们组合所有的分类器给出最终的预测结果。过程如下图：

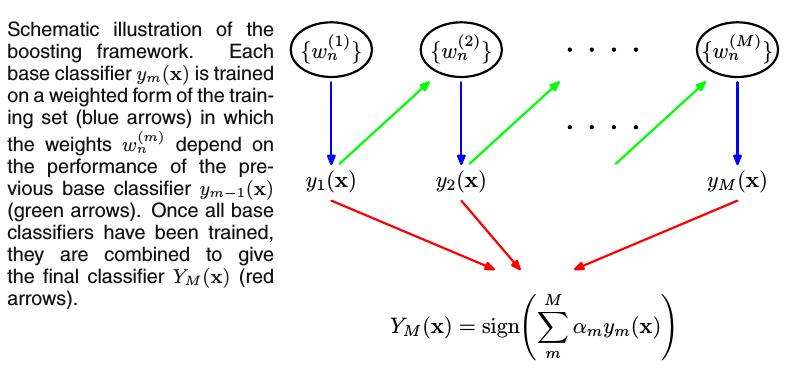
上图中，每个base分类器$y_m(x)$用加权重的训练集来训练（蓝色箭头）， 训练集的权重系数$w_n^{(m)}$取决于上个base分类器$y_{m-1}(x)$(绿色箭头)的性能。一旦所有的base分类器训练完成，结合它们给出最终的分类器$Y_M(x)$(红色箭头)。

下面，给出一个两类别的分类问题。输入向量$x_1, x_2, \\dots, x_N$构成了训练集样本，其对应的目标变量（标签）为$t_1, t_2, \\dots, t_N$，其中$t_n \\in \\{-1, 1\\}$。每个训练样本给一个初始化权重$\\frac{1}{N}$.假设我们有一个现成的程序（ 关于Bagging

分类器组合方法Bootstrap, Boosting, Bagging, 随机森林

快速理解bootstrap,bagging,boosting，gradient boost-三个概念

Bagging与Boosting的联系与区别

改进bagging，成为Boosting！

SIGAI机器学习第十九集 随机森林