2014年 蓝桥杯决赛(Java)
Posted piaocoder
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2014年 蓝桥杯决赛(Java)相关的知识,希望对你有一定的参考价值。
国王的遗产
X国是个小国。国王K有6个儿子。在临终前,K国王立下遗嘱:国王的一批牛作为遗产要分给他的6个儿子。
其中,大儿子分1/4,二儿子1/5,三儿子1/6,....
直到小儿子分1/9。
牛是活的,不能把一头牛切开分。
最后还剩下11头牛,分给管家。
请计算国王这批遗产中一共有多少头牛。
这是一个整数,请通过浏览器提交答案,不要填写任何多余的内容(比如说明性的文字)
2520
public class Main{
public static void main(String[] args) {
int sum = 4*5*6*7*8*9;
int x = sum/4+sum/5+sum/6+sum/7+sum/8+sum/9;
System.out.println(11*sum/(sum-x));
}
}
六角幻方(搜索)
把 1 2 3 ... 19 共19个整数排列成六角形状,如下:
* * *
* * * *
* * * * *
* * * *
* * *
要求每个直线上的数字之和必须相等。共有15条直线哦!
再给点线索吧!我们预先填好了2个数字,第一行的头两个数字是:15 13,参见下图,黄色一行为所求。
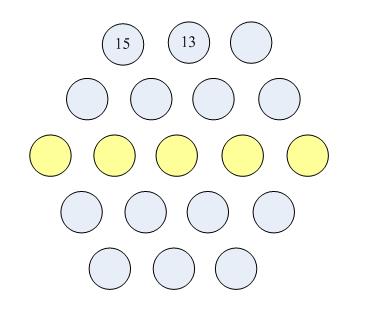
请你填写出中间一行的5个数字。数字间用空格分开。
这是一行用空格分开的整数,请通过浏览器提交答案,不要填写任何多余的内容(比如说明性的文字等)
9 6 5 2 16
public class Main{
static int[] table = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19};
public static void main(String[] args){
int arr[] = new int[16];
boolean[] vis = new boolean[20];
vis[15] = vis[13] = vis[10] = true;
dfs(arr,0,vis);
}
static void dfs(int[] arr,int step, boolean[] vis){
if(step == 4){
if(arr[0]+arr[1]+arr[2]+arr[3] != 38)
return ;
}else if(step == 5){
if(15+arr[0]+arr[4] != 38)
return ;
}else if(step == 9){
if(arr[4]+arr[5]+arr[6]+arr[7]+arr[8] != 38 ||
10+arr[3]+arr[8] != 38)
return ;
}else if(step == 10){
if(13+arr[1]+arr[5]+arr[9] != 38)
return ;
}else if(step == 13){
if(arr[9]+arr[10]+arr[11]+arr[12] != 38 ||
13+arr[2]+arr[7]+arr[12] != 38)
return ;
}else if(step == 14){
if(10+arr[2]+arr[6]+arr[10]+arr[13] != 38 ||
arr[4]+arr[9]+arr[13] != 38)
return ;
}
else if(step == 15){
if(arr[0]+arr[5]+arr[10]+arr[14] != 38 ||
arr[3]+arr[7]+arr[11]+arr[14] != 38)
return ;
}
else if(step == 16){
if(arr[13]+arr[14]+arr[15] != 38 ||
15+arr[1]+arr[6]+arr[11]+arr[15] != 38 ||
arr[8]+arr[12]+arr[15] != 38)
return ;
print(arr);
}
for(int i = 0; i < table.length; ++i){
if(vis[table[i]] == false){
vis[table[i]] = true;
arr[step] = table[i];
dfs(arr,step+1,vis);
vis[table[i]] = false;
}
}
}
static void print(int[] arr){
for(int i = 0; i < arr.length; ++i){
System.out.print(arr[i]+" ");
}
System.out.println();
}
}
格子放鸡蛋
X星球的母鸡很聪明。它们把蛋直接下在一个 N * N 的格子中,每个格子只能容纳一枚鸡蛋。它们有个习惯,要求:每行,每列,以及每个斜线上都不能有超过2个鸡蛋。如果要满足这些要求,母鸡最多能下多少蛋呢,有多少种摆放方法呢?
下面的程序解决了这个问题,请仔细分析程序逻辑,推断划线处缺少的代码。
public class A
{
static int max = 0;
static int T = 0;
static final int N = 6;
// 只能在(r,c) 以及其右,其下放置
static void f(int[][] da, int r, int c)
{
if(r>=N){
int n = count(da);
if(n>max) {
max= n;
T= 0;
}
if(n==max) T++;
return;
}
//计算一下步放哪
int r_next = r;
int c_next = c +1;
if(c_next>=N){
c_next = 0;
r_next++;
}
if(____________________){ // 填空位置
da[r][c] = 1;
f(da, r_next, c_next);
}
da[r][c] = 0;
f(da, r_next,c_next);
}
static int count(int[][] da)
{
int n = 0;
for(int i=0;i<da.length; i++)
for(int j=0;j<da[i].length; j++)
if(da[i][j]==1) n++;
return n;
}
static int spy(int[][] da, int r, int c)
{
int m=0;
// 该行
int n=0;
for(int i=0;i<N; i++) if(da[r][i]==1) n++;
if(n>m) m = n;
//该列
n=0;
for(int i=0;i<N; i++) if(da[i][c]==1) n++;
if(n>m) m = n;
//右斜线
n=0;
for(int i=0;i<N; i++){
if(r-i<0 || c-i<0) break;
if(da[r-i][c-i]==1) n++;
}
for(int i=1;i<N; i++){
if(r+i>=N || c+i>=N) break;
if(da[r+i][c+i]==1) n++;
}
if(n>m) m = n;
//左斜线
n=0;
for(int i=0;i<N; i++){
if(r-i<0 || c+i>=N) break;
if(da[r-i][c+i]==1) n++;
}
for(int i=1;i<N; i++){
if(r+i>=N || c-i<0) break;
if(da[r+i][c-i]==1) n++;
}
if(n > m) m =n;
return m;
}
public static void main(String[] args)
{
int[][] da = newint[N][N];
f(da, 0, 0);
System.out.println(max);
System.out.println(T);
}
}
注意:通过浏览器提交答案。只填写缺少的内容,不要填写任何多余的内容(例如:说明性文字或已有符号)。
spy(da,r,c) <= 2
排列序数
如果用a b c d这4个字母组成一个串,有4!=24种,如果把它们排个序,每个串都对应一个序号:
abcd 0
abdc 1
acbd 2
acdb 3
adbc 4
adcb 5
bacd 6
badc 7
bcad 8
bcda 9
bdac 10
bdca 11
cabd 12
cadb 13
cbad 14
cbda 15
cdab 16
cdba 17
...
现在有不多于10个两两不同的小写字母,给出它们组成的串,你能求出该串在所有排列中的序号吗?
【输入格式】
一行,一个串。
【输出格式】
一行,一个整数,表示该串在其字母所有排列生成的串中的序号。注意:最小的序号是0。
例如:
输入:
bdca
程序应该输出:
11
再例如:
输入:
cedab
程序应该输出:
70
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
import java.util.Arrays;
import java.util.Scanner;
public class Main{
static String str;
static char[] arr,target;
static int count;
public static void main(String[] args){
Scanner sca = new Scanner(System.in);
str = sca.nextLine();
arr = str.toCharArray();
Arrays.sort(arr);
boolean[] vis = new boolean[20];
target = new char[arr.length];
dfs(0,vis);
}
private static void dfs(int step, boolean[] vis) {
// TODO Auto-generated method stub
if(step == target.length){
if(str.equals(String.valueOf(target))){
System.out.println(count);
}
++count;
return ;
}
for(int i = 0; i < target.length; ++i){
if(!vis[i]){
vis[i] = true;
target[step] = arr[i];
dfs(step+1,vis);
vis[i] = false;
}
}
}
}
幂一矩阵
天才少年的邻居 atm 最近学习了线性代数相关的理论,他对“矩阵”这个概念特别感兴趣。矩阵中有个概念叫做幂零矩阵。对于一个方阵 M ,如果存在一个正整数 k 满足 M^k = 0 ,那么 M 就是一个幂零矩阵。(^ 表示乘方)
atm 不满足幂零矩阵,他自己设想了一个幂一矩阵:对于一个方阵 M ,如果存在一个正整数 k 满足 M^k = I ,其中 I 是单位矩阵,那么 M 就是一个幂一矩阵。
atm 特别钟情于这样一种方阵:每行每列有且仅有一个 1 。经过 atm 不断实验,他发现这种矩阵都是幂一矩阵。
现在,他的问题是,给定一个满足以上条件的方阵,他想求最小的 k 是多少。
【输入格式】
第一行一个正整数 n ,表示矩阵大小是 n * n。
接下来 n 行,每行两个正整数 i j 表示方阵的第 i 行第 j 列为 1。
1 <= i, j <= n 。
行号,列号都从1开始。
【输出格式】
一行。一个正整数,即题目中所说最小的 k 。
【样例输入】
5
3 1
1 2
4 4
2 3
5 5
【样例输出】
3
【数据范围】
对于 30% 的数据满足 n <=10
对于 60% 的数据答案不超过 10^18
对于 100% 的数据满足 n <=10000
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
解题思路:
首先求出每一行的1的位置经过多少次会等于它的行数,然后求出这些值的最小公倍数即可。
import java.math.BigInteger;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sca = new Scanner(System.in);
int n = sca.nextInt();
int[] row = new int[n + 1];
int[] pos = new int [n + 1];
int count [] = new int [n + 1];
HashSet<Integer> hashset = new HashSet<Integer>();
for(int i = 0; i < n; ++i){
int x = sca.nextInt();
int y = sca.nextInt();
pos[x] = y;
row[x] = y;
}
for(int i = 1; i <= n; ++i) {
hashset.add(cal(row, pos, i));
}
Iterator<Integer> iter = hashset.iterator();
BigInteger sum = new BigInteger(iter.next()+"");
while(iter.hasNext()){
BigInteger next = new BigInteger(iter.next()+"");
BigInteger gcd = GCD(sum,next);
sum = sum.divide(gcd).multiply(next);
}
System.out.println(sum);
}
private static BigInteger GCD(BigInteger sum, BigInteger next) {
// TODO Auto-generated method stub
if(next.equals(BigInteger.ZERO))
return sum;
else
return GCD(next,sum.mod(next));
}
private static int cal(int[] row, int[] pos, int i) {
// TODO Auto-generated method stub
int tmp = 1;
while(true){
row[i] = pos[row[i]];
tmp++;
if(row[i] == i)
break;
}
if(tmp == 2)
return 1;
return tmp;
}
}
供水设施
X星球的居民点很多。Pear决定修建一个浩大的水利工程,以解决他管辖的N个居民点的供水问题。现在一共有N个水塔,同时也有N个居民点,居民点在北侧从1号到N号自西向东排成一排;水塔在南侧也从1号到N号自西向东排成一排。
N条单向输水线(有水泵动力),将水从南侧的水塔引到北侧对应的居民点。
我们不妨将居民点和水塔都看做平面上的点,居民点坐标为(1,K)~(N,K),水塔为(1,0)~(N,0)。
除了N条纵向输水线以外,还有M条单向的横向输水线,连接(Xi,Yi)和(Xi,(Yi)+1)或者(Xi,Yi)和(Xi,(Yi)-1)。前者被称为向右的水路,而后者是向左的。不会有两条水路重叠,即便它们方向不同。
布局的示意图如:

显然,每个水塔的水都可以到达若干个居民点(而不仅仅是对应的那个)。例如上图中,4号水塔可以到达3、4、5、6四个居民点。
现在Pear决定在此基础上,再修建一条横向单项输水线。为了方便考虑,Pear认为这条水路应当是自左向右的,也就是连接了一个点和它右侧的点(例如上图中连接5和6两个纵线的横向水路)。
Pear的目标是,修建了这条水路之后,能有尽可能多对水塔和居民点之间能到达。换句话说,设修建之后第i个水塔能到达Ai个点,你要最大化A1+A2+...+An。
根据定义,这条路必须和X轴平行,但Y坐标不一定要是整数。注意:虽然输入中没有重叠的水路,但是你的方案可以将新修的输水线路与已有的水路重叠。
【输入数据】
输入第一行包含三个正整数N,M,K,含义如题面所述:N是纵向线数,M横向线数,K是居民点纵坐标。
接下来M行,每行三个整数。前两个正整数Xi Yi表示水路的起点坐标;
1<=Xi<=N,0<Yi<K。
接下来一个数0或者1,如果是0表示这条水路向左,否则向右。
保证水路都是合法的,也就是不会流向没有定义的地方。
【输出数据】
输出一行。是一个正整数,即:题目中要求的最大化的A1+A2+...+An。
【输入样例1】
4 3 2
1 1 1
3 1 0
3 1 1
【输出样例1】
11
【输入样例2】
7 9 4
2 3 0
7 2 0
6 3 1
6 1 0
2 1 1
3 3 1
5 2 0
2 2 1
7 1 0
【输出样例2】
21
【数据范围】
对于20%的数据,N,K<=20,M<=100
对于40%的数据,N,K<=100,M<=1000
对于60%的数据,N,K<=1000,M<=100000
对于100%的数据,N,K<=50000,M<=100000
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 5000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
官方题解:
首先不难发现:修建水渠的肯定是 y 坐标整点。因此对于 20%的数据,暴力枚举哪一 个位置修建水渠即可。接下来我们需要观察
出,这是一个平面图,因而每个点能到达的居 民点一定是连续的一段(因为有南北向水渠所以这一点比较显然)。接下来,如果把
N 个水塔能到达的居民点区间都求出来,则区间是单调不降的。这同样取决于平面图的性质。 由于没有(双向)重边,所以图肯定
是一个拓扑图。要想得到每个水塔能到达哪些居 民点,只要把拓扑图构出来,并按拓扑序进行 dp(得到每个点能到达的最左最右
点即可)。 接下来枚举那条添加的边。这条边肯定是加在某个“关键点”向右的——所谓关键点就是 所有居民点、路的端点、水塔。
枚举它一共有 O(M+N)种情况。这条路必然把原来的一个点 向右的距离扩展了一段。接下来,假设这个点能由[l,r]这一段居民点到达
(这里易知也 是连续的,可以在反图上 dp 求出),那么就相当于这些区间的右端点都和某个数取 max。 因为右端点有序,所以很
容易维护。其它之前提到的操作都可以用 stl 解决。 整个算法复杂度为 O(NlogN)。用 O(N^2)等较劣的算法直接实现可得 60 分或
40 分。
以上是关于2014年 蓝桥杯决赛(Java)的主要内容,如果未能解决你的问题,请参考以下文章