MT200一道自招的不等式

Posted 2020-11-19 青春的记忆

(2018武汉大学自招)设$x,y,z\\ge0,xy+yz+zx=1$证明:$\\dfrac{1}{x+y}+\\dfrac{1}{y+z}+\\dfrac{1}{z+x}\\ge \\dfrac{5}{2}$

(2018武汉大学自招)设$x,y,z\\ge0,xy+yz+zx=1$证明:$\\dfrac{1}{x+y}+\\dfrac{1}{y+z}+\\dfrac{1}{z+x}\\ge \\dfrac{5}{2}$

证明:
\\begin{align*}
\\textbf{原式} & \\iff 2\\sum{(y+z)(z+x)}-5\\prod(x+y)\\ge0\\\\
& \\iff 2\\sum{z^2+(x+y)z+xy}-5\\left((x+y+z)(xy+yz+zx)-xyz\\right)\\ge0\\\\
& \\iff 2(x+y+z)^2+2-5(x+y+z)+5xyz\\ge0
\\end{align*}
记$a=x+y+z,b=xy+yz+zx,c=xyz$则只需证明:$2a^2-5a+5c+2\\ge0$
若$a>2$则$2a^2-5a+5c+2\\ge2a^2-5a+2=(2a-1)(a-2)\\ge0$成立
若$a\\le2$则由舒尔不等式:
$\\sum{x(x-y)(x-z)=(\\sum x)^3-4\\sum{x}\\sum{xy}+9xyz=a^3-4ab+9c=a^3-4a+9c\\ge0}$ 得
$c\\ge\\dfrac{-a^3+4a}{9}$
故$2a^2-5a+5c+2\\ge\\dfrac{-5a^3+18a^2-25a+18}{9}\\ge0$(由单调递减易得)当$(x,y,z)=(1,1,0)$时取到等号.

事实上还有如下天书上的证明:

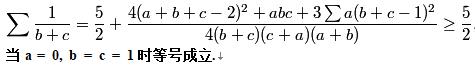（Chen  Ji )

事实上还可证明最大值:
$x,y,z\\ge0,xy+yz+zx=1$时$\\dfrac{1}{x+y}+\\dfrac{1}{y+z}+\\dfrac{1}{z+x}\\le\\sqrt{\\dfrac{27}{4}}$
提示:利用均值:$\\dfrac{1}{x+y}+\\dfrac{1}{y+z}+\\dfrac{1}{z+x}\\le\\sqrt{3\\sum\\dfrac{1}{(x+y)^2}}\\le\\sqrt{\\dfrac{27}{4}}$
最后一步是著名的伊朗96不等式.
最后给一个利用上面方法的练习:(2011年全国联赛B卷二试第三题）

已知$a,b,c\\ge1$且满足:$abc+2a^2+2b^2+2c^2+ca-cb-4a+4b-c=28,$求$a+b+c$的最大值.