一道非常综合的好题然后就莫名其妙地知道了动态LCA的求法
果然是ZJOI的题目,只能说这思路服了
首先我们发现每次操作只会灭绝一种动物,然后我们想一下就知道如果有\\(n(n>=2)\\)个食物的动物就不会灭绝。
然后我们YY一个叫灭绝树的东西,在这个树上的点都满足一个性质:当一个节点被割去时,以它为根的整棵子树对应的动物都会灭亡。
然后我们只需要考虑如何搞出这个树了。
然后我们再YY一个虚拟节点0,让它向所有生产者连边,我们可以形象得理解成太阳。
然后我们将题目中的树反向建边,然后就变成了这样:
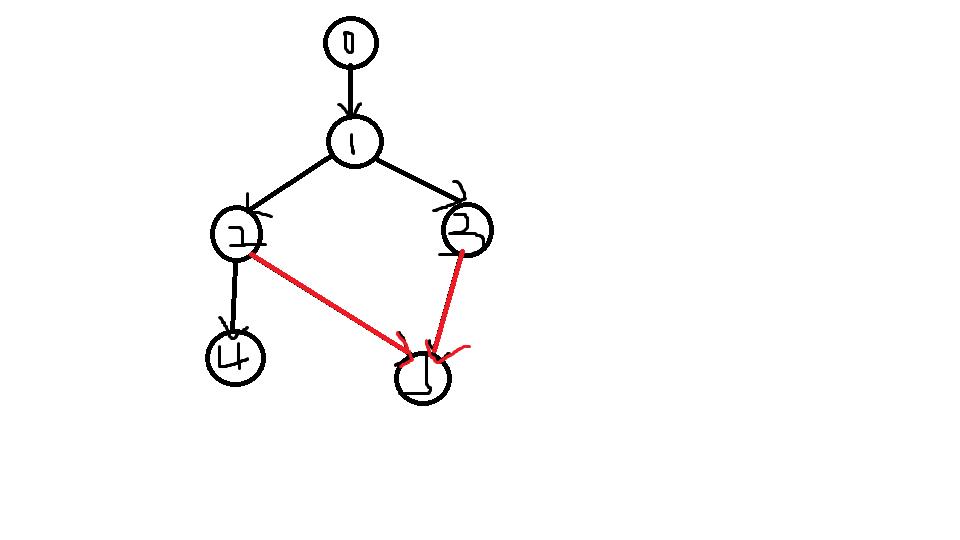
然后我们发现5号点很难受,因为有两个点连向它。那么如果只割一个点怎么让5号点灭绝。
答案很简单:只需要让它的两个父节点都灭绝即可
然后我们看要让2,3号点都灭绝,那么:
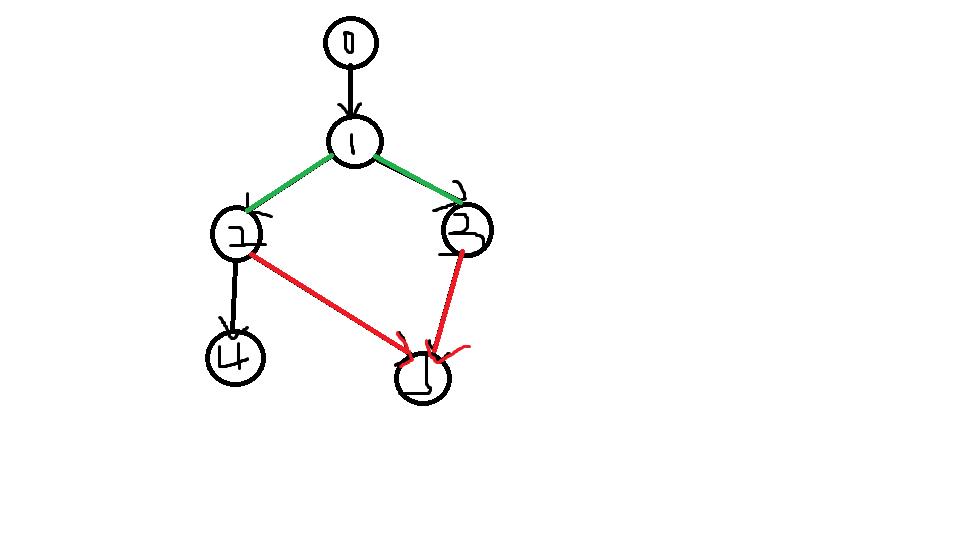
只需要让1灭绝即可。那么1与2,3的关系就很简单了:1是2,3的LCA
那么就很好办了,我们只需要按顺序找出每一个点的所有父节点的LCA,然后在灭绝树上把这个点挂在它的LCA下面即可。
但是这个顺序怎么办,我们注意到题目中提到了:
这个图没有环。
然后就我们从0开始拓扑排序即可确定这个顺序,然后就只求LCA了
这里注意因为我们没有刚开始就把图建出来,所以DFS序+RMQ和Tarjan的方法就不能用了。
所以我们用倍增,每次将一个点挂上树时然后单独更新它的LCA信息
然后就可以解决了,不得不吐槽一下这道题开了三个邻接表,还是很狗的,因为这个调了很久
CODE
#include<cstdio>
#include<cstring>
using namespace std;
const int N=70000,P=20;
struct edge
{
int to,next;
}e[N<<2],re[N<<2],new_e[N<<1];
int head[N],rhead[N],new_head[N],dep[N],ru[N],q[N],father[N][P],size[N],tot,sum,cnt,rcnt,new_cnt,n,x,rt;
inline char tc(void)
{
static char fl[100000],*A=fl,*B=fl;
return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
x=0; char ch=tc();
while (ch<\'0\'||ch>\'9\') ch=tc();
while (ch>=\'0\'&&ch<=\'9\') x=x*10+ch-\'0\',ch=tc();
}
inline void write(int x)
{
if (x/10) write(x/10);
putchar(x%10+\'0\');
}
inline void add(int x,int y)
{
e[++cnt].to=y; e[cnt].next=head[x]; head[x]=cnt;
}
inline void radd(int x,int y)
{
re[++rcnt].to=y; re[rcnt].next=rhead[x]; rhead[x]=rcnt;
}
inline void new_add(int x,int y)
{
new_e[++new_cnt].to=y; new_e[new_cnt].next=new_head[x]; new_head[x]=new_cnt;
}
inline void swap(int &a,int &b)
{
int t=a; a=b; b=t;
}
inline void top_sort(void)
{
register int i; int H=0,T=0;
for (i=1;i<=n;++i)
if (!ru[i]) q[++T]=i,father[i][0]=rt,dep[i]=1,new_add(rt,i),new_add(i,rt);
while (H<T)
{
int now=q[++H];
for (i=head[now];i!=-1;i=e[i].next)
if (!(--ru[e[i].to])) q[++T]=e[i].to;
}
}
inline void rebuild(int now)
{
for (register int i=0;i<P-1;++i)
if (father[now][i]^-1) father[now][i+1]=father[father[now][i]][i];
}
inline int LCA(int x,int y)
{
register int i;
if (dep[x]<dep[y]) swap(x,y);
for (i=P-1;i>=0;--i)
if (father[x][i]^-1&&dep[father[x][i]]>=dep[y]) x=father[x][i];
if (!(x^y)) return x;
for (i=P-1;i>=0;--i)
if (father[x][i]^-1&&father[y][i]^-1&&father[x][i]^father[y][i]) x=father[x][i],y=father[y][i];
return father[x][0];
}
inline void get_tree(void)
{
register int i,j;
for (i=1;i<=n;++i)
{
int now=q[i];
if (!(father[now][0]^-1))
{
int fa=-1;
for (j=rhead[now];j!=-1;j=re[j].next)
if (fa^-1) fa=LCA(fa,re[j].to); else fa=re[j].to;
if (!(fa^-1)) fa=0;
father[now][0]=fa; new_add(fa,now); new_add(now,fa); dep[now]=dep[fa]+1; rebuild(now);
}
}
}
inline void DFS(int now,int fa)
{
size[now]=1;
for (register int i=new_head[now];i!=-1;i=new_e[i].next)
if (new_e[i].to^fa) DFS(new_e[i].to,now),size[now]+=size[new_e[i].to];
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
register int i; read(n); memset(father,-1,sizeof(father));
memset(e,-1,sizeof(e)); memset(head,-1,sizeof(head));
memset(re,-1,sizeof(re)); memset(rhead,-1,sizeof(rhead));
memset(new_e,-1,sizeof(new_e)); memset(new_head,-1,sizeof(new_head));
for (i=1;i<=n;++i)
for (read(x);x;read(x))
add(x,i),radd(i,x),++ru[i];
top_sort(); get_tree(); DFS(rt,-1);
for (i=1;i<=n;++i)
write(size[i]-1),putchar(\'\\n\');
return 0;
}