Undirected Graphs

Posted 2020-11-11 archeroc

无向图

Introduction

图是由边连接的点的集合，有着广泛的应用空间。

一些图的术语，点，边，路径，环（圈），连通分量（子图）。

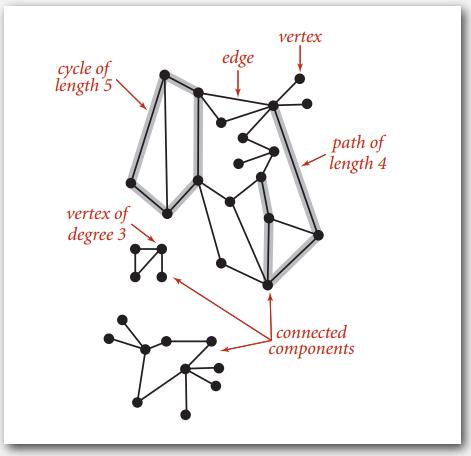
简单路径不重复经过点，简单环不含有重复点和边，简单图不含自环和平行边。

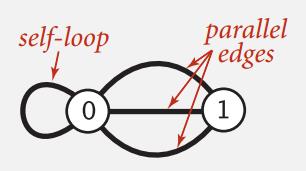
树是一幅无环连通图。互不相连的树组成的集合称为森林。连通图的生成树是它的一幅子图，它含有图中的所有顶点且是一棵树。图的生成树森林是它的所有连通子图的生成树的集合。当且仅当一幅含有 V 个结点的图 G 满足下列 5 个条件之一时，它是一棵树：

• G 有 V-1 条边且不含有环
• G 有 V-1 条边且是连通的
• G 是连通的，但删除任意一条边都会使它不再连通
• G 是无环图，但添加任意一条边都会产生一条环
• G 中的任意一对顶点之间仅存在一条简单路径

Graph-API

对于有 V 个节点的图，我们使用整数 0 到 V-1 来简化表示，反正可以用符号表把实际名称和数字对应起来。惯例先给出 API 和示例程序，然后再谈具体实现。

API

Sample Client

运行示例

在这些简单的基础操作之上，我们才能实现一些常用的图处理代码，像是计算 v 的度（有几条边），图的最大度等等，现在的问题是用哪种方式（数据结构）来表示图并实现这份 API。

Set-of-edges

维护一个包含图中所有边的集合，用数组或是链表实现。但是，这样的话实现 adj() （查询某个节点的所有边）需要检查图中所有的边，显然太慢了。

Adjacency-matrix

邻接矩阵。维护一个 v 乘 v 的布尔矩阵 adj[][]，若节点 v 和节点 w 之间有条边，则 adj[v][w] 和 adj[w][v] 为 true 。但是，这样的话，显然当 v 很大的时候会需要很大的内存，也是不合适的，而且邻接矩阵也不支持平行边。

Adjacency-list

邻接表。维护一个链表的数组，每个链表对应一个节点所有与它相连的点。

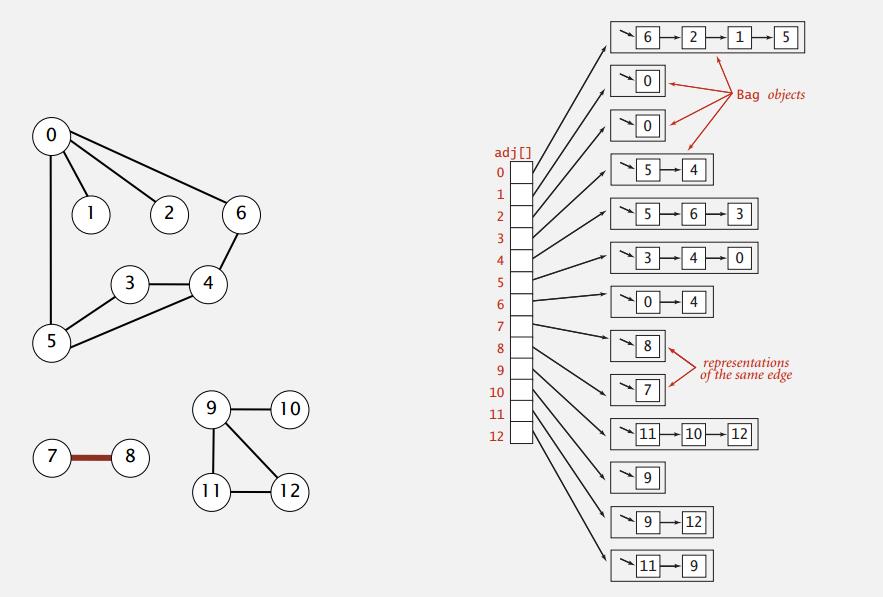
在实际中，我们使用邻接表来表示图，因为算法基于迭代点的相邻点，且真实世界中的往往是稀疏图（点相对边来说多得多）。邻接表需要的内存正比于 E+V，添加边需要的时间是常数，判断两点间是否有边的时间和点的度成正比，遍历点的所有相邻点的时间和点的度成正比，对这些操作来说已经是最优的了。

Java Implementation

public class Graph {
    private final int V;
    private Bag<Integer>[] adj;    //adjacency lists(using Bag data type)

    public Graph(int V) {
        this.V = V;
        // create empty graph with V vertices
        adj = (Bag<Integer>[]) new Bag[V];
        for (int v = 0; v < V; v++)
            adj[v] = new Bag<Integer>();
    }

    // add edge v-w(parallel edges and self-loops allowed)
    public void addEdge(int v, int w) {
        adj[v].add(w);
        adj[w].add(v);
    }

    // iterator for vertices adjacent to v
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

Depth First Search

我们常常通过系统地检查每一个顶点和每一条边来获取图的各种性质。

Maze Exploration

与图搜索类似的走迷宫有种古老的 Tremaux 方法。

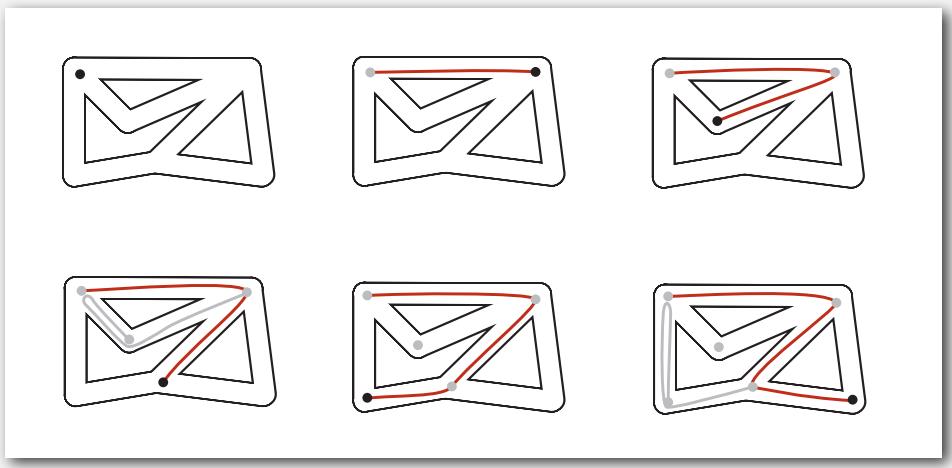
用绳子标记你走过的路，没路走的时候就沿着绳子返回找其它路，直到找到出路。

深度优先搜索是同样的原理，一条路走到底，没路就返回找其它路，按这样的策略系统地遍历整个图。典型的应用是对于一个给定的点找到所有和它相连的点，以及找出两个点之间的路径。

Design Pattern

因为我们会讨论大量关于图处理的算法，所以对于图的处理算法的设计模式，首要目标是将图的表示和实现分离开来。为此，我们会为每个任务创建一个相应的类，用例可以创建相应的对象来完成任务。典型的用例程序会构造一幅图，将图传递给实现了某个算法的类（作为构造函数的参数）。

对于上面典型应用，我们这样设计。

DFS

• boolean[] marked 判断点是否访问过
• int[] edgeTo 保存访问点的源，用来还原路径

// recursive DFS
private void dfs(Graph G, int v) {
    marked[v] = true;
    for (int w : G.adj(v)) {
        if (!marked[w]) {
            dfs(G, w);
            edgeTo[w] = v;
        }
    }
}

DFS 之后，所有与给定点 s 相连的点都会被标记为访问过。

Implementation

public boolean hasPathTo(int v) {
    return marked[v];
}

public Iterable<Integer> pathTo(int v) {
    if (!hasPathTo(v)) {
        return null;
    }

    Stack<Integer> path = new Stack<Integer>();
    for (int x = v; x != s; x = edgeTo[x]) {
        path.push(x);
    }
    path.push(s);
    return path;
}

在 DFS 之后，能在常数时间判断点是否与给定的点相连，找到这条相连路径需要的时间正比与路径的长度。

Breadth First Search

广度优先搜索采用不同的策略来遍历图中的点。

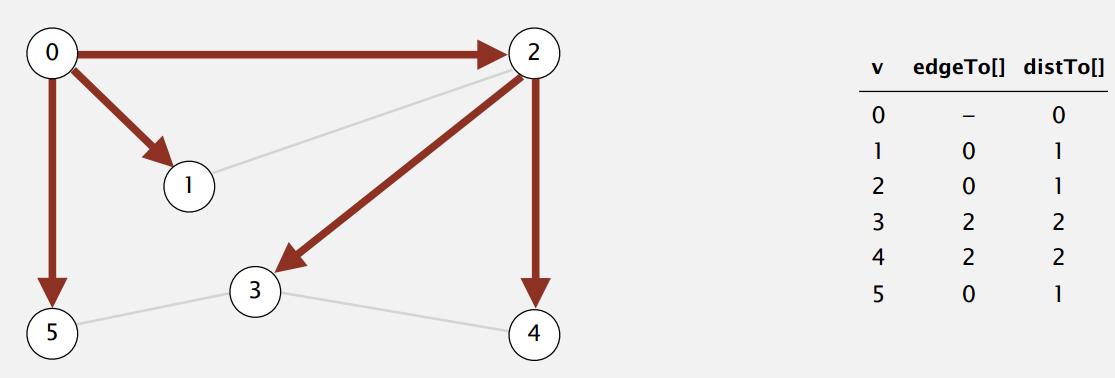
BFS 把没访问过的点放在队列（Queue）里存起来，然后按先进先出的顺序继续拓展搜索。像上图，从 0 开始搜索，把没访问过的 2 、 1 、 5 先后放入队列，然后下次就是拓展 2 这个点。从图上来看就是按源一层一层地搜索，搜完距离为 1 的再搜距离为 2 的，所以 BFS 找到的两点间路径是最短的。

其实 DFS 相当于把没访问过的点存在栈（Stack）里，然后按先进后出的顺序把这些点拿出来继续拓展搜索，从图上来看就是会一条路走到底，再返回找就近的其它路。上面 DFS 实现没有显式地使用 Stack 这个数据结构，其实是隐含在函数递归调用的函数栈里了。

BFS

private void bfs(Graph G, int s) {
    Queue<Integer> q = new Queue<Integer>();
    q.enqueue(s);
    marked[s] = true;
    while (!q.isEmpty()) {
        int v = q.dequeue();
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                q.enqueue(w);
                marked[w] = true;
                edgeTo[w] = v;
            }
        }
    }
}

BFS 按点到源点的距离从近到远遍历图，需要的时间和 E+V 成正比，之后的实现和上面一样。

Connected Components

连通分量，和 Union Find 中讨论的一样，满足：

1. symmetric: 自反性， p 和 p 自身是连通的。
2. transitive: 传递性，如果 p 和 q 连通，又有 q 和 r 连通，那么 p 和 r 连通。
3. reflexive: 对称性， p 和 q 连通，则 q 和 p 连通。

DFS 的下一个直接应用就是找出一幅图的所有连通分量。

连通分量 API

Implementation With DFS

public class CC {
    private boolean[] marked;
    private int[] id;    // id[v] = id of component containing v
    private int count;   // number of components

    public CC(Graph G) {
        marked = new boolean[G.V()];
        id = new int[G.V()];

        // run DFS from one vertex in each component
        for (int v = 0; v < G.V(); v++) {
            if (!marked[v]) {
                dfs(G, v);
                count++;
            }
        }
    }

    public int count() {
        return count;
    }

    public int id(int v) {
        return id[v];
    }

    private void dfs(Graph G, int v) {
        marked[v] = true;

        // all vertices discovered in
        // same call of dfs hava same id
        id[v] = count;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
    }
}

DFS 预处理图之后，能在常数时间内判断 v 和 w 是否连通。

相比之下 union-find 算法是一种动态算法，不像 DFS 需要对图进行预处理。我们在完成只需要判断连通性或是需要完成有大量连通性查询和插入操作混合等类似的任务时，更倾向使用 union-find 算法，而 DFS 则更适合实现图的抽象数据类型，因为它能够更有效地利用已有的数据结构。

Challenges

介绍了一些图处理的问题，这里不做展开，稍微提些。

• 双色问题（bipartite）。能够用两种颜色给点着色，使每条边的两个端点颜色都不一样吗（二分图）？

• 欧拉环（Eulerian tour）。找到一个包含且仅包含一次所有边的环。

• 汉密尔顿环（Hamiltonian tour）。找到一个经过且只经过一次所有点的环。

booksite-4.1 上 “DFS 的更多应用” 部分给出了解决的代码，感兴趣可以自己去看，另外上面其它示例的完整代码也都有。