hdu 1730 Nim博弈

Posted 2020-11-09 starry

Tom和Jerry正在玩一种Northcott游戏，可是Tom老是输，因此他怀疑这个游戏是不是有某种必胜策略，郁闷的Tom现在向你求救了，你能帮帮他么？ 
游戏规则是这样的： 
　　如图所示，游戏在一个n行m列（1 ≤ n ≤ 1000且2 ≤ m ≤ 100）的棋盘上进行，每行有一个黑子（黑方）和一个白子（白方）。执黑的一方先行，每次玩家可以移动己方的任何一枚棋子到同一行的任何一个空格上，当然这过程中不许越过该行的敌方棋子。双方轮流移动，直到某一方无法行动为止，移动最后一步的玩家获胜。Tom总是先下（黑方）。图1是某个初始局面，图二是Tom移动一个棋子后的局面（第一行的黑子左移两步）。 

 

图1

 

图2

Input　　输入数据有多组。每组数据第一行为两个整数n和m，由空格分开。接下来有n行，每行两个数Ti，Ji (1 ≤ Ti, Ji ≤ m)分别表示Tom和Jerry在该行棋子所处的列数。 
　　 注意：各组测试数据之间有不定数量的空行。你必须处理到文件末。 
Output对于每组测试数据输出一行你的结果。如果当前局面下Tom有必胜策略则输出“I WIN!”，否则输出“BAD LUCK!”。Sample Input

3 6
4 5
1 2
1 2

3 6
4 5
1 3
1 2

Sample Output

BAD LUCK!
I WIN!

 

类似与Nim博弈，取决于相邻之间的格子。如果是零 一定是先手输的。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int main() {
 5     int n, m;
 6     while(scanf("%d%d", &n, &m)!= EOF) {
 7         int ans = 0, a, b;
 8         while(n--) {
 9             cin >> a >> b;
10             ans ^= abs(a-b)-1;
11         }
12         if(ans) printf("I WIN!\n");
13         else printf("BAD LUCK!\n");
14     }
15     return 0;   
16 }

 

Northcott Game

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4282    Accepted Submission(s): 1960

Problem Description

　　Tom和Jerry正在玩一种Northcott游戏，可是Tom老是输，因此他怀疑这个游戏是不是有某种必胜策略，郁闷的Tom现在向你求救了，你能帮帮他么？
游戏规则是这样的：
　　如图所示，游戏在一个n行m列（1 ≤ n ≤ 1000且2 ≤ m ≤ 100）的棋盘上进行，每行有一个黑子（黑方）和一个白子（白方）。执黑的一方先行，每次玩家可以移动己方的任何一枚棋子到同一行的任何一个空格上，当然这过程中不许越过该行的敌方棋子。双方轮流移动，直到某一方无法行动为止，移动最后一步的玩家获胜。Tom总是先下（黑方）。图1是某个初始局面，图二是Tom移动一个棋子后的局面（第一行的黑子左移两步）。



图1



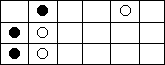
图2

 

 

Input

　　输入数据有多组。每组数据第一行为两个整数n和m，由空格分开。接下来有n行，每行两个数Ti，Ji (1 ≤ Ti, Ji ≤ m)分别表示Tom和Jerry在该行棋子所处的列数。
　　注意：各组测试数据之间有不定数量的空行。你必须处理到文件末。

 

 

Output

对于每组测试数据输出一行你的结果。如果当前局面下Tom有必胜策略则输出“I WIN!”，否则输出“BAD LUCK!”。

 

 

Sample Input

3 6 4 5 1 2 1 2 3 6 4 5 1 3 1 2

 

 

Sample Output

BAD LUCK! I WIN!