优化与神经网络

Posted 2020-11-09 cbfstudy

优化与神经网络

计算机视觉

1.优化的概念

首先上一节说了一个损失函数，用这个计算出来的得分来进行 评测 我们的模型好还是不好。分数越低模型越好。那么我们 做一系列工作的目的就是想达到损失函数的最小值。

这是一个类比的地方。假设我们在山里：类似有一个损失函数，我们处在山里的某个位置：类似我们的损失函数有个普通的值，我们想要达到山谷：类似想要得到最小的损失函数。
如何做上面的过程呢？
方法1：Random Search

mark text随机选择一些权重计算损失函数。类似山里：随机处于一些位置看这个位置是不是山谷。

方法2： Random Local Search

从一个随机的W开始，然后生成一个随机扰动，aW，每次对W+aW 计算损失值，如果损失值变小了，就更新这个W。

方法3 ： Follow the slope

沿着斜坡的方向走。在 损失函数里就是 沿着梯度的方向。（比如二次函数沿着梯度往最低点前进）
关于梯度有2种方法

Numerical gradient（数值梯度）: approximate, slow, easy to write 近似，慢，容易写代码
Analytic gradient:（解析梯度） exact, fast, error-prone
数值梯度其实就是利用差分的一种近似，需要计算值。比较麻烦。
比如二维下的梯度的近似算法。

解析梯度就是常见的通过伟大的数学家发明的公式。我们手算出来表达式，写到代码里，所以算的快，准确。

2.通过计算单元 理解BP反向传播算法

1.例子F(x,y,z)=(x+y)z

enter description here

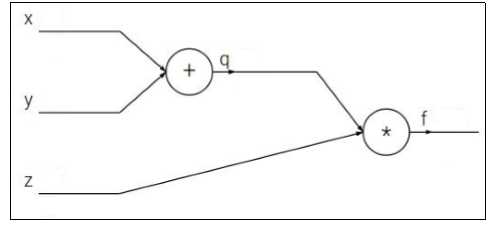
很好玩，就像堆积木一步步的。x,y做加法就把xy连到一个+的计算单元上。比较类似电路的与或非门？！先用计算单元的方式表示出这个损失。让后我们一步步的想着优化。
假定初始值：x=-2,y=5,z=-4。经过计算q=x+y=3 ,q * z=-12

1. 整个计算图最右端流出的是f(x,y,z)。用流出的f对f求导得到1。作为第一个上游梯度传入 最后一个计算单元。
2. 乘法单元，计算关于z和q的梯度。利用链式法则，得出，得出了f关于q和z的梯度。关于q的梯度，作为上游梯度流入产生q的计算单元。
3. ，链式法则，
4. 得到了关于参数x,y,z的梯度。就可以更新啦！！！

2.代码的时候小经验

1. 保存中间变量的值。类似于保存上面例子的q的值，方面bp的时候直接用。
2. 模块化。其实就是将一堆特别简单的计算单元封装一下成为一个单元。
3. 向量化。注意维度，不需要特别的记忆dw/db的公式，很容易推导出来

3.特殊门的梯度：

add gate: gradient distributor
max gate: gradient router
mul gate: gradient switche
Q:4096-d input vector what is the size of the Jacobian matrix?
[4096 x 4096!]
向量化的求导例子：

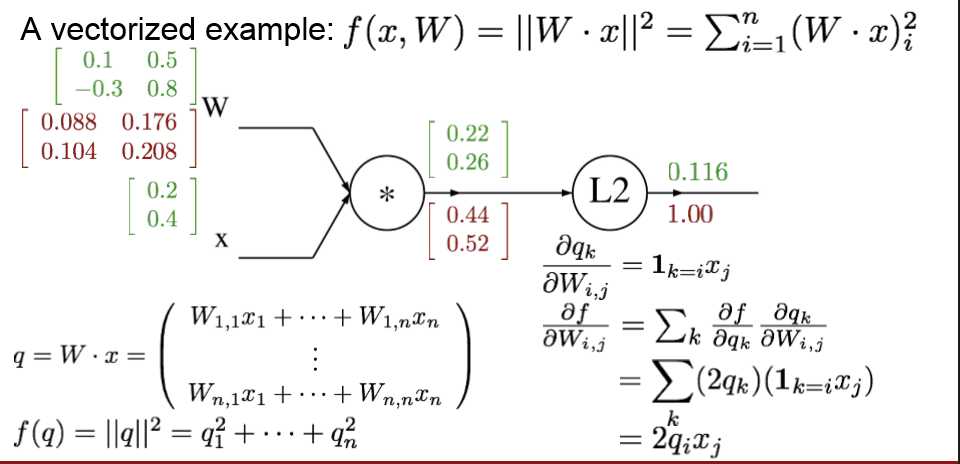
3 神经网络

enter description here

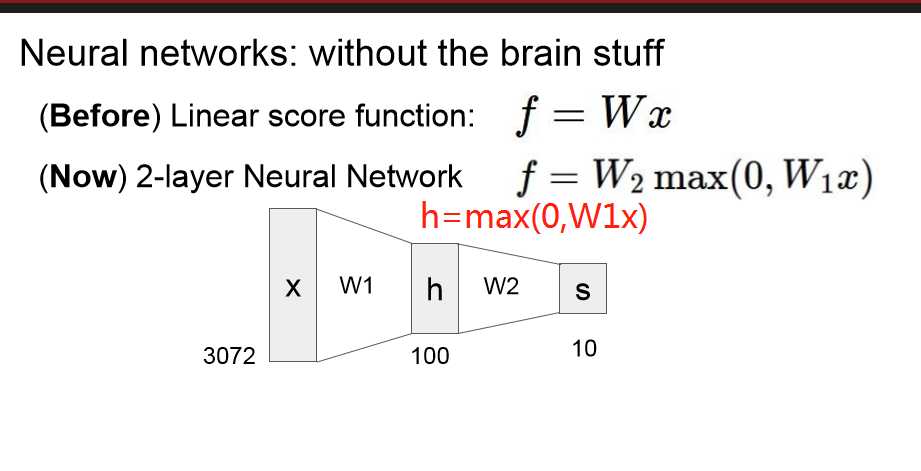
如图所示结构，通过bp更新参数。

4.卷积神经网络

1.Fully Connected Layer （全连接层）

enter description here

如上图，假定了输入的是大小是（1，3072），那么W的维度是C*3072,也就是W中每个参数都和元素进行了线性的运算。相当于线性的运算WX，然后用激活函数。

2.Convolution Layer（卷积层）

enter description here

原始图像大小，32323（长宽高（rgb通道数）），给定一个filter，这个filter的大小是553，filter的3必须要和上一层的输入的通道数一样，filter的大小通常是3，5，7。 然后从原始图像中也选取和filter一样大的区域与filter进行乘积（所有元素相乘相加）得到一个元素值，这个新计算出的元素值作为提取出来的特征。

3.如何在整个图像上进行卷积？

采用滑动窗口的方法

这个图简化成二维了，千万记得通道数。

3.卷积后维度的公式：

不进行填充的时候：(N-F)/stride +1
进行填充的时候：(N+2*pad-F)/stride +1
做0填充的 目的是保持和之前的大小一样。如果不做，会导致尺寸缩小的很快，丢失一些信息，只能用一些很少的值表示原来的信息。

4.卷积的参数个数问题：

Input volume: 32x32x3 10 5x5 filters with stride 1, pad 2
首先 55的卷积核有25个参数，10个的话是250个参数。不要忘记有3个通道，那么其实每个卷积核是 55*3的，所以说是750参数。这个时候有个陷阱，不要忘记每次卷积要加bias，所以760参数。

5.池化层：

通常的方式对于一个3*3区域进行一定的操作，比如max-pool，min-pool,mean-pool。池化的结果是大大的降低了维度，经常使用max-pool，效果较好（把每个元素看做神经的一个反应，最大的元素值 很好的代表了某个动作）。通常池化区域的选取之间不存在重叠的部分。

6.池化层参数:

和卷积一样。适当的考虑填充问题就行了。