tensorflow进阶篇-5(反向传播2)

Posted 2020-11-09 每天学习一点点

　　上面是一个简单的回归算法，下面是一个简单的二分值分类算法。从两个正态分布(N(-1,1)和N(3,1))生成100个数。所有从正态分布N(-1,1)生成的数据目标0；从正态分布N(3,1)生成的数据标为目标类1，模型算法通过sigmoid函数将这些生成的数据转换成目标类数据。换句话讲，模型算法是sigmoid(x+A)，其中，A是要拟合的变量，理论上A=-1。假设，两个正态分布的均值分别是m1和m2，则达到A的取值时，它们通过-(m1+m2)/2转换成到0等距离的值。

　　实现如下：

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import ops

ops.reset_default_graph()

# 创建计算图
sess = tf.Session()

# 生成数据，100个随机数x_vals：50个(-1,1)之间的随机数和50个(1,3)之间的随机数
# 以及100个目标数y_vals:50个0、50个1
x_vals = np.concatenate((np.random.normal(-1, 1, 50), np.random.normal(3, 1, 50)))
y_vals = np.concatenate((np.repeat(0., 50), np.repeat(1., 50)))
# 声明x_data、target占位符
x_data = tf.placeholder(shape=[1], dtype=tf.float32)
y_target = tf.placeholder(shape=[1], dtype=tf.float32)

# 声明变量A，(初始值为10附近，远离理论值-1)
A = tf.Variable(tf.random_normal(mean=10, shape=[1]))

# 实现sigmoid(x_data+A)，这里不必封装sigmoid函数，损失函数中会自动实现
my_output = tf.add(x_data, A)

# 为my_output、y_target添加一个维度
my_output_expanded = tf.expand_dims(my_output, 0)
y_target_expanded = tf.expand_dims(y_target, 0)

# 初始化所有变量
init = tf.initialize_all_variables()
sess.run(init)

# 添加损失函数，Sigmoid交叉熵损失函数。
# L = -actual * (log(sigmoid(pred))) - (1-actual)(log(1-sigmoid(pred)))
# or
# L = max(actual, 0) - actual * pred + log(1 + exp(-abs(actual)))
xentropy = tf.nn.sigmoid_cross_entropy_with_logits(logits=my_output_expanded,labels= y_target_expanded)

# 声明变量的优化器
my_opt = tf.train.GradientDescentOptimizer(0.05)
train_step = my_opt.minimize(xentropy)

# 训练,将损失值加入数组loss_batch
loss_batch = []
for i in range(1400):
    rand_index = np.random.choice(100)
    rand_x = [x_vals[rand_index]]
    rand_y = [y_vals[rand_index]]
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
    target=sess.run(xentropy, feed_dict={x_data: rand_x, y_target: rand_y})
    print(\'Step #\' + str(i + 1) + \' A = \' + str(sess.run(A)))
    print(\'Loss = \' + str(target))
    loss_batch.append(float(target))

plt.plot( loss_batch, \'r--\', label=\'Back Propagation\')
plt.legend(loc=\'upper right\', prop={\'size\': 11})
plt.show()

# 评估预测
predictions = []
for i in range(len(x_vals)):
    x_val = [x_vals[i]]
    prediction = sess.run(tf.round(tf.sigmoid(my_output)), feed_dict={x_data: x_val})
    predictions.append(prediction[0])

accuracy = sum(x == y for x, y in zip(predictions, y_vals)) / 100.
print(\'Ending Accuracy = \' + str(np.round(accuracy, 2)))

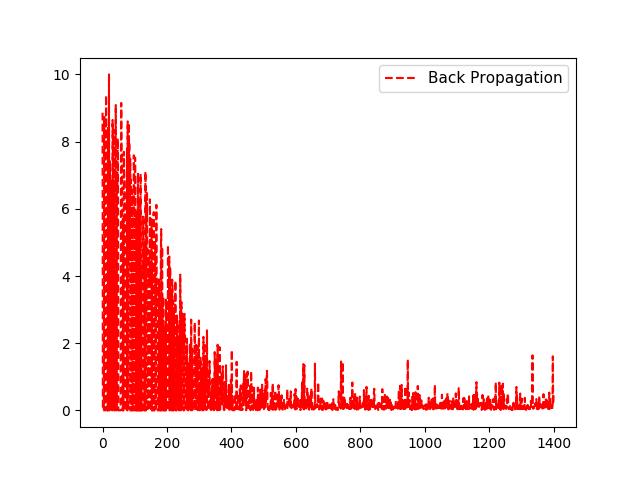
输出结果：

Step #1 A = [ 9.38409519]
Loss = [[ 8.86125183]]
Step #2 A = [ 9.38409519]
Loss = [[ 2.55701457e-06]]

.........

 

Step #1398 A = [-1.09940839]
Loss = [[ 1.60983551]]
Step #1399 A = [-1.09107065]
Loss = [[ 0.18104036]]
Step #1400 A = [-1.10927427]
Loss = [[ 0.44608194]]

Ending Accuracy = 0.96

对于损失函数看这里：tensorflow进阶篇-4(损失函数1)，tensorflow进阶篇-4(损失函数2)，tensorflow进阶篇-4(损失函数3)