神经网络的正反向传播算法推导

Posted 2020-11-08 艾克_塞伦特

1 正向传播

1.1 浅层神经网络

为简单起见，先给出如下所示的简单神经网络：

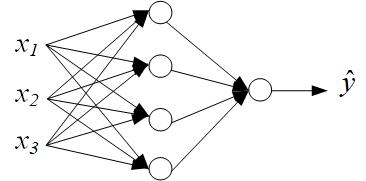
该网络只有一个隐藏层，隐藏层里有四个单元，并且只输入一个样本，该样本表示成一个三维向量，分别为为\\(x_1\\)，\\(x_2\\)和\\(x_3\\)。网络的输出为一个标量，用\\(\\hat{y}\\)表示。考虑该神经网络解决的问题是一个二分类的问题，把网络的输出解释为正样本的概率。比方说输入的是一张图片(当然图片不可能只用三维向量就可以表示，这里只是举个例子)，该神经网络去判断图片里面是否有猫，则\\(\\hat{y}\\)代表该图片中有猫的概率。另外，为衡量这个神经网络的分类表现，需要设置一个损失函数，针对二分类问题，最常用的损失函数是\\(log-loss\\)函数，该函数如下所示：

\\[L(y,\\hat{y}) = -y \\times log(\\hat{y}) - (1-y) \\times log(1-\\hat{y}) \\tag{1} \\]

上式只考虑一个样本的情况，其中\\(y\\)为真实值，\\(\\hat{y}\\)为输出的概率。

1.1.1 单样本的前向传播

我们把单个输入样本用向量表示为：

\\[\\boldsymbol{x} = \\left[ \\begin{matrix} x_1 \\\\ x_2 \\\\ x_3 \\end{matrix} \\right] \\tag{2} \\]

那么对于隐藏层中的第一个单元，如果不考虑激活函数，则其输出可以表示为：

\\[z^{[1]}_1 = \\boldsymbol{w}^{[1]^T}_1\\boldsymbol{x} + b^{[1]}_1 \\tag{3} \\]

上式中，字母右上角的方括号中的数字代表这是神经网络的第几层，如果把输入层看作是第0层的话，那么这里的隐藏层就是第一层，字母的下标代表该层的第几个单元。\\(\\boldsymbol{w}^{[1]}_1\\)是权重向量，即给输入向量的每个元素一个权重，这些权重组合起来就形成了\\(\\boldsymbol{w}^{[1]}_1\\)向量，把向量和其权重作点乘，再加上一个偏置标量\\(b^{[1]}_1\\)，就得到了该神经元的输出\\(z^{[1]}_1\\)。

同理可得隐藏层剩余三个单元的输出为：

\\[z^{[1]}_2 = \\boldsymbol{w}^{[1]^T}_2\\boldsymbol{x} + b^{[1]}_2 \\tag{4} \\]

\\[z^{[1]}_3 = \\boldsymbol{w}^{[1]^T}_3\\boldsymbol{x} + b^{[1]}_3 \\tag{5} \\]

\\[z^{[1]}_4 = \\boldsymbol{w}^{[1]^T}_4\\boldsymbol{x} + b^{[1]}_4 \\tag{6} \\]

但是对于每一个神经单元，其输出必须有一个非线性激活函数，否则神经网络的输出就是输入向量的线性运算得到的结果，这样会大大限制神经网络的能力。激活函数的种类有很多种，一般来说选用激活函数要视具体的应用情况而定，这里选用最常用的\\(sigmoid\\)激活函数。注：在1.2节之前，所有神经层都只用\\(sigmoid\\)激活函数。该函数的表达式如下：

\\[{\\sigma}(z) = \\frac{1}{1+e^{-z}} \\tag{7} \\]

sigmoid函数的导数和原函数的关系如下，这在具体进行计算的时候经常会用到：

\\[{\\sigma}^{\'}(z) = {\\sigma}(z)(1-\\sigma(z)) \\tag{8} \\]

所以上面神经单元的计算结果需要再输入到sigmoid函数进行计算:

\\[a^{[1]}_1 = {\\sigma}(z^{[1]}_1) \\tag{9} \\]

\\[a^{[1]}_2 = {\\sigma}(z^{[1]}_2) \\tag{10} \\]

\\[a^{[1]}_3 = {\\sigma}(z^{[1]}_3) \\tag{11} \\]

\\[a^{[1]}_4 = {\\sigma}(z^{[1]}_4) \\tag{12} \\]

上面的四个式子中，上下角标的意义不变，用字母\\(a\\)来表示激活函数的输出结果是因为单词activation（激活）的首字母为a。
至此已经完成了从输入向量到隐藏层的输出计算，现在再计算最后一步，即从隐藏层到最终的输出。

和上述的计算过程一样，只不过这次是把隐藏层的输出作为输出层的输入，先把\\(a^{[1]}_1\\)到\\(a^{[1]}_4\\)组成一个向量：

\\[\\boldsymbol{a^{[1]}} = \\left[ \\begin{matrix} a^{[1]}_1 \\\\ a^{[1]}_2 \\\\ a^{[1]}_3 \\\\ a^{[1]}_4 \\end{matrix} \\right] \\tag{13} \\]

再把该向量和对应的权重向量作点乘，最后加上一个偏置标量：

\\[z^{[2]}_1 = \\boldsymbol{w}^{[2]^T}_1\\boldsymbol{a^{[1]}} + b^{[2]}_1 \\tag{14} \\]

输出层是隐藏层的下一层，所以方括号的标注变成了2；由于输出只有一个神经单元，所以上式可省略下标：

\\[z^{[2]} = \\boldsymbol{w}^{[2]^T}\\boldsymbol{a^{[1]}} + b^{[2]} \\tag{15} \\]

同样地，把上面的结果输入到\\(sigmoid\\)函数里面，得到最终的输出结果：

\\[\\hat{y} = a^{[2]} = {\\sigma}(z^{[2]}) \\tag{16} \\]

单样本在神经网络的前向传播计算到这里基本已经结束了，但是上面的计算过程显得不是那么紧凑，比如在计算隐藏层的第一到第四个神经单元输出结果的时候，我们是按顺序一个一个计算的，这样的计算如果在具有非常多的神经单元的情况下，会导致最终的计算速度很慢，不高效。所以我们应当把上述的计算过程向量化，不仅使得公式更加简洁明了，而且会大大加快运算速度(很多软件包针对向量计算做了优化)。向量化的过程叙述如下：

首先考虑隐藏层中的权重向量，这些向量可以按行整合成一个矩阵：

\\[\\boldsymbol{W^{[1]}} = \\left[ \\begin{matrix} ...\\boldsymbol{w}^{[1]^T}_1 ...\\\\ ...\\boldsymbol{w}^{[1]^T}_2 ...\\\\ ...\\boldsymbol{w}^{[1]^T}_3 ...\\\\ ...\\boldsymbol{w}^{[1]^T}_4 ... \\end{matrix} \\right] \\tag{17} \\]

同样地，标量\\(b^{[1]}_1\\)到\\(b^{[1]}_4\\), \\(z^{[1]}_1\\)到\\(z^{[1]}_4\\)以及\\(a^{[1]}_1\\)到\\(a^{[1]}_4\\)可以分别组成一个列向量：

\\[\\boldsymbol{b^{[1]}} = \\left[ \\begin{matrix} b^{[1]}_1\\\\ b^{[1]}_2 \\\\ b^{[1]}_3 \\\\ b^{[1]}_4 \\end{matrix} \\right] \\tag{18} \\]

\\[\\boldsymbol{z^{[1]}} = \\left[ \\begin{matrix} z^{[1]}_1\\\\ z^{[1]}_2 \\\\ z^{[1]}_3 \\\\ z^{[1]}_4 \\end{matrix} \\right] \\tag{19} \\]

\\[\\boldsymbol{a^{[1]}} = \\left[ \\begin{matrix} a^{[1]}_1\\\\ a^{[1]}_2 \\\\ a^{[1]}_3 \\\\ a^{[1]}_4 \\end{matrix} \\right] \\tag{20} \\]

这样，式(3)-式(6)可以用向量形式表达为：

\\[\\boldsymbol{z^{[1]}} = \\boldsymbol{W^{[1]}}\\boldsymbol{x} + \\boldsymbol{b^{[1]}} \\tag{21} \\]

其中\\(\\boldsymbol{W^{[1]}}\\)是一个\\(4\\times3\\)的矩阵，\\(\\boldsymbol{x}\\)向量为\\(3\\times1\\)，二者相乘得到的维数为\\(4\\times1\\)，刚好和\\(\\boldsymbol{b^{[1]}}\\)、\\(\\boldsymbol{z^{[1]}}\\)的维数相同。

然后计算\\(\\boldsymbol{a^{[1]}}\\):

\\[\\boldsymbol{a^{[1]}} = {\\sigma}(\\boldsymbol{z^{[1]}}) \\tag{22} \\]

\\({\\sigma}(\\boldsymbol{z^{[1]}})\\)的计算方式是，对向量\\(\\boldsymbol{z^{[1]}}\\)中的每一个元素，依次输入到\\(sigmoid\\)函数中计算，最后将结果整合成一个向量。

同样可以把输出层的计算过程用向量表示：

\\[\\boldsymbol{z^{[2]}} = \\boldsymbol{W^{[2]}}\\boldsymbol{\\boldsymbol{a^{[1]}}} + \\boldsymbol{b^{[2]}} \\tag{23} \\]

\\[\\boldsymbol{a^{[2]}} = {\\sigma}(\\boldsymbol{z^{[2]}}) \\tag{24} \\]

其中\\(\\boldsymbol{W^{[2]}}\\)是一个\\(1\\times4\\)的矩阵，\\(\\boldsymbol{a^{[1]}}\\)向量为\\(4\\times1\\)，二者相乘得到的维数为\\(1\\times1\\)，\\(\\boldsymbol{b^{[2]}}\\)也是一个标量，所以最后的结果肯定是一个标量，也就是\\(\\boldsymbol{a^{[2]}}\\)了，这里将\\(\\boldsymbol{a^{[2]}}\\)和\\(\\boldsymbol{b^{[2]}}\\)加粗是为了和向量表示相统一，实际上它并不是一个向量，除非输出的数值不止一个。

从上面的计算过程也可以总结出，权重矩阵\\(\\boldsymbol{W^{[l]}}\\)的维数是\\(n^{[l]}\\times n^{[l-1]}\\)，偏置向量\\(\\boldsymbol{b^{[l]}}\\)的维数是\\(n^{[l]}\\times 1\\)，其中\\(l\\)代表某一层，\\(l-1\\)则为上一层，\\(n^{[l]}\\)代表该层的神经单元数。

综上所述，式(21)-式(24)用向量化的方式完成了单样本输入神经网络的计算，总共就四个表达式，看起来十分简洁。

1.1.2 多样本的前向传播

在上面的例子中，我们使用的是单样本的前向传播过程，实际应用中是不可能只有一个样本的，会有很多个样本，那么针对多样本的前向传播过程又是怎么样的呢？其实过程是和单样本的过程是一样的，只不过是把输入的单个向量\\(\\boldsymbol{x}\\)变成了矩阵\\(\\boldsymbol{X}\\)，该矩阵是把输入的每一个样本向量按列排序得到的，下面考虑m个样本，式(25)中右上角的圆括号中的数字代表样本编号：

\\[\\boldsymbol{X} = \\left[ \\begin{matrix} \\vdots & \\vdots & & \\vdots \\\\ \\boldsymbol{x^{(1)}} & \\boldsymbol{x^{(2)}} & \\cdots & \\boldsymbol{x^{(m)}} \\\\ \\vdots & \\vdots & & \\vdots \\end{matrix} \\right] \\tag{25} \\]

那么式(21)-式(24)拓展到m个样本，就可以改写为：

\\[\\boldsymbol{Z^{[1]}} = \\boldsymbol{W^{[1]}}\\boldsymbol{X} + \\boldsymbol{B^{[1]}} \\tag{26} \\]

\\[\\boldsymbol{A^{[1]}} = {\\sigma}(\\boldsymbol{Z^{[1]}}) \\tag{27} \\]

\\[\\boldsymbol{Z^{[2]}} = \\boldsymbol{W^{[2]}}\\boldsymbol{\\boldsymbol{A^{[1]}}} + \\boldsymbol{B^{[2]}} \\tag{28} \\]

\\[\\boldsymbol{A^{[2]}} = {\\sigma}(\\boldsymbol{Z^{[2]}}) \\tag{29} \\]

式(26)-式(29)相对于式(21)-式(24)唯一的变化就是把z、a和b由向量表示转变为矩阵表示，具体的来看，比方说\\(\\boldsymbol{Z^{[1]}}\\)、\\(\\boldsymbol{B^{[1]}}\\)和\\(\\boldsymbol{A^{[1]}}\\)可类似于\\(\\boldsymbol{X}\\)展开为：

\\[\\boldsymbol{Z^{[1]}} = \\left[ \\begin{matrix} \\vdots & \\vdots & & \\vdots \\\\ \\boldsymbol{z^{(1)^{[1]}}} & \\boldsymbol{z^{(2)^{[1]}}} & \\cdots & \\boldsymbol{z^{(m)^{[1]}}} \\\\ \\vdots & \\vdots & & \\vdots \\end{matrix} \\right] \\tag{30} \\]

\\[\\boldsymbol{B^{[1]}} = \\left[ \\begin{matrix} \\vdots & \\vdots & & \\vdots \\\\ \\boldsymbol{b^{(1)^{[1]}}} & \\boldsymbol{b^{(2)^{[1]}}} & \\cdots & \\boldsymbol{b^{(m)^{[1]}}} \\\\ \\vdots & \\vdots & & \\vdots \\end{matrix} \\right] \\tag{31} \\]

\\[\\boldsymbol{A^{[1]}} = \\left[ \\begin{matrix} \\vdots & \\vdots & & \\vdots \\\\ \\boldsymbol{a^{(1)^{[1]}}} & \\boldsymbol{a^{(2)^{[1]}}} & \\cdots & \\boldsymbol{a^{(m)^{[1]}}} \\\\ \\vdots & \\vdots & & \\vdots \\end{matrix} \\right] \\tag{32} \\]

如果觉得矩阵表示较为抽象，就可以应用这种展开方式方便理解。另外要注意，对于上面的矩阵\\(\\boldsymbol{B^{[1]}}\\)，其中的各个列向量\\(\\boldsymbol{b^{(1)^{[1]}}}\\)和\\(\\boldsymbol{b^{(2)^{[1]}}}\\)等等，其实是完全一样的，就是同一个列向量重复地排了\\(m\\)列，正如权重矩阵\\(\\boldsymbol{W^{[l]}}\\)不会随着样本的个数变化一样，偏置向量也是不会随着样本的不同而不同的。总而言之，对于同一个神经层，权重矩阵和偏置向量对于所有样本相同。从中可见式(26)-式(29)的维数也是正确的，例如式(26)中，\\(\\boldsymbol{W^{[1]}}\\)维数是\\(4\\times3\\),\\(\\boldsymbol{X}\\)的维数是\\(3\\times m\\),二者相乘的维数是\\(4\\times m\\)，而\\(\\boldsymbol{B^{[1]}}\\)以及\\(\\boldsymbol{Z^{[1]}}\\)的维数均是\\(4\\times m\\)，所以式(26)在维度上完全正确，余下的几个式子的维数分析同理。最后输出的是m个样本的计算结果：\\(\\boldsymbol{A^{[2]}}\\),它是把每个样本单独输出的结果按列排列得到，这和之前所有样本均按列排列的方式是一致的。至此也完成了m个样本在浅层神经网络的正向传播过程。

1.2 深层神经网络

利用浅层神经网络的分析结果，我们很容易把正向传播过程推广到深层神经网络上，即不再像本文开始提出的那种只有一个隐藏层并且只有4个隐藏神经单元的神经网络，可以有很多个隐藏层，每个隐藏层也可以有很多个神经单元，也不再限定输入的是一个三维向量，输入的可以为任意维向量，当然，每个样本的向量维度必须一致，否则神经网络没法工作,同时网络的输出也可不限定为一个数值，可以输出一个向量以适应多分类的任务，即一个样本会有多个标签，输出向量表示该样本属于这些标签的概率值。最后作为一般概括，也不指定具体的激活函数，即激活函数在这里用\\(g^{[l]}(x)\\)表示。这样，我们可以把整个正向传输过程浓缩成：

\\[\\boldsymbol{Z^{[l]}} = \\boldsymbol{W^{[l]}}\\boldsymbol{A^{[l-1]}} + \\boldsymbol{b^{[l]}} \\tag{33} \\]

\\[\\boldsymbol{A^{[l]}} = g^{[l]}(\\boldsymbol{Z^{[l]}}) \\tag{34} \\]

上式中某一层用\\(l\\)表示，它的上一层用\\(l-1\\)来表示，这里规定输入层\\(l=0\\),第一个隐藏层\\(l=1\\)，后面以此类推，即有\\(1 \\leq l \\leq N\\),\\(N\\)为输出层编号。所以上面两个式子的计算过程就是输入上一层计算的\\(\\boldsymbol{A^{[l-1]}}\\),再输出本层的\\(\\boldsymbol{A^{[l]}}\\)，一直持续计算到输出层，最后得到计算的最终结果。需要注意的一点是对于第一个隐藏层，它的输入就是样本矩阵，也就是\\(\\boldsymbol{A^{[0]}} = \\boldsymbol{X}\\)。注意到式(33)我们没有用大写的\\(\\boldsymbol{B^{[l]}}\\)来代表偏置矩阵，而是用了小写的向量记法，代表的是一个列向量，这是为了后续反向传播推导的方便，但是我们心里应该明白，这里一个矩阵和一个向量相加，相加的方法是矩阵的每一列分别和该列向量相加，这样就和原大写的矩阵相加结果相同，因为前面已经指出，矩阵\\(\\boldsymbol{B^{[l]}}\\)就是单个列向量扩展\\(m\\)列得到的。

最后再来总结式(33)-式(34)中每个元素的维数，根据浅层神经网络的推导，我们也很容易把结论扩展到深层神经网络里面。以\\(n^{[l]}\\)表示该层的神经单元的个数(输入层\\(n^{[0]}\\)等于输入样本矩阵的行数，即单个样本向量的元素个数),m表示样本个数，则结论如下：

\\[\\boldsymbol{W^{[l]}} \\in \\mathbb{R}^{n^{[l]} \\times n^{[l-1]}} \\tag{35} \\]

\\[\\boldsymbol{b^{[l]}} \\in \\mathbb{R}^{n^{[l]} \\times 1} \\tag{36} \\]

\\[\\boldsymbol{Z^{[l]}} \\in \\mathbb{R}^{n^{[l]} \\times m} \\tag{37} \\]

\\[\\boldsymbol{A^{[l]}} \\in \\mathbb{R}^{n^{[l]} \\times m} \\tag{38} \\]

2 反向传播

现在来考虑反向传播的过程，该过程是一个不断迭代的过程，目的是寻找使得损失函数最小的参数，即每一个神经层的权重矩阵和偏置向量的数值。首先考虑单个样本在深层神经网络的反向传播的情况。

2.1 单样本的反向传播

计算反向传播的过程，我们首先要定义一个损失函数，为了不失一般性，这里用\\(L(\\boldsymbol{y}, \\boldsymbol{\\hat y})\\)表示损失函数，其中\\(\\boldsymbol{y}\\)为样本的真实标签，\\(\\boldsymbol{\\hat y}\\)为样本在神经网络中的计算结果。损失函数应当越小越好，越小就代表我们计算出的结果和样本的真实标签越接近。为和前面的章节相连贯，接下来我们考虑的是作为分类任务用的神经网络，即每一层包括输出层都会有一个激活函数，注意如果是回归任务，输出层是不需要激活函数的，因为激活函数会把输出结果限定在一个范围内，这对回归任务并不适用。我们记作\\(g(x)^{[l]}\\),\\(l\\)代表某一层。

针对单个样本，可记作:

\\[\\boldsymbol{a^{[0]}} = \\boldsymbol{x} = \\left[ \\begin{matrix} x_1 \\\\ x_2 \\\\ \\vdots \\\\ x_{n^{[0]}} \\end{matrix} \\right] \\tag{39} \\]

\\(n^{[l]}\\)表示\\(l\\)层的神经单元的个数，输入层的\\(l\\)记作0。那么后面的计算就可利用下面两个式子反复进行，其中\\(1\\leq l \\leq N\\)，N为输出层编号。一直进行到输出层得出结果：

\\[\\boldsymbol{z^{[l]}} = \\boldsymbol{W^{[l]}}\\boldsymbol{a^{[l-1]}} + \\boldsymbol{b^{[l]}} \\tag{40} \\]

\\[\\boldsymbol{a^{[l]}} = g^{[l]}(\\boldsymbol{z^{[l]}}) \\tag{41} \\]

假设神经网络一共有N层，我们则把最后的输出结果记作\\(\\boldsymbol{a^{[N]}}\\)，也就是\\(\\boldsymbol{\\hat{y}}\\)。利用损失函数最终得到损失值，我们的任务就是最小化这个数值，如何最小化？那么就必须调节参数\\(\\boldsymbol{W^{[l]}}\\)和\\(\\boldsymbol{b^{[l]}}\\)，这时候就需要用到反向传播算法了，即正向传播计算的是神经网络的输出值，而反向传播则计算修改后的网络参数，不断地进行正向反向传播，每一个正反来回都对这两个参数进行更新，再计算神经网络在参数更新后的损失值，和原来的损失值作比较，变小了就继续进行参数更新，反之则考虑是否停止参数更新，结束神经网络的计算。参数更新的过程如下所示，其中\\(1\\leq l\\leq N\\)：

\\[\\boldsymbol{W^{[l]}} = \\boldsymbol{W^{[l]}} - \\alpha \\times d\\boldsymbol{W^{[l]}} \\tag{42} \\]

\\[\\boldsymbol{b^{[l]}} = \\boldsymbol{b^{[l]}} - \\alpha \\times d\\boldsymbol{b^{[l]}} \\tag{43} \\]

式中，\\(d\\boldsymbol{W^{[l]}}\\)和\\(d\\boldsymbol{b^{[l]}}\\)分别代表损失函数对这二者的求偏导的结果，即：

\\[d{\\boldsymbol{W^{[l]}}} = \\frac{\\partial L}{\\partial{\\boldsymbol{W^{[l]}}}} \\tag{44} \\]

\\[d{\\boldsymbol{b^{[l]}}} = \\frac{\\partial L}{\\partial{\\boldsymbol{b^{[l]}}}} \\tag{45} \\]

而\\(\\alpha\\)代表参数更新的步长，称作学习率。问题的关键就在于怎么求出\\(d\\boldsymbol{W^{[l]}}\\)和\\(d\\boldsymbol{b^{[l]}}\\)，这时候就需要考虑导数的链式法则了。反向传播的起点在最后一步，即损失函数这一步，从输出层开始再一层一层地往回计算，所以先考虑损失函数\\(L(\\boldsymbol{a^{[N]}} \\boldsymbol{\\hat y})\\)和输出层参数，即先计算出\\(d\\boldsymbol{W^{[N]}}\\)和\\(d\\boldsymbol{b^{[N]}}\\)，先考虑前者，根据链式法则，很容易得出下式：

\\[\\begin{align*} d{\\boldsymbol{W^{[N]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{W^{[N]}}}} \\\\ &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}} \\frac{\\partial{\\boldsymbol{a^{[N]}}}}{\\partial{\\boldsymbol{W^{[N]}}}} \\\\ &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}} \\frac{\\partial{\\boldsymbol{a^{[N]}}}}{\\partial{\\boldsymbol{z^{[N]}}}} \\frac{\\partial{\\boldsymbol{z^{[N]}}}}{\\partial{\\boldsymbol{W^{[N]}}}} \\end{align*} \\tag{46} \\]

可见计算\\(d{\\boldsymbol{W^{[N]}}}\\)共需三步，即分别计算\\(\\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}}\\),\\(\\frac{\\partial{\\boldsymbol{a^{[N]}}}}{\\partial{\\boldsymbol{z^{[N]}}}}\\)和\\(\\frac{\\partial{\\boldsymbol{z^{[N]}}}}{\\partial{\\boldsymbol{W^{[N]}}}}\\)，然后相乘即可。
首先\\(\\boldsymbol{a^{[N]}}\\)求偏导得到：

\\[d{\\boldsymbol{a^{[N]}}} = \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}} \\tag{47} \\]

式(47)的具体计算结果依赖于具体的损失函数L，由于我们作一般化考虑，所以到此为止，不再继续计算下去。然后根据式(41)又有：

\\[\\frac{\\partial{\\boldsymbol{a^{[N]}}}}{\\partial{\\boldsymbol{z^{[N]}}}} = {g^{[N]}}^{\\prime}(\\boldsymbol{z^{[N]}}) \\tag{48} \\]

再根据式(40),得到：

\\[\\frac{\\partial{\\boldsymbol{z^{[N]}}}}{\\partial{\\boldsymbol{W^{[N]}}}} = \\boldsymbol{a^{[N-1]}} \\tag{49} \\]

综合式(47)-式(48)，可以得到：

\\[\\begin{align*} d{\\boldsymbol{z^{[N]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}}\\frac{\\partial{\\boldsymbol{a^{[N]}}}} {\\partial{\\boldsymbol{z^{[N]}}}} \\\\ &= d{\\boldsymbol{a^{[N]}}}{g^{[N]}}^{\\prime}(\\boldsymbol{z^{[N]}}) \\end{align*} \\tag{50} \\]

但是要注意的是，式(50)并不正确，因为维度不匹配。各元素维度为：

\\[d{\\boldsymbol{z^{[N]}}} \\in \\mathbb{R}^{n[N]\\times 1} \\tag{51} \\]

\\[d{\\boldsymbol{a^{[N]}}} \\in \\mathbb{R}^{n[N]\\times 1} \\tag{52} \\]

\\[{g^{[N]}}^{\\prime}(\\boldsymbol{z^{[N]}}) \\in \\mathbb{R}^{n[N]\\times 1} \\tag{53} \\]

所以改写式(50)使其满足正确的维度：

\\[\\begin{align*} d{\\boldsymbol{z^{[N]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}}\\frac{\\partial{\\boldsymbol{a^{[N]}}}} {\\partial{\\boldsymbol{z^{[N]}}}} \\\\ &= d{\\boldsymbol{a^{[N]}}}\\circ{g^{[N]}}^{\\prime}(\\boldsymbol{z^{[N]}}) \\end{align*} \\tag{54} \\]

式(54)中的空心圆点代表这两个向量对应元素进行相乘。再把式(54)和式(49)联立，可得：

\\[d{\\boldsymbol{W^{[N]}}} = d{\\boldsymbol{z^{[N]}}}\\boldsymbol{a^{[N-1]}} \\tag{55} \\]

同样地，式(55)也不满足正确的维度。各元素的维度为：

\\[d{\\boldsymbol{z^{[N]}}} \\in \\mathbb{R}^{n[N]\\times 1} \\tag{56} \\]

\\[\\boldsymbol{a^{[N-1]}} \\in \\mathbb{R}^{n[N]\\times 1} \\tag{57} \\]

\\[d{\\boldsymbol{W^{[N]}}} \\in \\mathbb{R}^{n[N]\\times n[N-1]} \\tag{58} \\]

改写式(55)使其满足正确的维度：

\\[d{\\boldsymbol{W^{[N]}}} = d{\\boldsymbol{z^{[N]}}}\\boldsymbol{{a^{[N-1]}}^T} \\tag{59} \\]

至此已经完成了\\(d{\\boldsymbol{W^{[N]}}}\\)的计算，那么还剩下\\(d{\\boldsymbol{b^{[N]}}}\\)还没有计算，计算它就简单多了，因为根据式(40)，\\(d{\\boldsymbol{b^{[N]}}}\\)就等于\\(d{\\boldsymbol{z^{[N]}}}\\),所以有：

\\[\\begin{align*} d{\\boldsymbol{b^{[N]}}} &= d{\\boldsymbol{z^{[N]}}} \\\\ &= d{\\boldsymbol{a^{[N]}}}\\circ{g^{[N]}}^{\\prime}(\\boldsymbol{z^{[N]}}) \\end{align*} \\tag{60} \\]

\\(d{\\boldsymbol{W^{[N]}}}\\)和\\(d{\\boldsymbol{b^{[N]}}}\\)都计算出来之后，就可以利用式(42)-式(43)更新参数了：

\\[\\boldsymbol{W^{[N]}} = \\boldsymbol{W^{[N]}} - \\alpha \\times d\\boldsymbol{W^{[N]}} \\tag{61} \\]

\\[\\boldsymbol{b^{[N]}} = \\boldsymbol{b^{[N]}} - \\alpha \\times d\\boldsymbol{b^{[N]}} \\tag{62} \\]

下面再来考虑\\(d{\\boldsymbol{W^{[N-1]}}}\\)和\\(d{\\boldsymbol{b^{[N-1]}}}\\)的计算，即输出层的上一层，也就是最后一个隐藏层的参数。事实上，根据式(59)-式(60),就可以进行计算了，不过是把N换成N-1而已，但是这里有个问题是\\(d{\\boldsymbol{a^{[N-1]}}}\\)没法得出，所以关键就是把它的表达式给求出来。根据式(40)-式(41)，再应用链式法则，不难得到：

\\[\\begin{align*} d{\\boldsymbol{a^{[N-1]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N-1]}}}} \\\\ &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}} \\frac{\\partial{\\boldsymbol{a^{[N]}}}}{\\partial{\\boldsymbol{z^{[N]}}}} \\frac{\\partial{\\boldsymbol{z^{[N]}}}}{\\partial{\\boldsymbol{a^{[N-1]}}}} \\end{align*} \\tag{63} \\]

式(63)可整理如下：

\\[\\begin{align*} d{\\boldsymbol{a^{[N-1]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}} \\frac{\\partial{\\boldsymbol{a^{[N]}}}}{\\partial{\\boldsymbol{z^{[N]}}}} \\frac{\\partial{\\boldsymbol{z^{[N]}}}}{\\partial{\\boldsymbol{a^{[N-1]}}}} \\\\ &= d{\\boldsymbol{z^{[N]}}}{\\boldsymbol{W^{[N]}}} \\end{align*} \\tag{64} \\]

式(64)的维度也是有问题的，整理如下，使得元素维度匹配：

\\[\\begin{align*} d{\\boldsymbol{a^{[N-1]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}} \\frac{\\partial{\\boldsymbol{a^{[N]}}}}{\\partial{\\boldsymbol{z^{[N]}}}} \\frac{\\partial{\\boldsymbol{z^{[N]}}}}{\\partial{\\boldsymbol{a^{[N-1]}}}} \\\\ &= {\\boldsymbol{W^{[N]}}}^Td{\\boldsymbol{z^{[N]}}} \\end{align*} \\tag{65} \\]

目前为止，基本完成了单个样本的反向传播过程，主要过程、公式整理如下：

对于输出层有：

\\[d{\\boldsymbol{a^{[N]}}} = \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}} \\tag{66} \\]

\\[\\begin{align*} d{\\boldsymbol{z^{[N]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[N]}}}}\\frac{\\partial{\\boldsymbol{a^{[N]}}}} {\\partial{\\boldsymbol{z^{[N]}}}} \\\\ &= d{\\boldsymbol{a^{[N]}}}\\circ{g^{[N]}}^{\\prime}(\\boldsymbol{z^{[N]}}) \\end{align*} \\tag{67} \\]

\\[d{\\boldsymbol{W^{[N]}}} = d{\\boldsymbol{z^{[N]}}}\\boldsymbol{{a^{[N-1]}}^T} \\tag{68} \\]

\\[\\begin{align*} d{\\boldsymbol{b^{[N]}}} &= d{\\boldsymbol{z^{[N]}}} \\\\ &= d{\\boldsymbol{a^{[N]}}}\\circ{g^{[N]}}^{\\prime}(\\boldsymbol{z^{[N]}}) \\end{align*} \\tag{69} \\]

其中\\(d{\\boldsymbol{a^{[N]}}}\\)是可以直接利用损失函数进行求导计算得出，而对于其他神经层则需要利用链式法则来求出。设\\(h\\)为为任意隐藏层，即\\(1\\leq h \\leq N-1\\),则有：

\\[\\begin{align*} d{\\boldsymbol{a^{[h]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[h+1]}}}} \\frac{\\partial{\\boldsymbol{a^{[h+1]}}}}{\\partial{\\boldsymbol{z^{[h+1]}}}} \\frac{\\partial{\\boldsymbol{z^{[h+1]}}}}{\\partial{\\boldsymbol{a^{[h]}}}} \\\\ &= {\\boldsymbol{W^{[h+1]}}}^Td{\\boldsymbol{z^{[h+1]}}} \\end{align*} \\tag{70} \\]

\\[\\begin{align*} d{\\boldsymbol{z^{[h]}}} &= \\frac{\\partial L}{\\partial{\\boldsymbol{a^{[h]}}}}\\frac{\\partial{\\boldsymbol{a^{[h]}}}} {\\partial{\\boldsymbol{z^{[h]}}}} \\\\ &= d{\\boldsymbol{a^{[h]}}}\\circ{g^{[h]}}^{\\prime}(\\boldsymbol{z^{[h]}}) \\end{align*} \\tag{71} \\]

\\[d{\\boldsymbol{W^{[h]}}} = d{\\boldsymbol{z^{[h]}}}\\boldsymbol{{a^{[h-1]}}^T} \\tag{72} \\]

\\[\\begin{align*} d{\\boldsymbol{b^{[h]}}} &= d{\\boldsymbol{z^{[h]}}} \\\\ &= d{\\boldsymbol{a^{[h]}}}\\circ{g^{[h]}}^{\\prime}(\\boldsymbol{z^{[h]}}) \\end{align*} \\tag{73} \\]

最后的参数更新只需按照下面式子来进行即可，其中\\(1 \\leq l \\leq N\\)：

\\[\\boldsymbol{W^{[l]}} = \\boldsymbol{W^{[l]}} - \\alpha \\times d\\boldsymbol{W^{[l]}} \\tag{74} \\]

\\[\\boldsymbol{b^{[l]}} = \\boldsymbol{b^{[l]}} - \\alpha \\times d\\boldsymbol{b^{[l]}} \\tag{75} \\]

2.2 多样本的反向传播

考虑\\(m\\)个样本，各种符号表示以及解释参考式(25)-式(32)。损失函数则定义为所有样本损失值的平均值，即有如下定义：

\\[J(\\boldsymbol{W}, \\boldsymbol{b}) = \\frac{1}{m}\\Sigma^{m}_{i=1}L(\\boldsymbol{y^{(i)}}, \\boldsymbol{\\hat y^{(i)}}) \\tag{76} \\]

总的损失函数值是所有样本的损失值的平均，那么权值参数\\(\\boldsymbol{W^{[l]}}\\)和偏置参数\\(\\boldsymbol{b^{[l]}}\\)也应当是考虑了所有的样本计算后的平均。同样地，先考虑输出层的参数，利用式(66)-式(69)可得:

\\[d{\\boldsymbol{A^{[N]}}} = \\frac{\\partial J}{\\partial{\\boldsymbol{A^{[N]}}}} \\tag{77} \\]

\\[\\begin{align*} d{\\boldsymbol{Z^{[N]}}} &= \\frac{\\partial J}{\\partial{\\boldsymbol{A^{[N]}}}}\\frac{\\partial{\\boldsymbol{A^{[N]}}}} {\\partial{\\boldsymbol{z^{[N]}}}} \\\\ &= d{\\boldsymbol{A^{[N]}}}\\circ{g^{[N]}}^{\\prime}(\\boldsymbol{Z^{[N]}}) \\end{align*} \\tag{78} \\]

\\[d{\\boldsymbol{W^{[N]}}} = \\frac{1}{m}d{\\boldsymbol{Z^{[N]}}}\\boldsymbol{{A^{[N-1]}}^T} \\tag{79} \\]

\\[\\begin{align*} d{\\boldsymbol{b^{[N]}}} &= \\frac{1}{m}sum(d{\\boldsymbol{Z^{[N]}}},axis=1) \\\\ &= \\frac{1}{m}sum(d{\\boldsymbol{A^{[N]}}}\\circ{g^{[N]}}^{\\prime}(\\boldsymbol{Z^{[N]}}), axis=1) \\end{align*} \\tag{80} \\]

注意的是式(80)，列向量\\(d{\\boldsymbol{b^{[N]}}}\\)是通过\\(d{\\boldsymbol{Z^{[N]}}}\\)矩阵取每一行的平均值得到的，在直觉上也不难理解，矩阵\\(d{\\boldsymbol{Z^{[N]}}}\\)是每个样本的\\(d{\\boldsymbol{z^{[N]}}}\\)按列排列得到的，而\\(d{\\boldsymbol{b^{[N]}}}\\)需要对每个样本的\\(d{\\boldsymbol{b^{[N]}}}\\)求平均而得到，式(80)的做法正符合这一要求。至于式(78)只要将矩阵相乘的结果除以样本个数，这种做法可以将两个矩阵拆开来看，可以发现\\(d{\\boldsymbol{W^{[N]}}}\\)确实也是综合考虑了所有样本的\\(d{\\boldsymbol{W^{[N]}}}\\)，然后求平均得到，具体请自行操作体会。

对于所有隐藏层，对式(70)-式(73)进行同样的改动，即可获得相应结果。设\\(h\\)为为任意隐藏层，即\\(1\\leq h \\leq N-1\\)，则有：

\\[\\begin{align*} d{\\boldsymbol{A^{[h]}}} &= \\frac{\\partial J}{\\partial{\\boldsymbol{A^{[h+1]}}}} \\frac{\\partial{\\boldsymbol{A^{[h+1]}}}}{\\partial{\\boldsymbol{Z^{[h+1]}}}} \\frac{\\partial{\\boldsymbol{Z^{[h+1]}}}}{\\partial{\\boldsymbol{A^{[h]}}}} \\\\ &= {\\boldsymbol{W^{[h+1]}}}^Td{\\boldsymbol{Z^{[h+1]}}} \\end{align*} \\tag{81} \\]

\\[\\begin{align*} d{\\boldsymbol{Z^{[h]}}} &= \\frac{\\partial J}{\\partial{\\boldsymbol{A^{[h]}}}}\\frac{\\partial{\\boldsymbol{A^{[h]}}}} {\\partial{\\boldsymbol{Z^{[h]}}}} \\\\ &= d{\\boldsymbol{A^{[h]}}}\\circ{g^{[h]}}^{\\prime}(\\boldsymbol{Z^{[h]}}) \\end{align*} \\tag{82} \\]

\\[d{\\boldsymbol{W^{[h]}}} = \\frac{1}{m}d{\\boldsymbol{Z^{[h]}}}\\boldsymbol{{A^{[h-1]}}^T} \\tag{83} \\]

\\[\\begin{align*} d{\\boldsymbol{b^{[h]}}} &= \\frac{1}{m}sum(d{\\boldsymbol{Z^{[h]}}}, axis=1) \\\\ &= \\frac{1}{m}sum(d{\\boldsymbol{A^{[h]}}}\\circ{g^{[h]}}^{\\prime}(\\boldsymbol{Z^{[h]}}), axis=1) \\end{align*} \\tag{84} \\]

更新参数的方法同式(74)-式(75)。顺便提一下，在实际应用中，往往会在式(76)所示的损失函数后面加上一个正则化项，以防止过拟合。现在我们使用下式所示的损失函数：

\\[J(\\boldsymbol{W}, \\boldsymbol{b}) = \\frac{1}{m}\\Sigma^{m}_{i=1}L(\\boldsymbol{y^{(i)}}, \\boldsymbol{\\hat y^{(i)}}) + \\frac{\\lambda}{2m}\\Sigma^{l}_{l=1}||\\boldsymbol{W^{[l]}}||^2_F \\tag{85} \\]

其中：

\\[||\\boldsymbol{W^{[l]}}||^2_F = \\Sigma^{n[l]}_{i=1}\\Sigma^{n[l-1]}_{j=1}(\\boldsymbol{W^{[l]}_{ij}})^2 \\tag{86} \\]

即矩阵中每个元素的平方之和。这种矩阵范数称为Frobenius范数。正则化项中的\\(\\lambda\\)是正则化参数，这是一个超参数，需要在实验中进行调节，不断地尝试才能确定最好的\\(\\lambda\\)值。对于包含这种正则化项的反向传播又作如何处理？其实就是在\\(d{\\boldsymbol{W}}\\)的后面加上\\(\\frac{\\lambda}{m}\\boldsymbol{W}\\)即可,而\\(d{\\boldsymbol{b}}\\)参数不需要变化。式(79)和式(83)可分别改写为：

\\[d{\\boldsymbol{W^{[N]}}} = \\frac{1}{m}d{\\boldsymbol{Z^{[N]}}}\\boldsymbol{{A^{[N-1]}}^T}+\\frac{\\lambda}{m}\\boldsymbol{W^{[N]}} \\tag{87} \\]

\\[d{\\boldsymbol{W^{[h]}}} = \\frac{1}{m}d{\\boldsymbol{Z^{[h]}}}\\boldsymbol{{A^{[h-1]}}^T}+\\frac{\\lambda}{m}\\boldsymbol{W^{[h]}} \\tag{88} \\]

再利用式(74)-式(75)进行参数更新即可，可见加了正则化项之后，参数会比原来要小一点，因为多减去了\\(\\frac{\\lambda}{m}\\boldsymbol{W}\\)这一项。现在，神经网络的正反向传播算法基本推导完毕。

参考文献
吴恩达《深度学习》视频