第十三章——卷积神经网络（CNN）

Posted 2020-11-08 royhoo

本文介绍了卷积神经网络CNN的来源，CNN的不同模块（卷积层、池化层），以及如何使用TensorFlow实现CNN。最后介绍了一些优秀的CNN架构。

卷积神经网络（Convolutional neural networks，CNNs）来源于对大脑视觉皮层的研究，并于1980s开始应用于图像识别。现如今CNN已经在复杂的视觉任务中取得了巨大成功，比如图像搜索，自动驾驶，语言自动分类等等。同时CNN也应用于了其他领域，比如语音识别和自然语言处理。

13.1 视觉皮层机理

David H. Hubel和Torsten Wiesel于1958、1959年在猫的身上做实验，给出了关于视觉皮层结构的深刻见解（作者因此与1981年获得诺贝尔生物或医学奖）。特别的，他们指出视觉皮层的许多神经元具有一个很小的局部接受域（local receptive field）。也就是说，这种神经元只会对视野里一个有限的区域做出反应（如图13-1所示，这5个神经元的局部接受域由5个虚线表示）。不同神经元的局部接受与可能部分重叠，放在一起就构成了整个视野。此外，作者指出一些神经元只对水平线感兴趣，而另一些只对线的不同方向做出反应。他们也注意到，一些神经元具有较大的接受域，只会对由低级模式组合成的高级模式做出反应。这些观察结果带来了这样一个理念：高级神经元只以临近的低级神经元为基础（如图13-1，高层神经元只与部分地层神经元连接）。这一强大的结构可以检测到视觉领域的各种复杂模式。

 

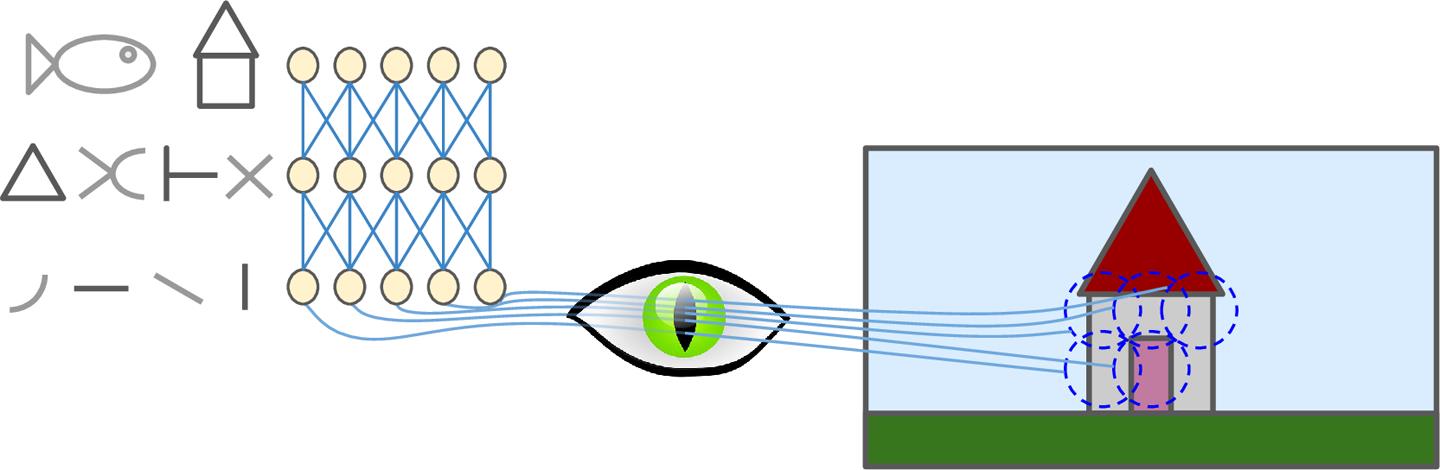
图13-1 视觉皮层的局部接受域

关于视觉皮层的研究激发了神经认知机（neocognitron，1980年引入），并逐步演变成如今的卷积神经网络。重要的里程碑是1998年的一篇论文，介绍了著名的LeNet-5架构，并广泛应用于手写数字识别。该架构的一些模块我们已经了解了，比如全连接和sigmoid激活函数，但是还要一些新的模块：卷积层（convolutional layers）和池化层（pooling layers）。

你也许会有疑问，为什么不用常规的全连接深度神经网络来完成常规的图像识别任务呢？不幸的是，它虽然对小图片（比如MNIST）表现良好，但对于高清大图就无能为力了。例如，一个$100 \\times 100$图片具有10000像素，即使第一个隐层只有1000神经元（已经极大地减少了传递给下层的信息），这意味仅仅是第一个隐层就会带来一千万的连接。而CNNs会通过使用部分连接层来解决这一问题。

13.2 卷积层

CNN最重要的构件就是卷积层（卷积是一种数学运算，度量两个函数乘积的逐点积分。其与傅里叶变换与拉普拉斯变换高度相关，在信号处理中应用广泛。卷积层实际上使用了互相关，这与卷积是相似的。卷积处理的是连续变量，互相关好像是离散变量。）：第一个卷积层的神经元并不和所有的输入全连接，只与其接受域的像素点连接（如图13-2）。依次的，第二个卷积层也与第一个卷积层部分相连。这一架构使得第一个隐层专注于低级别特征，然后在随后的隐层中将低级别特征进行组合。

图13-2 矩形局部接受域的CNN层

此前的神经网络处理的都是1D数据，而现在处理的是2D数据，这使得神经元更容易匹配到与其相关的输入。

位于第$i$行第$j$列的神经元，与之相连的前层神经元是$i$到$i + f_w - 1$行，$j$到$j + f_h - 1$列。其中，$f_h$和$f_w$是接受域的高和宽（如图13-3）。为了使两层的高和宽保持一致，需要在输入层的周围补零，这被称作零填充（zero padding）。

 

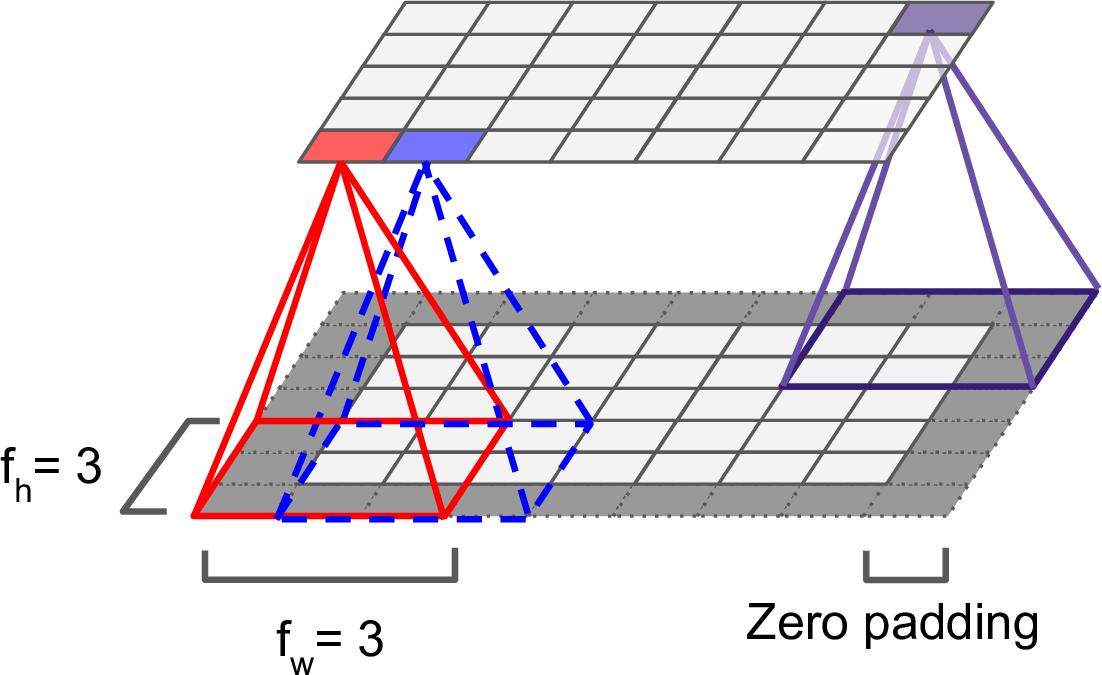
图13-3 卷积层连接，以及零填充

通过将接受域隔行划分，可以使得高层的尺寸小于底层，如图13-4。两个连续接受域的距离称为跨度（stride）。一个$5 \\times 7$的输入层连接一个$3 \\times 4$的高层，接受域为$3 \\times 3$，跨度为2（在这个例子中，两个方向的跨度是一样的，这也可以不一样）。与一个位于$i$行$j$列的高层神经元连接的是$i \\times s_w$到$i \\times s_w + f_w - 1$行，$j \\times s_h$到$j \\times s_h + f_h - 1$列的低层神经元。其中，$s_w$和$s_h$是水平跨度和垂直跨度。

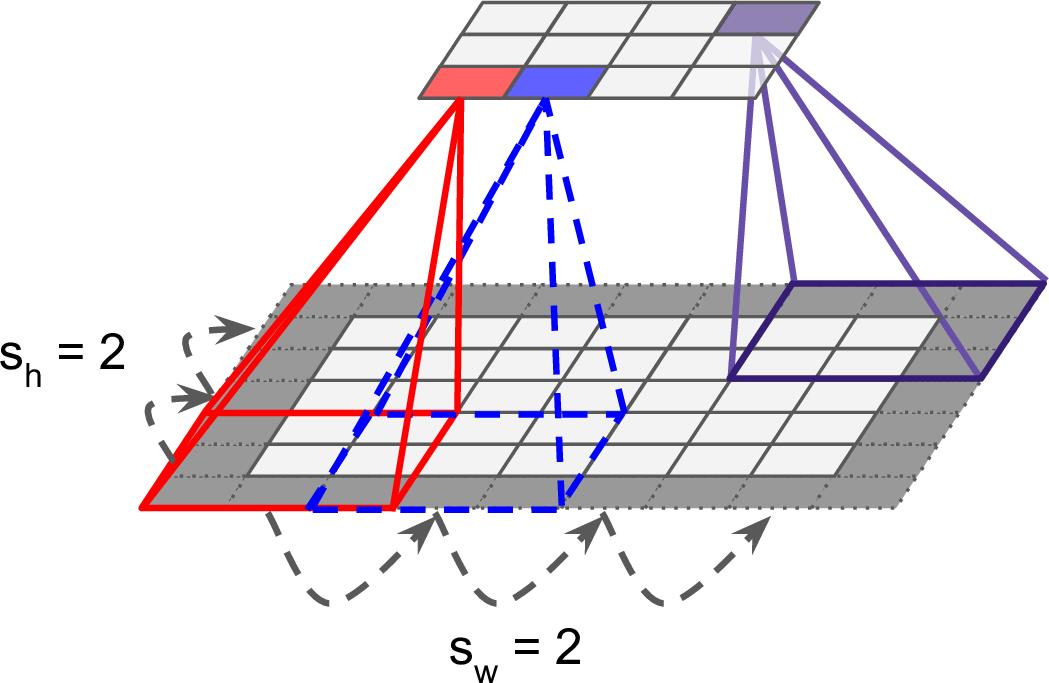
图13-4 通过跨度降维

13.2.1 过滤器

 神经元的权重可以表示接受域内的一个小的影像。例如，图13-5展示了两套可能的权重，称作过滤器（或者卷积核）。第一个过滤器描绘了一个在正中间拥有白色直线的黑块（这是一个$7 \\times 7$的矩阵，除了中间那条竖线是1之外，其他地方都是0）。神经元使用这样的权重，只会注意到其接受域中间的那条竖线，而忽视其他像素点。第二个过滤器是同样大小的黑块，但中间是条白色的水平线。神经元使用这样的权重，只会注意到其接受域中间的那条直线。

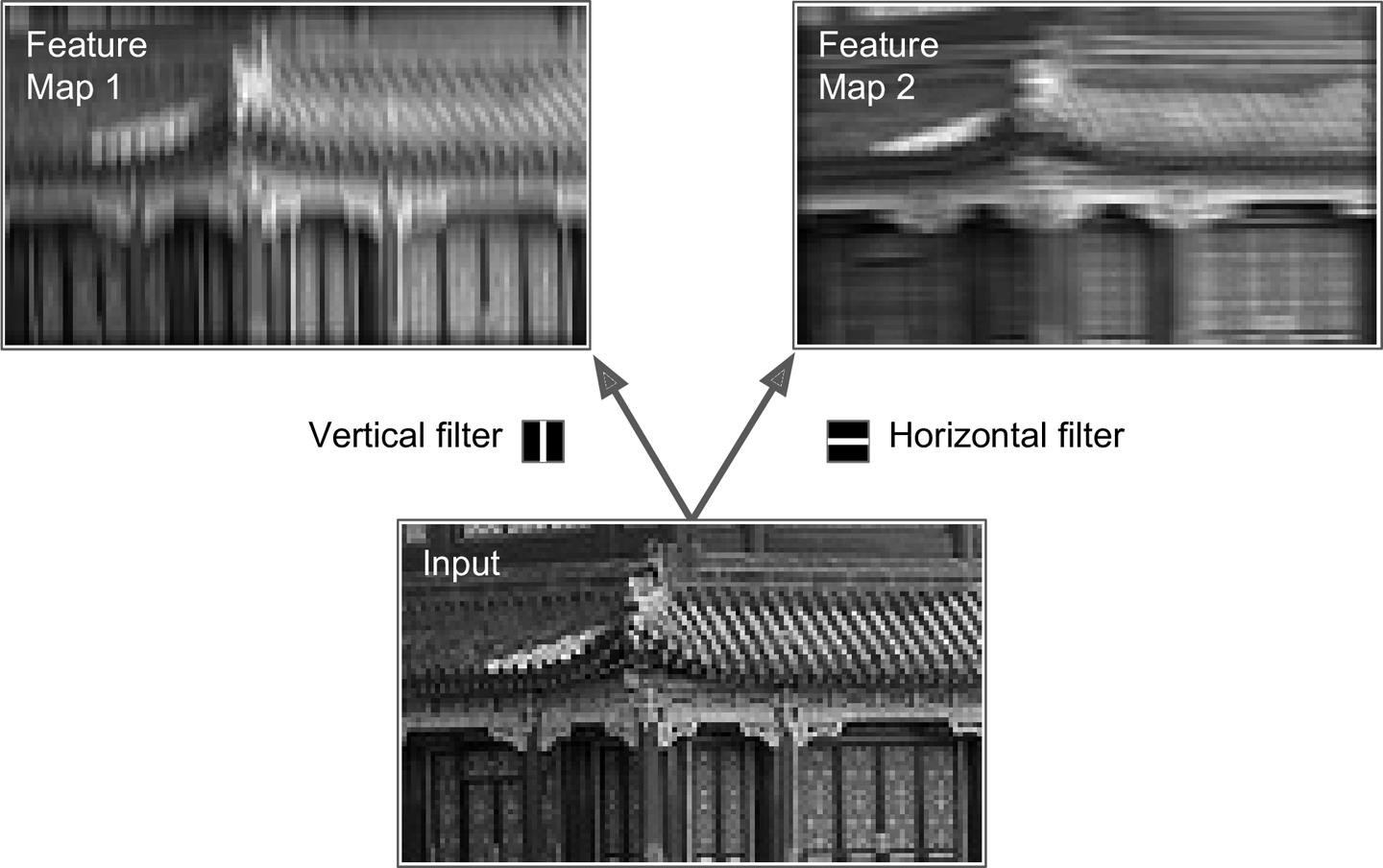
图13-5 应用两种不同的过滤器来获取特征图

如果一层的神经元使用同样的垂线过滤器（偏置项也一致），输入是图13-5底部的图像，将会输出左上角的图像。相似的，如果使用水平线过滤器，将会得到右上角的图像，可以看到，水平线增强了，其他部分变模糊了。因此，一层神经元使用同样的过滤器，可以得到一个特征图（feature map），将图像中与过滤器最相似的部分凸显出来。在训练过程中，一个CNN根据其任务存在最有用的过滤器，然后学着将其组合成更复杂的模式。

13.2.2 堆叠多重特征图（Stacking Multiple Feature Maps）

当目前为止，为了简单起见，我们将每个卷积层都表示为了简单的2D层。事实上，它是由许多大小相同的特征图组成，因此用3D表示一个卷积层更精确（如图13-6）。在一个特征图中，所有神经元共享同样的参数（权重和偏置），不过不同的特征图有不同的参数。神经元的接受域与之前的描述相同，但是被扩展到了前层的所有特征图。简而言之，一个卷积层会将多重过滤器同时应用于输入，以便检测输入中任何地方的多重特征。

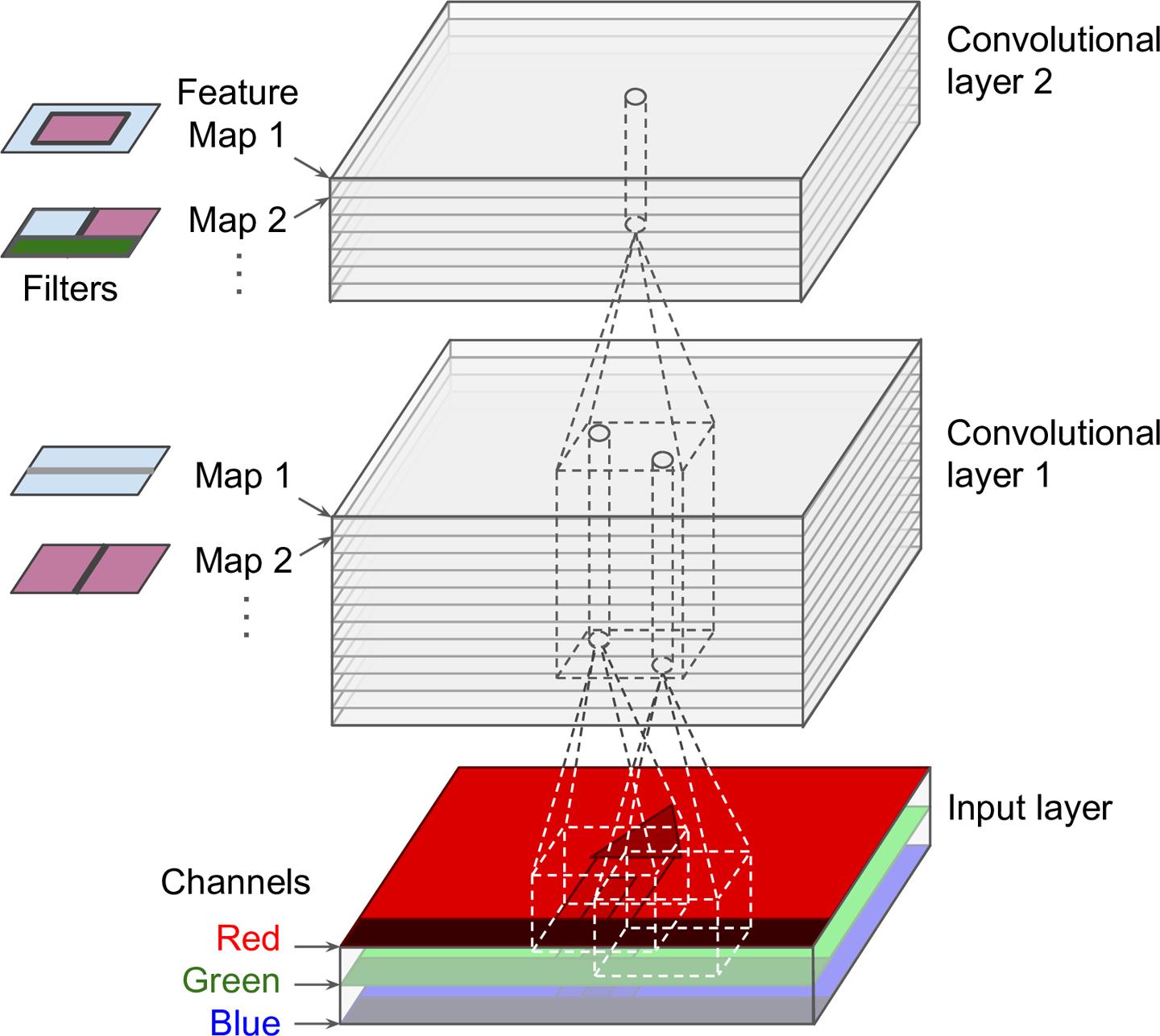
图13-6 卷积层有多个特征图，图像有三个通道

由于一个特征图的所有神经元共享同样的参数，这显著地降低了模型的参数数量。更重要的是，这意味着CNN在一个地方识别出来一种模式，还能在其他地方识别出这一模式。相反，一个普通的DNN在一个地方识别出了一种模式，它这能在这个特定的地方识别这一模式。

此外，输入图像也可能都多个子层组成：一个颜色通道一个子层。灰度图只用一个通道，但是有个图可以有更多的通道——例如，卫星图像可以捕捉到额外的光频率（比如红外线）。

具体的，对于第$l$个卷积层的第$k$个特征图的第$i$行$j$列的神经元，与之连接的底层（$l-1$层）神经元位于$i \\times s_w$到$i \\times s_w + f_w - 1$行，$j \\times s_h$到$j \\times s_h + f_h - 1$列，穿过所有的特征图（$l-1$层中的）。第$l$层中位于不同特征图的第$i$行$j$列神经元连接的是完全相同的前层神经元的输出。

一个卷积层一个神经元的计算公式：

\\begin{align*}
z_{i,j,k} = b_k + \\sum_{u=1}^{f_h}\\sum_{v=1}^{f_w}\\sum_{k\'=1}^{f_{n\'}} x_{i\',j\',k\'} \\cdot w_{u,v,k\',k}
\\end{align*}

需要注意的是，求和的时候并没有$i$和$j$。每一个特征图使用的权重是一样的。所以这不仅仅是第$i$行$j$列神经元的输出，并没有特指是哪个神经元的输出，而是第$l$层第$k$个特征图中每个神经元输出的计算公式。理解公式时，我们忽略$i$和$j$即可。

其中，

• $i\' = u \\cdot s_w + f_w - 1$
• $j\' = v \\cdot s_h + f_h - 1$
• $z_{i,j,k}$是第$l$卷积层第$k$个特征图，第$i$行$j$列神经元的输出。
• $s_h$和$s_w$分别是垂直和水平跨度，$f_h$和$f_w$分别是接受域的高和宽，$f_{n\'}$是前层特征图的个数（$l-1$层）。
• $x_{i\',j\',k\'}$是第$l-1$层，第$k\'$个特征图（如果前层是输入层，那就是第$k\'$个通道），第$i\'$行$j\'$列神经元的输出。
• $b_k$是第$l$层第$k$个特征图的偏置项。可以把它看做一个开关，来调整第$k$个特征图的整体亮度。
• $w_{u,v,k\',k}$是第$l$层第$k$个特征图中的任意一个神经元，它的第$k\'$个特征图的第$u$行第$v$列的输入的权重。

13.2.3 TensorFlow实现

相关代码可参考本书代码

在TensorFlow中，每个输入图像都被表示成形状为[height, width, channels]的3D张量。一个mini-batch表示成形状是[mini-batch size, height, width, channels]的4D张量。卷积层的权重表示成形状为$[f_h, f_w, f_n, f_{n\'}] $的4D张量。卷积层偏置表示成形状为$[f_n]$的1D张量。

我们来看一个简单的例子。下面代码首先使用Scikit-Learn的load_sample_images()加载两幅图像。然后创建两个$7 \\times 7$的过滤器（与图13-5相同），然后通过一个卷积层将这两个过滤器应用于两幅图，该卷积层有TensorFlow的conv2d()函数创建（包括0填充和大小为2的跨度）。最后绘制了其中的一个卷积层。

import numpy as np
from sklearn.datasets import load_sample_images

# 加载两个图片
dataset = np.array(load_sample_images().images, dtype=np.float32)
batch_size, height, width, channels = dataset.shape

# 创建两个过滤器
filters_test = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters_test[:, 3, :, 0] = 1 # 垂线
filters_test[3, :, :, 1] = 1 # 水平线

# 创建一个图，包括输入X和使用了两个过滤器的一个卷积层。
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
convolution = tf.nn.conv2d(X, filters, strides=[1,2,2,1], padding="SAME")

with tf.Session() as sess:
    output = sess.run(convolution, feed_dict={X: dataset})

plt.imshow(output[0, :, :, 1]) # 绘制第一幅图的第二个特征图
plt.show()　　

关于conv2d()函数的一些说明：

• X是mini-batch输入（一个4D张量，如前所示）
• filters是一个过滤器集（4D张量，如前所示）
• strides拥有4个元素的一维数组，中间两个元素表示垂直和水平跨度。第一和第四个元素目前直接设置为1。以后可能会用来表示批跨度（跳过一些实例），以及通道跨度（跳过先前层的一些通道或者特征图）。
• padding有"VALID"、"SAME"两个选择：
  • 如果设置为"VALID"，卷积层不使用0填充，可能会直接忽略边缘的一些输入，如图13-7所示（为简单起见，图中只显示了中间的水平线）。
  • 如果设置为"SAME"，卷积层在必要的时候使用0填充。

图13-7 填充选项——输入宽度：13，过滤器宽度：6，跨度：5

不幸的是，卷积层有许多超参数需要调整。必须选择它们的过滤器数量，以及高、宽、跨度、填充类型。可以用网格搜索选择超参数，但这比较耗时。在随后介绍CNN架构师，会给出超参数选择的一些最佳实践。

13.2.3 内存要求

CNN的另一个问题是卷积层需要使用大量的RAM，尤其是训练的时候，因为反向传播需要前向传递的所有中间值。

比如，考虑一个卷积层，过滤器的形状是$5 \\times 5$，需要输出形状为$150 \\times 100$的200个特征图（需要使用200个过滤器），其中跨度为1，padding选择SAME。如果输入是一个$150 \\times 100$的RGB图像（3个通道），那么参数的个数就是$(5 \\times 5 \\times 3 + 1) \\times 200 = 15200$（+1是由于偏置项），这一数字已经远小于全连接了。但由于200个特征图中的每一个都包含$150 \\times 100$个神经元，计算每个神经元的输出时都要用权重乘以$5 \\times 5 \\times 3 = 75$个输入然后再加和：这总共是2.25亿次浮点乘法运算。此外，如果用32-bit浮点数表示特征图，这个卷积层输出占据RAM的空间将达到200 × 150 × 100 × 32 = 96百万比特（大约11.4 MB）。而这仅仅是一个样本。如果这个训练批次有100个样本，这一层将会使用超过1G的RAM。

进行预测时，只要一层计算完毕，其前层就可以释放掉。因此所需的RAM只要能容纳连个连续层即可。但是在训练时，每层前向传播的输出都要保留下来，以便用于反向传播时计算梯度。此时所需的RAM至少可以存储所有层的输出。

如果训练时内存溢出，可以减小mini-batch的大小。此外，也可以通过增大跨度，或者减少层级。或者使用16-bit浮点数代替32-bit浮点数。也可以分布式训练。

13.3 池化层（Pooling Layer）

池化层的目标是通过二次抽样，来减少计算量、内存使用、参数数量（降低了过拟合的风险）。降低图像尺寸也使得模型可以忍受一点点图像移位。和卷积层一样，池化层也只和前层的部分神经元连接，同样是一个矩形接受域。也需要定义接受域的尺寸、跨度、填充类型。不过，一个池化神经元没有权重，仅仅是使用诸如max、mean的聚合函数对输入进行聚合。 图13-8展示了一个max池化层，这是最常见的池化层。在这例子中，使用了2 × 2池化核，跨度2，无填充。只用每个核的最大输入才会传递给下一层，其他的输入被丢弃掉。

图13-8 Max池化层（2 × 2池化核，跨度2，无填充）

很明显，每个方向的输出的尺寸都只有输入的一半（面积只有1/4），丢掉了输入值的75%。

池化层一般独立地工作于每个输入通道，因此输出深度和输入深度是一样的。随后我们会越高一些通道，在这种情形下图像的空间维度不变（宽和高），但是通道会减少。

TensorFlow实现：

[...] # load the image dataset, just like above

# Create a graph with input X plus a max pooling layer
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
max_pool = tf.nn.max_pool(X, ksize=[1,2,2,1], strides=[1,2,2,1],padding="VALID")

with tf.Session() as sess:
    output = sess.run(max_pool, feed_dict={X: dataset})

plt.imshow(output[0].astype(np.uint8)) # plot the output for the 1st image
plt.show()

其中，ksize是一个四维张量，包含了每个维度池化核的形状[batch size, height, width, channels]。TensorFlow目前还不支持越过实例，因此ksize[0]必须是1。此外，也不支持同时越过空间维度（宽和高）和深度。因此，或者ksize[1]、ksize[2]同时为1，或者ksize[3]为1。

13.4 CNN架构

典型的CNN架构会堆叠一些卷积层（每个卷积层跟着ReLU层），然后是一个池化层，然后另外一些卷积层（+ReLU）， 然后再是池化层，等等。图像会越来越小，但一般也会越来越深（也就是更多的特征图）。在堆的最顶端，会有常规的全连接前向神经网络（+ReLUs），输出层输出概率（例如，对于图像分类问题，softmax层输出每个类别的概率）。

图13-9 典型的CNN架构

一个常见的错误是使用了尺寸太大的卷积核。堆叠两个3 × 3的卷积核，可以达到与一个9 × 9卷积核相似的效果，但前者的计算量小得多。

近年来，这一架构的变体逐渐成熟，并取得了巨大的成功。一个衡量标准就是在该类竞赛中错误率的降低。可以参考ILSVRC ImageNet challenge。

我们首先介绍一下经典的LeNet-5架构（1998），然后是ILSVRC挑战赛的三个获胜者：AlexNet (2012), GoogLeNet (2014)和ResNet(2015)。

其他的视觉任务：目标检测和定位，以及图像分割。在图像检测和定位中，这样网络一般会输出一系列包围盒，将不同的对象包围起来。例如，Maxine Oquab等人2015年的论文，输出每个对象类的热图（heat map）。Russell Stewart等人2015年的论文，使用CNN检测人脸，并使用RNN识别边界。对于图像分割，可参考这篇论文。

13.4.1 LeNet-5

LeNet-5是最广为人知的CNN架构。在1998年提出比广泛应用于手写数字识别（MNIST）。由以下各层组成：

其中，

• MNIST图像是28 × 28像素，0填充后是32 × 32像素，并且在输入之前进行标准化（normalized）。剩下的各层不再填充。
• 这里的平均池化层（average pooling layers）比常规的稍微复杂：每个神经元求出其输入均值后，要对该均值乘以一个可学习的系数（每个特征图一个系数）并加上一个可学习的偏置（也是每个特征图一个），然后将结果应用于激活函数。
• C3中的大部分神经元只与S2中的3到4个特征图连接，而不是全部的6个。
• 输出层也有一点特殊，具体可以看论文。

LeNet-5数字分类的demo，可参考Yann LeCun的网站（"LENET" 章节）。

---

后面的AlexNet (2012), GoogLeNet (2014)和ResNet(2015)有时间再补充吧。