顺序表的理解

Posted 2020-11-07 在这里, 意淫和实干都值得尊重

顺序表

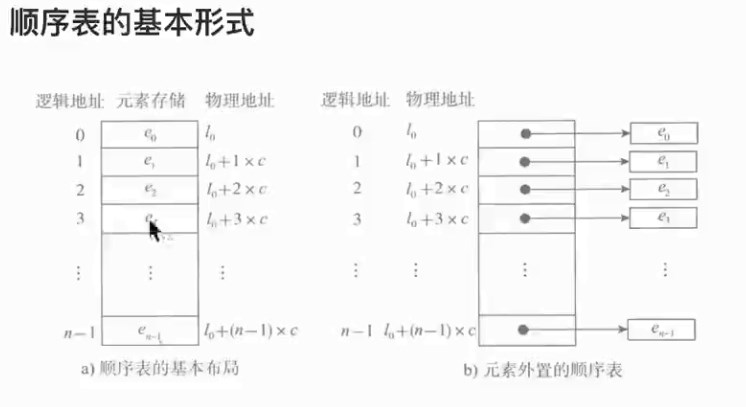
顺序表的基本形式

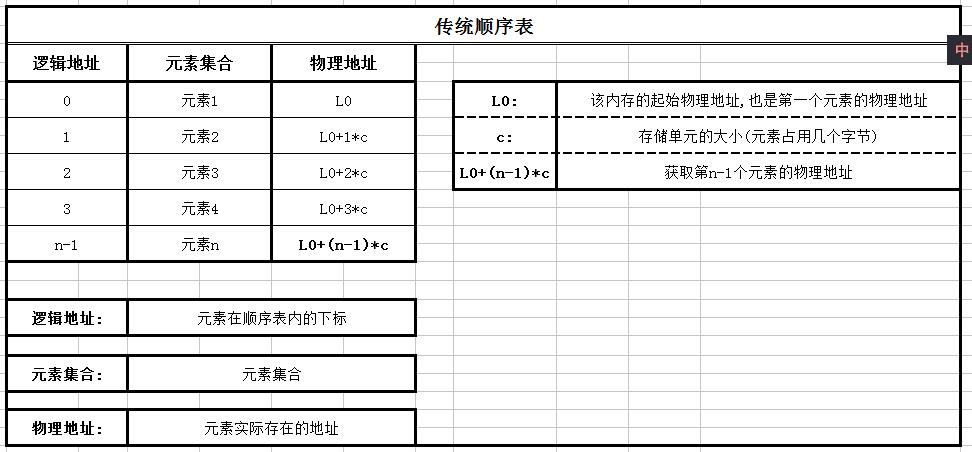
传统顺序表:

起始物理地址+逻辑地址(元素下标)*存储单元大小(每一个元素所占用几个字节)=所查找元素的物理地址

1. 数据元素本身连续存储,每个元素所占的存储单元大小固定相同
   
   
   1. 元素的下标是其逻辑地址,而元素存储的物理地址是元素实际内存地址
   2. 可以通过存储区起始地址加上逻辑地址与存储单元的大小(c)的乘乘积计算而得

   即:L0+(n-1)*c得到你想要的元素的物理地址

 

---

元素外置顺序表

背景: 存储数据类型不一样,导致存储单元大小不一样, 导致不能使用传统的顺序表来读写数据

元素外置

1. 各个元素对应自己的物理地址
   1. 将各个元素的物理地址以传统顺序表的形式存储起来
   2. 每次读写,只需要查找存放的顺序表内的(元素的物理地址)即可

顺序表的结构与实现

顺序表的结构:

1.表头信息
2.数据区

表头信息:

1. 容量(能存多少元素)
   1. 元素个数(当前存了多少个元素)

数据区:

元素集合

顺序表的两种基本形式

1.一体式结构:

描述:
存储表信息的单元与元素存储区以连续的方式安排在一块存储区内,两部分数据的整体形成一个完整的顺序表对象
特点:
一体式结构整体性强,易于管理,但是由于数据元素存储区是表对象的一部分,数据表创建后,元素存储区就固定了,
注意:
若存储区满了,再添加元素,则需要更改整个表对象

2.分离式结构:

1.表对象

表对象里只保存与整个表有关的信息
(容量和元素的个数)

2.元素集合

实际元素元素存放在另一个独立的元素存储区内
通过链接与基本表对象关联

元素存储区替换

1.一体式

一体式结构由于顺序表信息区与数据区连续存储在一起,
所以若想更改数据区,则只能整体搬迁
即整个顺序表对象(指存储在顺序表的结构信息的区域改变了)

2.分离式

只需要将表信息区中链接地址更新即可,而该书序对象不变

**主要采用分离式结构

元素存储区扩充

动态顺序表

采用分离式结构的顺序表,若将数据区更换为更大的存储空间,则可以不在改变表对象的前提下
对其数据区进行扩充,所有使用这个表的地方都不必修改
只要在程序的运行环境(计算机系统)还有空间存储,这种表结构就不会因为满了而导致操作无法进行
这种技术实现的顺序表称为动态顺序表
因为其容量可以在使用中动态变化

动态顺序表特征:

1. 不更改表对象
   1. 不更改表结构
   2. 只对其数据存储区进行修改

扩充的两种策略

1.线性增长:

每次扩充增加固定的存储位置
如:每次扩充增加10个元素位置
特点:节省空间,但扩充操作频繁(操作次数多)

2.加倍扩充

每次扩充容量加倍, 如每次扩充增加一倍的存储空间
特点:
减少了扩充的操纵次数,浪费空间资源

主要采用加倍扩充,[以空间换时间]

顺序表的操作

1.从头部插入

原列表内所有的元素全部后移一位
然后将新元素插入
时间复杂度为O(n)

2.从尾部插入

直接在尾部插入即可
时间复杂度为O(1)

[====以上为保序的情况====]

3.不保序

直接将要插入的位置的元素添加到队尾,将新元素插入到腾出来的位置
时间复杂度为O(1)

删除元素

1.尾部删除:

直接从尾部删除
时间复杂复为O(1)

2.其他位置删除:

直接删除元素,该元素后面的元素统一前移一位
时间复杂度为O(1)

[====以上为保序删除====]

3.非保序

将尾部的元素直接替换掉要删除的元素
时间复杂度为O(1)

Python中的list:

采用分离式技术实现的动态顺序表

python标准类型list就是一种元素个数可变的线性表
并在各种操作中维持已有元素的顺序(保序)
基于下标的高效元素访问和更新,时间复杂度为O(1)

允许任意加入元素,而且在不断假如元素的过程中,表对象的标识(函数id得到的值)不变

为满足该特征,就必须更换元素存储区,并且为保证更换存储区是list对象的标识id不变,只能采用分离式实现技术

在pytho的官方实现中,list就是一种采用分离式技术实现的动态顺序表

尾部添加比其他坐标插入效率高
list实现采用如下策略
在建立表时(或很小的表),系统分配一块能够容纳8个元素的存储区,在执行插入操作时,如果元素存储区满了, 就换一块4倍大的存储区
但如果此时的表已经很大(目前的阀值为50000)
则改变策略,采用加一倍的方法
避免出现过多的空闲的存储位置

<wiz_tmp_tag id="wiz-table-range-border" contenteditable="false" style="display: none;">