细解-动态规划
Posted 川山甲
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了细解-动态规划相关的知识,希望对你有一定的参考价值。

思路:通过假设法,寻找数据间的关系,进行建模。
假设n=4,穷举所有的切割方式,找到最佳的切割方案。
不切(0刀):最高9元
1刀:最高10元

2刀:最高7元

3刀:最高4元
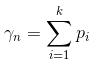
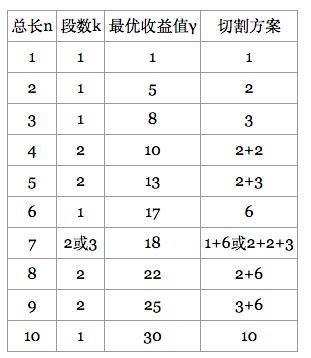
观察数据:(总长为5米的钢材最优收益是:2米刚才最优收益+3米钢材最优收益加和。)
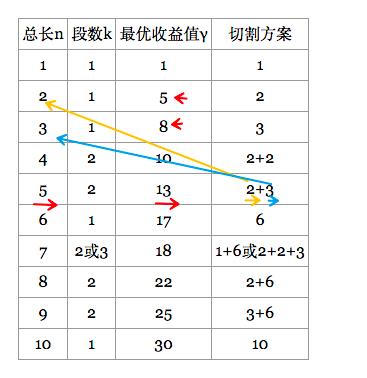
从上述表,我们可以得出:对于γn(n>= 1),我们可以用更短的钢条的最优切割收益来描述它:

对于每个i=1、2、...、n-1,方案步骤如下:
1)将钢条切割为长度为i和n-i的两段;
2)求解这两段的最优切割收益γi和γn-i。——每种方案的最优收益为两段的最优收益之和。
由于无法预知那种方案会获得最优收益,我们必须考察所有可能的i,选取其中收益最大者。
原有方式:

简化版本:钢条从左边切割下长度为i的一段,对左边的一段i不再进行切割,只对右边剩下的长度为n-i的一段继续进行切割(采用了一种自顶向下的递归方式)
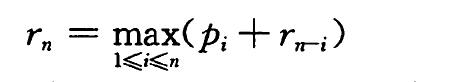
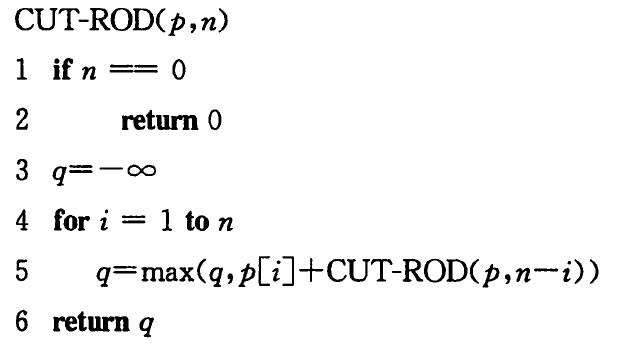
分析CUT-ROD:实际运行中,你会发现CUT-ROD的效率很差。因为CUT-ROD反复地用相同的参数值对自身进行递归调用,即它反复求解相同的子问题,如下图所示:
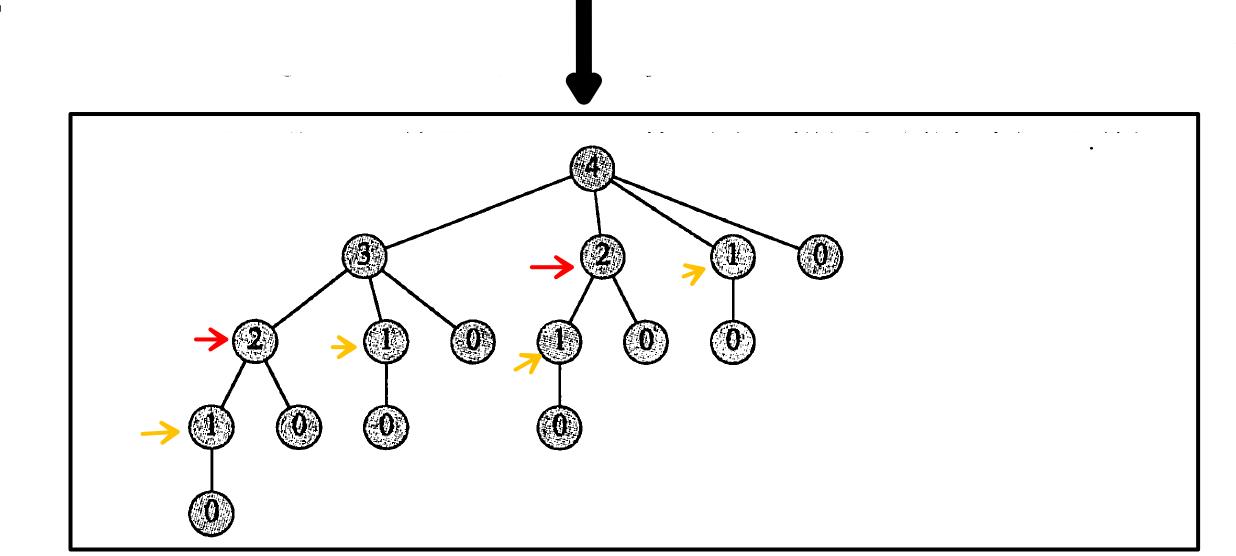
CUT-ROD的运行时间为n的指数,时间复杂度如下:
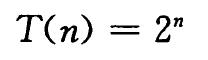
动态规划方法的核心思想是:对每个子问题只求解一次,并将结果保存下来。如果随后再次需要此子问题的解,只需查找保存的结果,而不必重新计算。因此,动态规划方法是付出额外的内存空间来节省计算时间,是典型的时空权衡的例子。
方法1:带备忘的自顶向下法。此方法扔按自然的递归形式编写,但过程会保存每个子问题的解(通常保存在数组或散列中)。当需要一个子问题解时,过程首先检查是否已保存过此解,无则计算,有则返回。

方法2:自底向上法。将子问题按规模排序,按由小至大顺序求解。当求解某个子问题时,它所依赖的那些更小的子问题都已求解完毕,结果已保存。每个子问题只需求解一次,当我们求解它时,它的所有前提子问题都已经求解完成。

当思考一个动态规划问题时,我们应该弄清所涉及的子问题及子问题之间的依赖关系。
上面举得n=4时,钢条切割问题的子问题图如下:这是递归调用树的简化版,树中标号相同的节点收缩为图中的单一顶点,所有边均从父节点指向子节点。
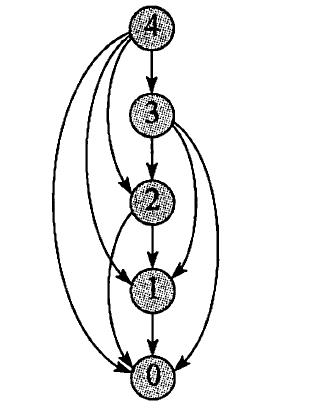
上面的图中,我们可以把每个顶点向量化,标记为(x,y)。这个表示求解x的问题时候,我们需要子问题y的解。

以上是关于细解-动态规划的主要内容,如果未能解决你的问题,请参考以下文章