MT193三面角的正余弦定理

Posted 2020-11-07 青春的记忆

(原题为浙江名校新高考研究联盟2018届第三次联考选择压轴题) 在平面$\\alpha$内，已知$AB\\perp BC$,过直线$AB,BC$分别作平面$\\beta,\\gamma$，使得锐二面角$\\alpha-AB-\\beta$为$\\dfrac{\\pi}{3}$，锐二面角$\\alpha-BC-\\gamma$为$\\dfrac{\\pi}{3}$，则平面$\\beta$和平面$\\gamma$所成的锐二面角的余弦值为____

(原题为浙江名校新高考研究联盟2018届第三次联考选择压轴题)

在平面$\\alpha$内，已知$AB\\perp BC$,过直线$AB,BC$分别作平面$\\beta,\\gamma$，使得锐二面角$\\alpha-AB-\\beta$为$\\dfrac{\\pi}{3}$，锐二面角$\\alpha-BC-\\gamma$为$\\dfrac{\\pi}{3}$，则平面$\\beta$和平面$\\gamma$所成的锐二面角的余弦值为____

提示:如图注意到以下结论：(三面角的第二余弦定理)$\\cos D=-\\cos A\\cos C+\\sin A\\sin C\\cos \\angle CBA$

其中$A,C,D$分别表示二面角$D-BA-C,D-BC-A,A-BD-C$所表示的二面角的平面角

此题中$\\alpha-AB-\\beta=C-AB-D；\\alpha-BC-\\gamma=A-BC-D$代入数值得$\\cos D=-\\cos\\dfrac{\\pi}{3}\\cos\\dfrac{\\pi}{3}=-\\dfrac{1}{4}$

由于所求为锐二面角，故答案为$\\dfrac{1}{4}$.

 

 

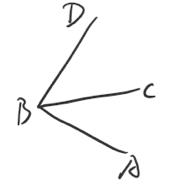
注:

1.三面角的正弦定理如图为:$\\dfrac{\\sin D}{\\sin\\angle CBA}=\\dfrac{\\sin C}{\\sin\\angle DBA}=\\dfrac{\\sin A}{\\sin\\angle CBD}$ 

2.三面角的第一余弦定理(三射线定理):$\\cos\\angle CBA=\\cos\\angle DBA\\cos\\angle DBC+\\sin\\angle DBA\\sin\\angle DBC\\cos D$

3.与这些类似的还有一个和线面角最小有关的三余弦定理.