线性链CRF

Posted 2020-11-07 弥漫的幻雪的博客

 

一、序列标注问题通用概率图结构

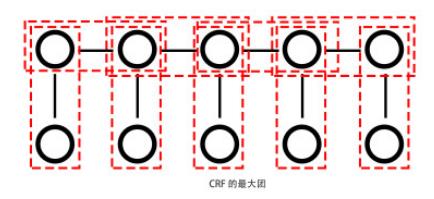
如图，对于序列标注问题，第一行的节点是标注标签，第二行是词。

例如“我 爱 美丽的 四川 九寨沟”

第一行节点分别是：代词、动词、形容词、名词、名词

第二行节点分别是：我、爱、美丽的、四川、九寨沟

所以模型的假设是：句子中，相邻词的词性是有逻辑关系的，每个词的词性和词性也是有关系的。词性是隐含的随机变量，词是表面的随机变量。

 

二、线性链假设的好处

CRF的条件概率分布是每个最大团的势函数的乘积。最大团的定义是，团中的节点两两之间都有连接，并且无法加入新的节点仍然保持团

如图，在线性链CRF中，第一行相邻的2个节点是最大团，有4个。每一列相邻的2个节点是最大团，有5个。所以上图可以拆分为9个最大团，即9个势函数的乘积。

由此，线性链CRF的好处，就是最大团的分解简单而规范化：只有2种最大团，相邻的隐层节点，如（代词，形容词），和每一对隐层节点和对应显层节点，如（代词，我）

 

三、势函数定义

每个最大团的势函数，就是对应特征函数的指数化。2种最大团对应2种特征函数：

转移特征函数tk对应相邻的隐层节点，所以它和yi-1,yi有关

状态特征函数sl对应每一对隐层和显层节点，所以它和yi,x有关

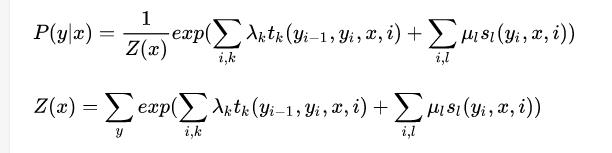
如图，指数相加，实际上是势函数的相乘。

 

四、参数学习

线性链CRF的参数学习，就是在学习每个势函数的权重值