二叉排序树

Posted 2020-11-07 O了吗

二叉排序树

定义

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

查找

若根结点的关键字值等于查找的关键字，成功。否则，若小于根结点的关键字值，递归查左子树。若大于根结点的关键字值，递归查右子树。若子树为空，查找不成功。

插入

首先执行查找算法，找出被插结点的父亲结点。

判断被插结点是其父亲结点的左、右儿子。将被插结点作为叶子结点插入。

若二叉树为空。则首先单独生成根结点。

注意：新插入的结点总是叶子结点。

删除

在二叉排序树删去一个结点，分三种情况讨论：

1.若*p结点为叶子结点，即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构，则可以直接删除此子结点。

2.若*p结点只有左子树PL或右子树PR，此时只要令PL或PR直接成为其双亲结点*f的左子树（当*p是左子树）或右子树（当*p是右子树）即可，作此修改也不破坏二叉排序树的特性。

3.若*p结点的左子树和右子树均不空。在删去*p之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整，可以有两种做法：

其一是令*p的左子树为*f的左/右(依*p是*f的左子树还是右子树而定)子树，*s为*p左子树的最右下的结点，而*p的右子树为*s的右子树；

其二是令*p的直接前驱（或直接后继）替代*p，然后再从二叉排序树中删去它的直接前驱（或直接后继）－即让*f的左子树(如果有的话)成为*p左子树的最左下结点(如果有的话)，再让*f成为*p的左右结点的父结点。

在二叉排序树上删除一个结点的图如下：

 

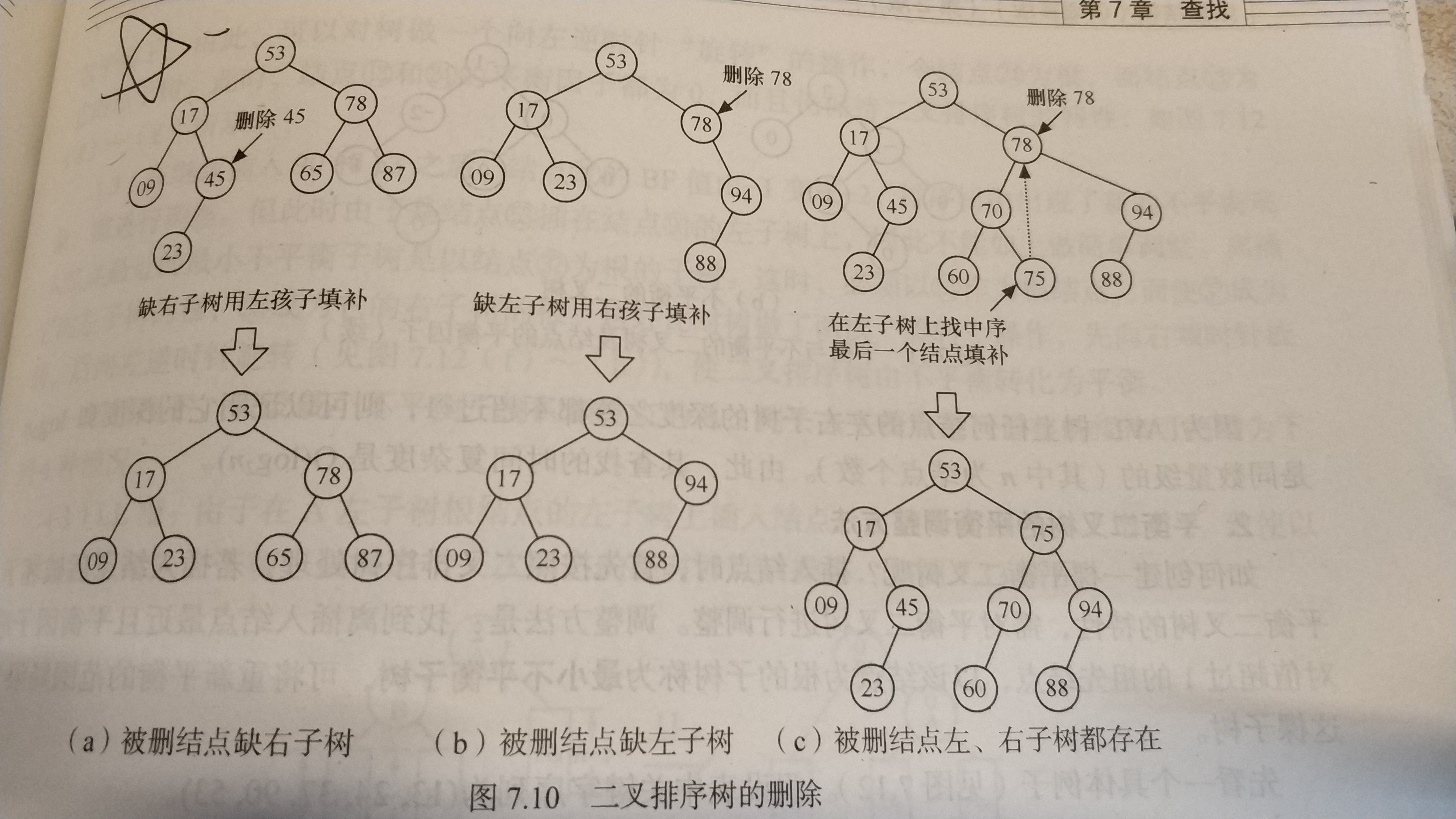
全部代码：

#include"iostream"
using namespace std;
typedef int element;
struct Tree{
    element data;
    Tree *left,*right;
};
//插入
void insert(Tree* &t,element data){
    if(!t){
        t = new Tree;
        t->data = data;
        t->left = NULL;
        t->right = NULL;
    }
    else if(data < t->data){
        insert(t->left,data);
    }
    else if(data > t->data){
        insert(t->right,data);
    }
}
//找查
Tree* find(Tree* &t,element key){
    if(!t || t->data == key){
        return t;
    }
    if(key < t->data){
        return find(t->left,key);
    }
    return find(t->right,key); 
}
//打印
void show(Tree* &t){
    if(t){
        show(t->left);
        cout<<t->data<<ends;
        show(t->right);
    }
}
//创建
void create(Tree* &t,element *a,int n){
    for(int i = 0;i < n;i++){
        insert(t,a[i]);
    }
}
//删除
int deleted(Tree* &t,element key){
    Tree *f = NULL,*p = t;        //f父节点与p删除节点
    //找到删除点p
    while(p){
        if(p->data == key){
            break;
        }
        f = p;
        if(key < p->data){
            p = p->left;
        }
        else{
            p = p->right;
        }
    }
    if(!p){        //未找到
        return 0;
    }
    Tree *q = p;
    //如果p有两个孩子
    if(p->right && p->left){
        Tree *s = q->left;
        while(s->right){
            q = s;
            s = s->right;
        }
        p->data = s->data;
        //删除s
        if(q == p){
            p->left = s->left;
        }
        else{
            q->right = s->left;
        }
        delete s;
        return 1;
    }
    //没有右孩子
    if(!p->right){
        q = p->left;
    }
    //没有左孩子
    else if(!p->left){
        q = p->right;
    }
    //要删除的点是根
    if(!f){
        t = q;
    }
    else{
        //在父结点左
        if(p == f->left){
            f->left = q;
        }
        //在父结点右
        else{
            f->right = q;
        }
    }
    delete p;
    return 1;
}
int main(){
    const int N = 11;
    Tree *t = NULL;
    int a[N] = {45,12,53,3,37,100,24,61,55,90,7};
    create(t,a,N);
    show(t);
    cout<<endl;
    deleted(t,3);
    show(t);
    //cout<<find(t,100)->data<<endl;         
    return 0;
}